【III積分】log x の積分を用いた練習問題にチャレンジ(東京都立大2016理学部第1問)

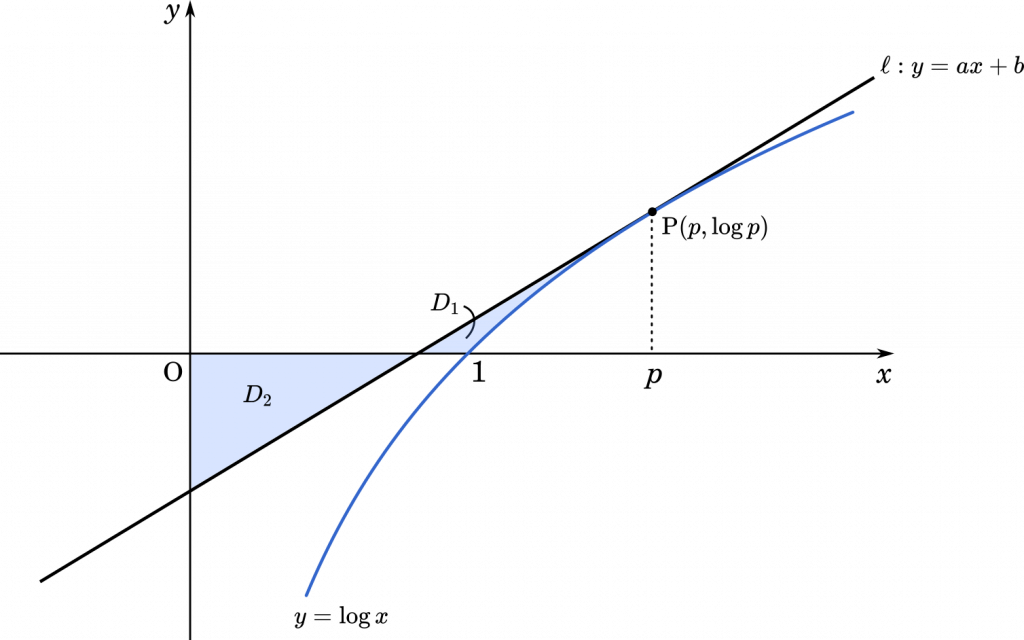
曲線 $y=\log x$ を $C$ で表す。$1<p<e$ をみたす実数 $p$ に対し，曲線 $C$ 上の点 P$(p,\log p)$ における接線を $\ell$ とし，$\ell$ の方程式を $y=ax+b$ とする。ただし，$\log x$ は自然対数とし，$e$ は自然対数の底とする。以下の問いに答えなさい。（東京都立大2016）

(1) $a$ を $p$ の式で表しなさい。

(2) $b$ を $p$ の式で表しなさい。

(3) $x$ 軸と直線 $\ell$ および曲線 $C$ で囲まれた図形 $D_1$ の面積を $p$ の式で表しなさい。

(4) $x$ 軸と $y$ 軸および直線 $\ell$ で囲まれた図形を $D_2$ とする。$D_1$ の面積と $D_2$ の面積が等しいとき，$p$ の値を求めなさい。

微分で接線の傾きを求める

(1)から始めます。

$y=\log x$ より
$y’=\cfrac{1}{x}$

これが接線の傾きになります。つまり，$x$ 座標が $p$ のときの傾きは $\cfrac{1}{p}$ です。

$a=\cfrac{1}{p}$ (答え)

切片を求める

(2)に進みます。今度は 1 次関数の切片を求めましょう。

$y=ax+b$ に $(p,\log p)$ と $a=\cfrac{1}{p}$ を代入して

$\log p=\cfrac{1}{p}\cdot p+b$
$\log p=1+b$
$b=\log p-1$　（答え）

log x の積分

(3)に進みます。

面積の求め方は，上の図のように三角形の面積から，$y=\log x$ と $x$ 軸，$x=p$ で囲まれた図形の面積を引くことで求められます。

三角形の底辺の長さを求めるために，直線と $x$ 軸との交点を調べましょう。

$\cfrac{1}{p}x+\log p-1=0$ として

$x+p\log p-p=0$

$x$ 軸との交点は

$x=p-p\log p$

よって，底辺の長さは

$p-p+p\log p=p\log p$

三角形の面積は

$\cfrac{1}{2}p\log p\cdot\log p$
$=\cfrac{1}{2}p(\log p)^2$

面積を求めます。

$\displaystyle D_1=\cfrac{1}{2}p(\log p)^2-\int_1^p \log x\space dx$

ここで，$\log x$ の積分のやり方をおさらいです。

$\log x$ を積分する公式はありません。そこで，$\log x$ は $(x)’$ を加えてムリヤリ部分積分に持ち込む，ということを暗記しておくことが大事です。

$\displaystyle\int_1^p (x)’\log x\space dx$

$\displaystyle=\Big[x\log x\Big]_1^p-\int_1^p x\cdot\cfrac{1}{x}\space dx$
$\displaystyle=\Big[x\log x\Big]_1^p-\int_1^p 1\space dx$
$\displaystyle=\Big[x\log x\Big]_1^p-\Big[x\Big]_1^p$
$=p\log p-1\cdot\log 1-p+1$
$=p\log p-p+1$

したがって

$D_1=\cfrac{1}{2}p(\log p)^2-p\log p+p-1$　（答え）

面積が一致する場合

(4)に進みます。

$D_2$ はただの三角形なので面積を簡単に求めることができます。ただし，三角形の高さの求め方に注意が必要です。グラフを見ると分かりますが，切片 $b=\log p-1$ はマイナスの値なので，このまま計算すると面積もマイナスの値になってしまいます。面積を求めるときには，符号を逆にしておきます。

$D_2=\cfrac{1}{2}(p-p\log p)(1-\log p)$
$=\cfrac{1}{2}p(1-\log p)(1-\log p)$
$=\cfrac{1}{2}p(1-\log p)^2$

$D_1=D_2$ とすると

$\cfrac{1}{2}p(\log p)^2-p\log p+p-1=\cfrac{1}{2}p(1-\log p)^2$
$=\cfrac{1}{2}p\{1-2\log p+(\log p)^2\}$
$=\cfrac{1}{2}p-p\log p+\cfrac{1}{2}p(\log p)^2$

よって，$\log p$ の項がキレイに消去できます。

$p-1=\cfrac{1}{2}p$
$2p-2=p$
$p=2$　（答え）