【IIBベクトル】球の表面上の点に引いた直線と点の距離を考える(東京都立大2015理学部第2問)

座標空間に 3 点 O($0,0,0$)，A($0,2,2$)，B($3,-1,2$) がある。三角形 OAB の周上または内部の点 P は AP = $\sqrt{2}$，$\overrightarrow{\text{OP}}\perp\overrightarrow{\text{AP}}$ を満たしているとする。このとき，以下の問いに答えなさい。（東京都立大2015）

(1) 点 P の座標を求めなさい。

(2) 三角形 OBP の面積を求めなさい。

(3) 点 Q が点 A を中心とする半径 $\sqrt{2}$ の球面上を動くとき，点 B から直線 OQ に引いた垂線の長さの最小値を求めなさい。

三角形の円周または内部の点

(1)から始めます。

三角形の周上または内部の点の場合は

$0\leqq s+t\leqq1$，$s\geqq0$，$t\geqq0$

です。

入試問題において，$s+t$ の定義は解答自体にあまり関係ないことも多いのですが，きちんと記述できるようになりましょう。

$\overrightarrow{\text{OP}}=s\overrightarrow{\text{OA}}+t\overrightarrow{\text{OB}}$ $(0\leqq s+t\leqq1,s\geqq0,t\geqq0)$　とする

問題文に $\overrightarrow{\text{OP}}$ と $\overrightarrow{\text{AP}}$ が出てくるので，$\overrightarrow{\text{AP}}$ を作ってみましょう。

$\overrightarrow{\text{AP}}=\overrightarrow{\text{OP}}-\overrightarrow{\text{OA}}$ より

$=s\overrightarrow{\text{OA}}+t\overrightarrow{\text{OB}}-\overrightarrow{\text{OA}}$
$=(s-1)\overrightarrow{\text{OA}}+t\overrightarrow{\text{OB}}$

$\overrightarrow{\text{OP}}\perp\overrightarrow{\text{AP}}$ より

$\overrightarrow{\text{OP}}\cdot\overrightarrow{\text{AP}}=0$
$\overrightarrow{\text{OP}}\cdot\overrightarrow{\text{AP}}=(s\overrightarrow{\text{OA}}+t\overrightarrow{\text{OB}})\cdot\{(s-1)\overrightarrow{\text{OA}}+t\overrightarrow{\text{OB}}\}$
$=(s^2-s)|\overrightarrow{\text{OA}}|^2+st\overrightarrow{\text{OA}}\cdot\overrightarrow{\text{OB}}+(s-1)t\overrightarrow{\text{OA}}\cdot\overrightarrow{\text{OB}}+t^2|\overrightarrow{\text{OB}}|^2$

ここで

$|\overrightarrow{\text{OA}}|^2=0^2+2^2+2^2=8$
$|\overrightarrow{\text{OB}}|^2=3^2+(-1)^2+2^2=14$
$\overrightarrow{\text{OA}}\cdot\overrightarrow{\text{OB}}=0\cdot3+2(-1)+2\cdot2=2$

よって

$\overrightarrow{\text{OP}}\cdot\overrightarrow{\text{AP}}=8(s^2-s)+2st+2(s-1)t+14t^2$
$=8s^2-8s+2st+2st-2t+14t^2$
$=8s^2-8s+4st-2t+14t^2=0$
$4s^2-4s+2st-t+7t^2=0$ ・・・①

次に，問題文の AP=$\sqrt{2}$ から式を作りましょう。

$|\overrightarrow{\text{AP}}|=\sqrt{2}$ の両辺を 2 乗して

$|\overrightarrow{\text{AP}}|^2=2$
$|\overrightarrow{\text{AP}}|^2=\{(s-1)\overrightarrow{\text{OA}}+t\overrightarrow{\text{OB}}\}^2$
$=(s-1)^2|\overrightarrow{\text{OA}}|^2+2(s-1)t\overrightarrow{\text{OA}}\cdot\overrightarrow{\text{OB}}+t^2|\overrightarrow{\text{OB}}|^2$
$=8(s-1)^2+4(s-1)t+14t^2=2$
$8s^2-16s+8+4st-4t+14t^2=2$
$8s^2-16s+4st-4t+14t^2+6=0$
$4s^2-8s+2st-2t+7t^2+3=0$ ・・・②

①と②を連立します。

①－②

$4s+t-3=0$ ・・・③

移項して

$4s+t=3$

両辺を 2 乗して

$16s^2+8st+t^2=9$
$16s^2+8st=9-t^2$
$4s^2+2st=\cfrac{9-t^2}{4}$ ・・・④

また③より

$4s=3-t$ ・・・⑤

④と⑤を，①に代入して

$\cfrac{9-t^2}{4}-3+t-t+7t^2=0$
$\cfrac{9-t^2}{4}-3+7t^2=0$

$9-t^2-12+28t^2=0$
$27t^2=3$
$t^2=\cfrac{1}{9}$

$t>0$ より

$t=\cfrac{1}{3}$

⑤に代入して

$4s=3-\cfrac{1}{3}=\cfrac{8}{3}$
$s=\cfrac{2}{3}$

これで，$s,t$ の値が分かったので，最初の式に代入していきます。

$\overrightarrow{\text{OP}}=s\overrightarrow{\text{OA}}+t\overrightarrow{\text{OB}}$
$\overrightarrow{\text{OP}}=\cfrac{2}{3}(0,2,2)+\cfrac{1}{3}(3,-1,2)$
$=(1,1,2)$　（答え）

ベクトルと三角形の面積

(2)に進みます。

三角形の面積は公式を使うと良いでしょう。

この公式は教科書によって載っているものと載っていないものがありますが，その割には実際の入試問題で使う機会が多いので，必須項目として覚えたほうが良いでしょう。

三角形 OBP の面積は

$S=\cfrac{1}{2}\sqrt{|\overrightarrow{\text{OB}}|^2|\overrightarrow{\text{OP}}|^2-(\overrightarrow{\text{OB}}\cdot\overrightarrow{\text{OP}})^2}$

(1)より

$|\overrightarrow{\text{OB}}|^2=14$
$|\overrightarrow{\text{OP}}|^2=1^2+1^2+2^2=6$

また

$\overrightarrow{\text{OB}}\cdot\overrightarrow{\text{OP}}=3\cdot1+(-1)\cdot1+2\cdot2=6$

だから

$S=\cfrac{1}{2}\sqrt{14\cdot6-6^2}$
$=\cfrac{1}{2}\cdot4\sqrt{3}$
$=2\sqrt{3}$　（答え）

垂線の長さの最小を求める

(3)に進みます。

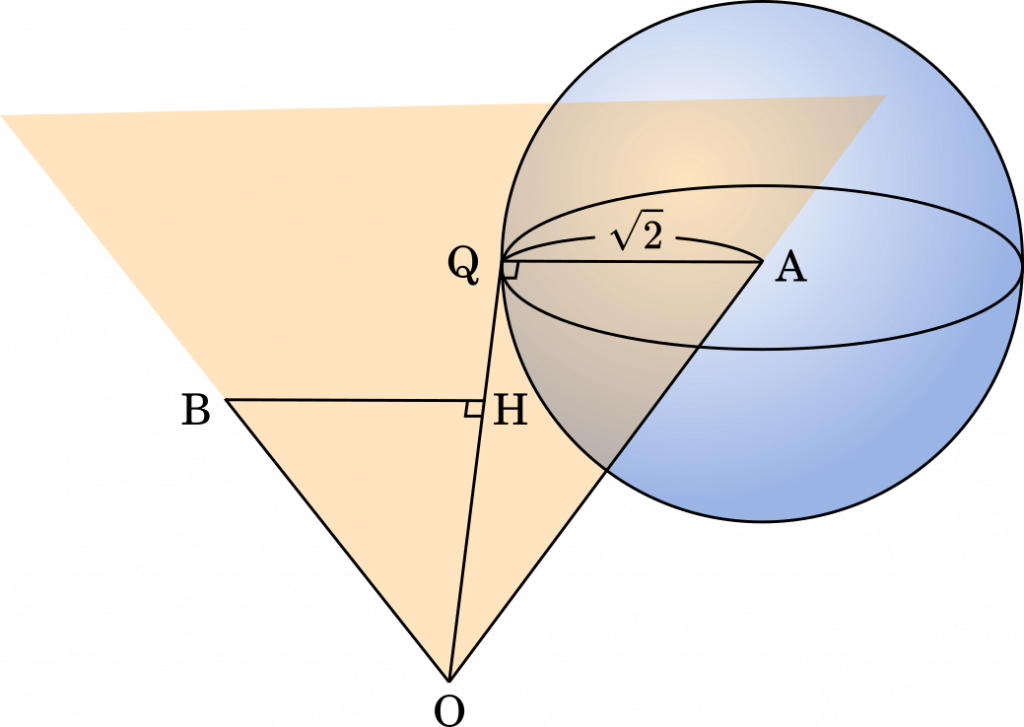
この問題はある程度想像力が必要です。数学的にキチンと説明すると話がかなりやっかいになるので，ここはイメージで捉えていきましょう。

点 B から直線 OQ に引いた垂線の足を H として，BH の長さが最小になる場合を考えてみます。

まず，点 Q が三角形 OAB のつくる平面上にある場合に BH が短くなります。

それをもとに，今度は点 Q が点 A を中心とする半径 $\sqrt{2}$ の円周上に存在すると考えます。

結局，BH が最も短くなるのは上のような状態のときです。このとき，点 Q は点 P と同じ点となります。

$\overrightarrow{\text{OH}}=k\overrightarrow{\text{OP}}$ として

$\overrightarrow{\text{OH}}=\overrightarrow{\text{OB}}+\overrightarrow{\text{BH}}$
$\overrightarrow{\text{BH}}=\overrightarrow{\text{OH}}-\overrightarrow{\text{OB}}$
$=k\overrightarrow{\text{OP}}-\overrightarrow{\text{OB}}$
$|\overrightarrow{\text{BH}}|^2=k^2|\overrightarrow{\text{OP}}|^2-2k\overrightarrow{\text{OB}}\cdot\overrightarrow{\text{OP}}+|\overrightarrow{\text{OB}}|^2$

ここで，(1)，(2)より $|\overrightarrow{\text{OB}}|^2=14$，$|\overrightarrow{\text{OP}}|^2=6$ であり，また
$\overrightarrow{\text{OB}}\cdot\overrightarrow{\text{OP}}=3\cdot1-1\cdot1+2\cdot2=6$

よって

$|\overrightarrow{\text{BH}}|^2=6k^2-12k+14$

式を平方完成すると

$=6(k^2-2k)+14$
$=6(k-1)^2-6+14$
$=6(k-1)^2+8$

よって，$|\overrightarrow{\text{BH}}|$ が最小となるのは $k=1$ のとき。

つまり，$\overrightarrow{\text{OH}}=\overrightarrow{\text{OP}}$ となるので，正しい図は以下です。

したがって，$|\overrightarrow{\text{BH}}|$ の最小値は

$|\overrightarrow{\text{BH}}|^2=\sqrt{8}$ より

$|\overrightarrow{\text{BH}}|=2\sqrt{2}$　（答え）

この問題は理屈を考えると難しい部分があるのですが，BH が最も短くなるとき，点 P と 点 Q が同じものになることさえ気づけば，計算自体はそれほどやっかいなものではありません。三次元の中で直線を移動させる想像力を鍛えましょう。