球面と直線および平面との共有点を求める(横浜国立大2018理系第2問)

O を原点とする $xyz$ 空間に点 A$(2,0,-1)$，および，中心を点B$(0,0,1)$とする半径 $\sqrt{2}$ の球面 $S$ がある。平面 $z=0$ 上の点P$(a,b,0)$ を考える。次の問いに答えよ。

(1) 直線 AP 上の点 Q に対して $\overrightarrow{\text{AQ}}=t\overrightarrow{\text{AP}}$ と表すとき，$\overrightarrow{\text{OQ}}$ を $a,b,t$ を用いて表せ。

(2) 直線 AP が球面 $S$ と共有点をもつとき，点 P の存在範囲を $ab$ 平面上に図示せよ。

(3) 球面 $S$ と平面 $x=-1$ の共通部分を $T$ とする。直線 AP が $T$ と共有点をもつとき，点 P の存在範囲を $ab$ 平面上に図示せよ。

ベクトル方程式

(1)から始めます。

ここは値を代入していくだけです。

$\overrightarrow{\text{AQ}}=t\overrightarrow{\text{AP}}$
$\overrightarrow{\text{OQ}}-\overrightarrow{\text{OA}}=t(\overrightarrow{\text{OP}}-\overrightarrow{\text{OA}})$
$\overrightarrow{\text{OQ}}=\overrightarrow{\text{OA}}+t(\overrightarrow{\text{OP}}-\overrightarrow{\text{OA}})$

$=(2,0,-1)+t(a-2,b,1)$
$=((a-2)t+2,bt,t-1)$　（答え）

球面と直線の共有点

数IIBでベクトルを習うときに，球面の方程式というものを習います。

球面 $S$ は

$x^2+y^2+(z-1)^2=(\sqrt{2})^2$

これが点 Q と共有点をもつので，(1)で求めた点 Q の座標を代入します。

$\{(a-2)t+2\}^2+(bt)^2+(t-1-1)^2=2$
$(a-2)^2t^2+4(a-2)t+4+b^2t^2+t^2-4t+4=2$
$\{(a-2)^2+b^2+1\}t^2+4(a-3)t+6=0$

ここは，判別式を用いれば $t$ を消去できます。

共有点をもつということは，$t$ が実数解をもつということです。よって，判別式の条件は $D\geqq0$ ということになります。

$\cfrac{D}{4}=4(a-3)^2-6\{(a-2)^2+b^2+1\}\geqq0$
$4a^2-24a+36-6a^2+24a-24-6b^2-b\geqq0$
$-2a^2-6b^2+6\geqq0$
$a^2+3b^2-3\leqq0$
$\cfrac{a^2}{3}+b^2\leqq1$
$\cfrac{a^2}{(\sqrt{3})^2}+b^2\leqq1$

これは，楕円の方程式です。

したがって

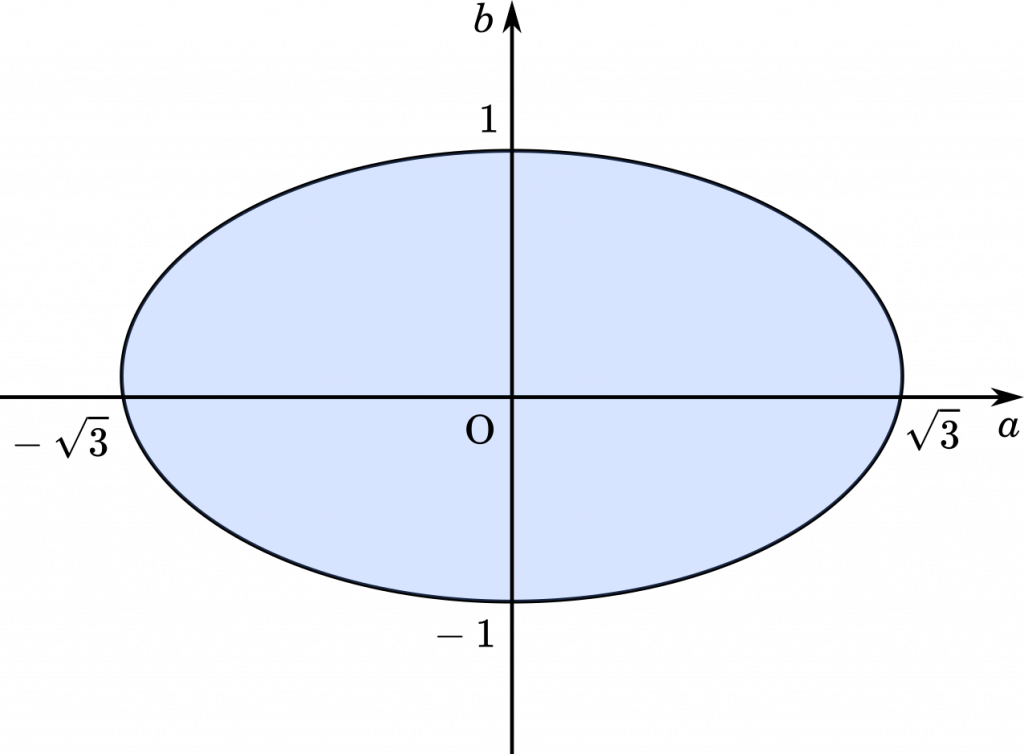
（答え）

球面と平面の共有点

(3)に進みます。

球面 $S$ の式は

$x^2+y^2+(z-1)^2=2$

でした。平面の式は $x=-1$ だから，これを代入すれば共有点が求められます。

$x=-1$ を代入して

$1+y^2+(z-1)^2=2$
$y^2+(z-1)^2=1$

これが直線 AP が共有点をもつので，共有点を Q とすると

$(bt)^2+(t-1-1)^2=1$
$b^2t^2+t^2-4t+4=1$
$(b^2+1)t^2-4t+3=0$ ・・・①

$x=-1$ より，$x=(a-2)t+2$ とすると

$(a-2)t+2=-1$
$(a-2)t=-3$
$t=-\cfrac{3}{a-2}$

①に代入して

$(b^2+1)\Big(-\cfrac{3}{a-2}\Big)^2-4\Big(-\cfrac{3}{a-2}\Big)+3=0$　$(a\not=2)$

$(b^2+1)\cfrac{9}{(a-2)^2}+\cfrac{12}{a-2}+3=0$

両辺に $(a-2)^2$ をかけて

$9(b^2+1)+12(a-2)+3(a-2)^2=0$
$3(b^2+1)+4(a-2)+(a-2)^2=0$
$3b^2+3+4a-8+a^2-4a+4=0$
$a^2+3b^2-1=0$
$a^2+3b^2=1$

これを楕円の方程式に持ち込みます。

$a^2+\cfrac{b^2}{\cfrac{1}{3}}=1$
$a^2+\cfrac{b^2}{\Big(\cfrac{1}{\sqrt{3}}\Big)^2}=1$

したがって

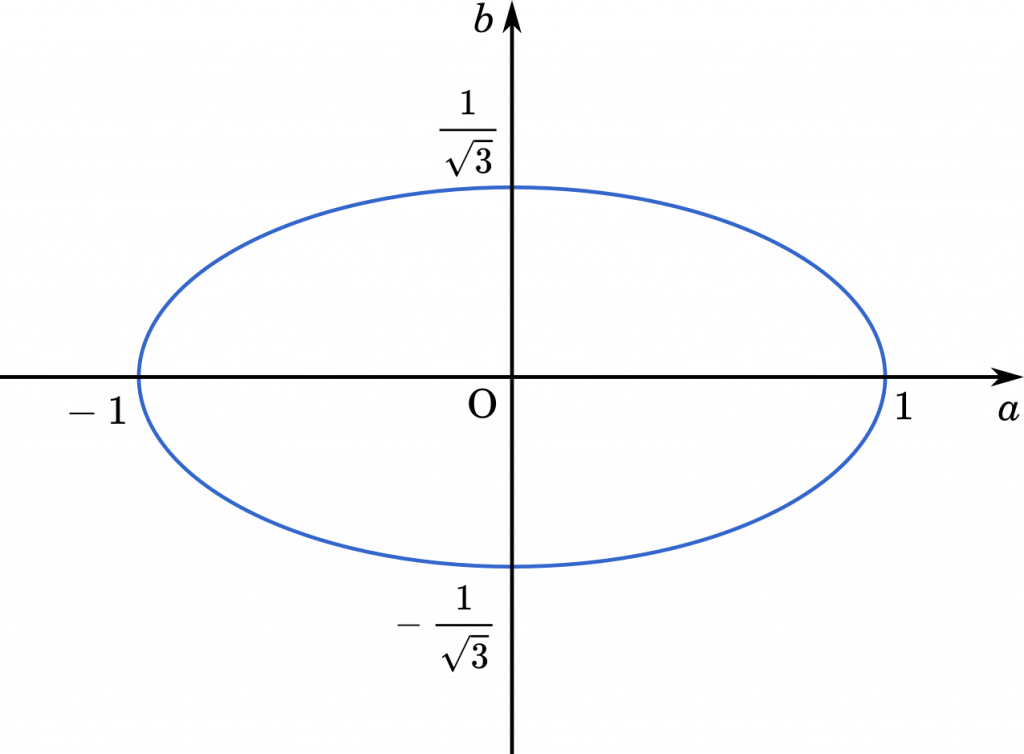
（答え）