【スマホで読む・わかりやすい】共通テスト試行H30年度数学IIB【解説・正解・問題】
第1問
〔1〕O を原点とする座標平面上に,点 A(0,-1) と,中心が O で半径が 1 の円 $C$ がある。円 $C$ 上に $y$ 座標が正である点 P をとり,線分 OP と $x$ 軸の正の部分とのなす角を $\theta(0$ < $\theta$ < $\pi)$ とする。また,円 $C$ 上に $x$ 座標が正である点 Q を,つねに ∠POQ=$\cfrac{\pi}{2}$ となるようにとる。次の問いに答えよ。
〔1〕(1)
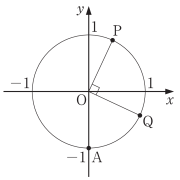
P,Q の座標をそれぞれ $\theta$ を用いて表すと
$\text{P}(\boxed{\text{ ア }},\boxed{\text{ イ }})$
$\text{Q}(\boxed{\text{ ウ }},\boxed{\text{ エ }})$
である。$\boxed{\text{ ア }}$~$\boxed{\text{ エ }}$ に当てはまるものを,次の⓪~⑤のうちから一つずつ選べ。ただし,ただし,同じものを繰り返し選んでもよい。
⓪ $\sin\theta$ ① $\cos\theta$
② $\tan\theta$ ③ $-\sin\theta$
④ $-\cos\theta$ ⑤ $-\tan\theta$
正解と解説
ア,イ 1, 0 ウ,エ 0, 4
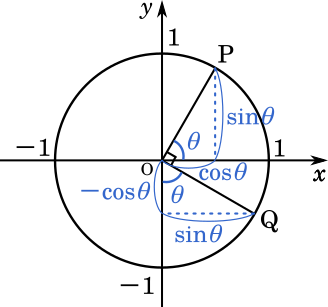
上の図より
$P(\cos\theta,\sin\theta)$
$Q(\sin\theta,-\cos\theta)$
〔1〕(2)
$\theta$ は 0 < $\theta$ < $\pi$ の範囲を動くものとする。このとき線分 AQ の長さ $\ell$ は $\theta$ の関数である。関数 $\ell$ のグラフとして最も適当なものを,次の ⓪ 〜 ⑨ のうちから一つ選べ。 $\boxed{\text{ オ }}$
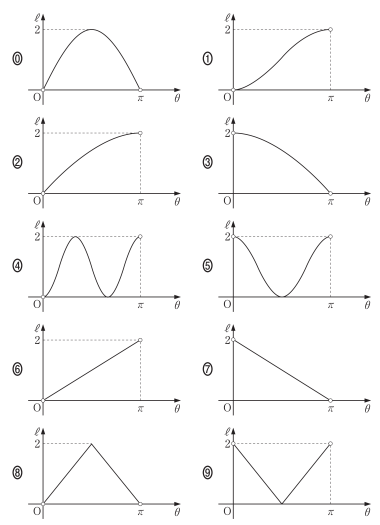
正解と解説
オ 2
余弦定理より
$\text{AQ}^2=\text{OA}^2+\text{OQ}^2-2\cdot\text{OA}\cdot\text{OQ}\cdot\cos\theta$
$\text{AQ}^2=2-2\cos\theta$
$\text{AQ}=\sqrt{2(1-\cos\theta)}$
$\theta=0$ のとき $AQ=\sqrt{2(1-1)}=0$
$\theta=\pi$ のとき $\text{AQ}=\sqrt{2\{1-(-1)\}}=2$
よって ①,②,④,⑥ のいずれかである。
また $\theta=\cfrac{\pi}{2}$ のとき $\text{AQ}=\sqrt{2(1-0)}=\sqrt{2}$
したがって,当てはまるのは ② である。
〔2〕 3次関数 $f(x)$ は,$x=-1$ で極小値 $-\cfrac{4}{3}$ をとり,$x=3$ で極大値をとる。また,曲線 $y=f(x)$ は点 (0,2) を通る。
〔2〕(1)
(1) $f(x)$ の導関数 $f'(x)$ は $\boxed{\text{ カ }}$ 次関数であり,$f'(x)$ は
$(x+\boxed{\text{ キ }})(x-\boxed{\text{ ク }})$
で割り切れる。
正解と解説
カ 2 キ,ク 1, 3
式を微分すると,微分した文字の次数は1つ下がる。3次式を微分すると2次式になる。また,問題文より $x=-1,3$ で $f'(x)$ が極値をとるということは,$x=-1,3$ は $f'(x)=0$ の解である。よって
$f'(x)=(x+1)(x-3)$
〔2〕(2)
$f(x)=\cfrac{\boxed{\text{ ケコ }}}{\boxed{\text{ サ }}}x^3+\boxed{\text{ シ }}x^2+\boxed{\text{ ス }}x+\boxed{\text{ セ }}$ である。
正解と解説
ケコ,サ,シ,ス,セ -2 3 2 6 2
$f(x)=ax^3+bx^2+cx+d$ とおくと
$f'(x)=3ax^2+2bx+c\cdots$①
(1)より式は $f'(x)=3a(x+1)(x-3)$ と書き換えることができる。式を展開して
$f'(x)=3a(x^2-2x-3)$
$=3ax^2-6ax-9a\cdots$②
①②を比べて
$2b=-6a$
$b=-3a\cdots$③
$c=-9a\cdots$④
また
$f(0)=d=2\cdots$⑤
③④⑤を $f(x)=ax^3+bx^2+cx+d$ に代入すると
$f(x)=ax^3-3ax^2-9ax+2\cdots$⑥
ここで $x=-1$ とすると
$f(-1)=-a-3a+9a+2=-\cfrac{4}{3}$
$a=-\cfrac{2}{3}$
③,④に代入して
$b=-3\Big(-\cfrac{2}{3}\Big)=2$
$c=-9\Big(-\cfrac{2}{3}\Big)=6$
したがって
$f(x)=-\cfrac{2}{3}x^3+2x^2+6x+2$
〔2〕(3)
方程式 $f(x)=0$ は,三つの実数解をもち,そのうち負の解は $\boxed{\text{ ソ }}$ 個である。
また,$f(x)=0$ の解を $a$,$b$,$c$ ( $a$ < $b$ < $c$) とし,曲線 $y=f(x)$ の$a$ ≦ $x$ ≦ $b$ の部分と $x$ 軸とで囲まれた図形の面積を $S$,曲線 $y=f(x)$ の $b$ ≦ $x$ ≦ $c$ の部分と $x$ 軸とで囲まれた図形の面積を $T$ とする。
このとき
$\displaystyle\int_a^c f(x)\space dx=\boxed{\text{ タ }}$
である。$\boxed{\text{ タ }}$ に当てはまるものを,次の⓪〜⑧のうちから一つ選べ。
⓪ $0$ ① $S$ ② $T$
③ $-S$ ④ $-T$ ⑤ $S+T$
⑥ $S-T$ ⑦ $-S+T$ ⑧ $-S-T$
正解と解説
ソ 2 タ 7
増減表を書くと
$\def\arraystretch{1.25}\begin{array}{c:c:c:c:c:c}x&\cdots&-1&\cdots&0&\cdots\\\hline f'(x)&-&0&+&+&+\\\hline f(x)&\searrow&-\frac{4}{3}&\nearrow&2&\nearrow\end{array}$
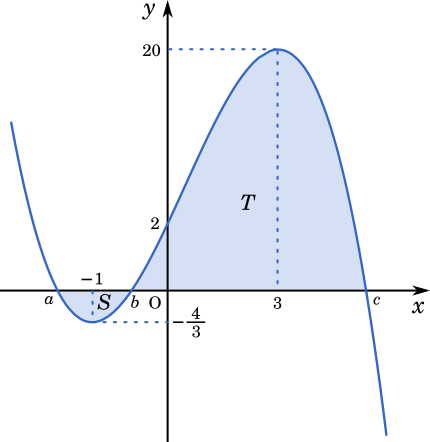
(2)より $f(x)=-\cfrac{2}{3}x^3+2x^2+6x+2$
上の図より $f(x)$ は $a,b$ で $x$ 軸の負の側と交わる。したがって,負の解は 2 個。
また $\displaystyle\int_a^c f(x)\space dx$ は図の色を塗った部分の面積を表す。
$\displaystyle\int_a^c f(x)\space dx=\int_a^b f(x)\space dx+\int_b^c f(x)\space dx$
ここで $\displaystyle\int_a^b f(x)\space dx$ は負の値となるので
$\displaystyle\int_a^c f(x)\space dx=-S+T$
〔3〕(1)
$\log_{10}2=0.3010$ とする。このとき,$10^{\space\boxed{\text{チ}}}=2$,$2^{\space\boxed{\text{ツ}}}=10$ となる。
$\boxed{\text{ チ }}$,$\boxed{\text{ ツ }}$ に当てはまるものを,次の ⓪ 〜 ⑧ のうちから一つずつ選べ。ただし,同じものを選んでもよい。
⓪ $0$ ① $0.3010$ ② $-0.3010$
③ $0.6990$ ④ $-0.6990$ ⑤ $\cfrac{1}{0.3010}$
⑥ $-\cfrac{1}{0.3010}$ ⑦ $\cfrac{1}{0.6990}$ ⑧ $-\cfrac{1}{0.6990}$
正解と解説
チ 1 ツ 5
$\log_{10} 2 = 0.3010\cdots$① より
$10^{0.3010}=2$
また,①の底を 2 に変換すると
$\cfrac{\log_2 2}{\log_2 10}=\cfrac{1}{\log_2 10}=0.3010$
$\log_2 10=\cfrac{1}{0.3010}$
(2)
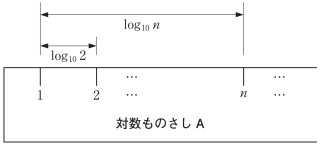
次のようにして対数ものさしAを作る。
対数ものさしA
2 以上の整数 $n$ のそれぞれに対して,1 の目盛りから右に $\log_{10} n$ だけ離れた場所に $n$ の目盛りを書く。
〔3〕(2)(i)
対数ものさしAにおいて,3 の目盛りと 4 の目盛りの間隔は,1 の目盛りと 2 の目盛りの間隔 $\boxed{\text{ テ }}$。$\boxed{\text{ テ }}$ に当てはまるものを,次の⓪〜②のうちから一つ選べ。
⓪ より大きい ① に等しい ② より小さい
正解と解説
テ 2
3 の目盛りと 4 の目盛りの間隔は
$\log_{10} 4-\log_{10} 3=\log_{10}\cfrac{4}{3}$
1 の目盛りと 2 の目盛りの間隔は
$\log_{10} 2-\log_{10} 1=\log_{10}\cfrac{2}{1}=\log_{10} 2$
真数を比べると $\cfrac{4}{3}$ < 2 より,3 の目盛りと 4 の目盛りの間隔は,1 の目盛りと 2 の目盛りの間隔より小さい。
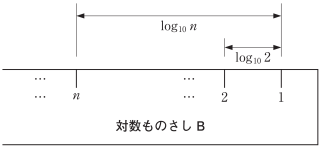
また,次のようにして対数ものさし B を作る。
対数ものさしB
2 以上の整数 $n$ のそれぞれに対して,1 の目盛りから左に $\log_{10} n$ だけ離れた場所に $n$ の目盛りを書く。
〔3〕(2)(ii)
次の図のように,対数ものさし A の 2 の目盛りと対数ものさし B の 1 の目盛りを合わせた。このとき,対数ものさし B の $b$ の目盛りに対応する対数ものさし A の目盛りは $a$ になった。
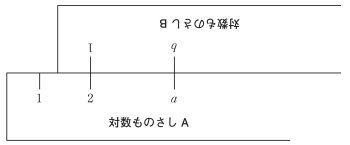
$a$ と $b$ の関係について,いつでも成り立つ式を,次の⓪〜③のうちから一つ選べ。 $\boxed{\text{ ト }}$
⓪ $a=b+2$ ① $a=2b$
② $a=\log_{10}(b+2)$ ③ $a=\log_{10}2b$
正解と解説
ト 1
ものさし A の 2 と $a$ の間隔と,ものさし B の 1 と $b$ の間隔が一致することを利用して恒等式を作ればよい。
$\log_{10} a-\log_{10} 2=\log_{10} b-\log_{10} 1$
$\log_{10} a-\log_{10} b=\log_{10} 2-\log_{10} 1$
$\log_{10}\cfrac{a}{b}=\log_{10} 2-0$
$\cfrac{a}{b}=2$
$a=2b$
さらに,次のようにしてものさし C を作る。
ものさし C
自然数 $n$ のそれぞれに対して,0 の目盛りから左に $n\log_{10} 2$ だけ離れた場所に $n$ の目盛りを書く。
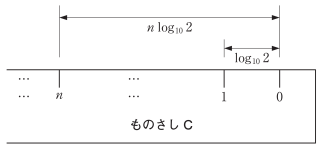
〔3〕(2)(iii)
次の図のように対数ものさし A の 1 の目盛りとものさし C の 0 の目盛りを合わせた。このとき,ものさし C の $c$ の目盛りに対応する対数ものさし A の目盛りは $d$ になった。
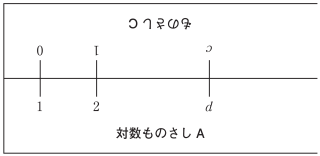
$c$ と $d$ の関係について,いつでも成り立つ式を,次の⓪〜③のうちから一つ選べ。 $\boxed{\text{ ナ }}$
⓪ $d=2c$ ① $d=c^2$
② $d=2^c$ ③ $c=\log_{10}d$
正解と解説
ナ 2
ものさしAの 1 と $d$ の間隔と,ものさし C の 0 と $c$ の間隔が一致することを利用して恒等式を作ればよい。
$\log_{10}d-\log_{10}1=c\log_{10}2$
$\log_{10}d-0=\log_{10}2^c$
$d=2^c$
〔3〕(2)(iv)
対数ものさし A と対数ものさし B の目盛りを一度だけ合わせるか,対数ものさし A とものさし C の目盛りを一度だけ合わせることにする。
このとき,適切な箇所の目盛りを読み取るだけで実行できるものを,次の⓪〜⑤のうちからすべて選べ。$\boxed{\text{ ニ }}$
⓪ 17 に 9 を足すこと。
① 23 から 15 を引くこと。
② 13 に 4 をかけること。
③ 63 を 9 で割ること。
④ 2 を 4 乗すること。
⑤ $\log_{2}64$ の値を求めること。
正解と解説
ニ 2, 3, 4, 5
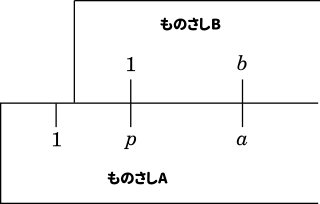
ものさし A とものさし B を上の図のように置き,ものさし A の $p$ と $a$ の間隔と,ものさし B の 1 と $b$ の間隔を一致させる。
$\log_{10}a-\log_{10}p=\log_{10}b-\log_{10}1$
$\cfrac{a}{p}=b\cdots$①
$a=pb\cdots$②
①を利用すれば $a$ を $p$ で割ることができる。
②を利用すれば $b$ に $p$ をかけることができる。
つまり,整数のかけ算と割り算が行える。
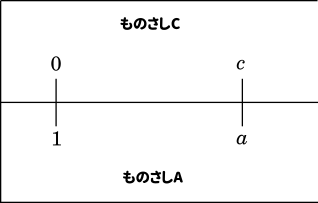
次に,ものさし A とものさし C を上の図のように置き,ものさし A の 1 と $a$ の間隔と,ものさしCの 0 と $c$ の間隔を一致させる。
$\log_{10}a-\log_{10}1=c\log_{10}2$
$\log_{10}a=\log_{10}2^c$
$a=2^c\cdots$③
③に $c=4$ を代入することで,2 を 4 乗することができる。
また,$a=64$ とおくと
$64=2^c$
$\log_{2}64=c$
したがって,ものさしAの 64 に一致するものさし C の値が $\log_{2}64$ の値となる。
SNSでシェア