【スマホで読む・わかりやすい】共通テスト試行H30年度数学IIB【解説・正解・問題】
第5問
(1)
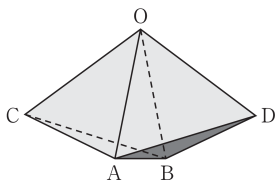
右の図のような立体を考える。ただし,六つの面 OAC,OBC,OAD,OBD,ABC,ABD は 1 辺の長さが 1 の正三角形である。この立体の∠COD の大きさを調べたい。
線分 AB の中点を M,線分 CD の中点を N とおく。
$\overrightarrow{\text{OA}}=\vec{a}$,$\overrightarrow{\text{OB}}=\vec{b}$,$\overrightarrow{\text{OC}}=\vec{c}$,$\overrightarrow{\text{OD}}=\vec{d}$ とおくとき,次の問いに答えよ。
(1)(i)
次の $\boxed{\text{ ア }}$ 〜 $\boxed{\text{ エ }}$ に当てはまる数を求めよ。
$\overrightarrow{\text{OM}}=\cfrac{\boxed{\text{ ア }}}{\boxed{\text{ イ }}}(\vec{a}+\vec{b})$,$\overrightarrow{\text{ON}}=\cfrac{\boxed{\text{ ア }}}{\boxed{\text{ イ }}}(\vec{c}+\vec{d})$
$\displaystyle\vec{a}\cdot\vec{b}=\vec{a}\cdot\vec{c}=\vec{a}\cdot\vec{d}=\vec{b}\cdot\vec{c}=\vec{b}\cdot\vec{d}=\cfrac{\boxed{\text{ ウ }}}{\boxed{\text{ エ }}}$
正解と解説
ア,イ,ウ,エ 1, 2, 1, 2
中点を求めると
$\overrightarrow{\text{OM}}=\cfrac{1}{2}(\vec{a}+\vec{b})$
同様にして
$\overrightarrow{\text{ON}}=\cfrac{1}{2}(\vec{c}+\vec{d})$
OAB は 1 辺の長さが 1 の正三角形より,∠AOB=60° だから
$\vec{a}\cdot\vec{b}=|\vec{a}||\vec{b}|\cos$ 60°
$=1\cdot1\cdot\cfrac{1}{2}=\cfrac{1}{2}$
その他も同様に正三角形を用いて
$\displaystyle\vec{a}\cdot\vec{b}=\vec{a}\cdot\vec{c}=\vec{a}\cdot\vec{d}=\vec{b}\cdot\vec{c}=\vec{b}\cdot\vec{d}=\cfrac{1}{2}$
(1)(ii)
3 点 O,N,M は同一直線上にある。内積 $\overrightarrow{\text{OA}}\cdot\overrightarrow{\text{CN}}$ の値を用いて,$\overrightarrow{\text{ON}}=k\overrightarrow{\text{OM}}$ を満たす $k$ の値を求めよ。
$k=\cfrac{\boxed{\text{ オ }}}{\boxed{\text{ カ }}}$
正解と解説
解答・解説
オ,カ 2, 3
ベクトルを $\vec{a}$,$\vec{b}$,$\vec{c}$,$\vec{d}$ で表すことを考える
$\overrightarrow{\text{CN}}=\overrightarrow{\text{ON}}-\overrightarrow{\text{OC}}$ より
$\overrightarrow{\text{OA}}\cdot\overrightarrow{\text{CN}}=\overrightarrow{\text{OA}}(\overrightarrow{\text{ON}}-\overrightarrow{\text{OC}})$
$=\overrightarrow{\text{OA}}\cdot\overrightarrow{\text{ON}}-\overrightarrow{\text{OA}}\cdot\overrightarrow{\text{OC}}$
$=\vec{a}\cdot\cfrac{1}{2}(\vec{c}+\vec{d})-\vec{a}\cdot\vec{c}$
$=\cfrac{1}{2}(\vec{a}\cdot\vec{c}+\vec{a}\cdot\vec{d})-\vec{a}\cdot\vec{c}$
$=\cfrac{1}{2}\Big(\cfrac{1}{2}+\cfrac{1}{2}\Big)-\cfrac{1}{2}$
$=0$
$\overrightarrow{\text{OA}}\cdot\overrightarrow{\text{CN}}=0$ より
$\overrightarrow{\text{OA}}\cdot\overrightarrow{\text{ON}}-\overrightarrow{\text{OA}}\cdot\overrightarrow{\text{OC}}=0$
ここで $\overrightarrow{\text{ON}}=k\overrightarrow{\text{OM}}$ として
$k\overrightarrow{\text{OA}}\cdot\overrightarrow{\text{OM}}-\overrightarrow{\text{OA}}\cdot\overrightarrow{\text{OC}}=0$
$k\vec{a}\cdot\cfrac{1}{2}(\vec{a}+\vec{b})-\vec{a}\cdot\vec{c}=0$
$\cfrac{1}{2}k|\vec{a}|^2+\cfrac{1}{2}k\vec{a}\cdot\vec{b}-\vec{a}\cdot\vec{c}=0$
$|\vec{a}|^2=1$ だから
$\cfrac{1}{2}k+\cfrac{1}{2}k\cdot\cfrac{1}{2}-\cfrac{1}{2}=0$
$k=\cfrac{2}{3}$
(1)(iii)
∠COD = $\theta$ とおき,$\cos\theta$ の値を求めたい。次の方針 1 または方針 2 について,$\boxed{\text{ キ }}$ 〜 $\boxed{\text{ シ }}$ に当てはまる数を求めよ。
方針 1
$\vec{d}$ を $\vec{a}$,$\vec{b}$,$\vec{c}$ を用いて表すと,
$\vec{d}=\cfrac{\boxed{\text{ キ }}}{\boxed{\text{ ク }}}\vec{a}+\cfrac{\boxed{\text{ ケ }}}{\boxed{\text{ コ }}}\vec{b}-\vec{c}$
であり,$\vec{c}\cdot\vec{d}=\cos\theta$ から $\cos\theta$ が求められる。
方針 2
$\overrightarrow{\text{OM}}$ と $\overrightarrow{\text{ON}}$ のなす角を考えると,$\overrightarrow{\text{OM}}\cdot\overrightarrow{\text{ON}}=|\overrightarrow{\text{OM}}||\overrightarrow{\text{ON}}|$ が成り立つ。
$|\overrightarrow{\text{ON}}|^2=\cfrac{\boxed{\text{ サ }}}{\boxed{\text{ シ }}}+\cfrac{1}{2}\cos\theta$ であるから,$\overrightarrow{\text{OM}}\cdot\overrightarrow{\text{ON}}$,$|\overrightarrow{\text{OM}}|$ の値を用いると,$\cos\theta$ が求められる。
正解と解説
キ,ク,ケ,コ,サ,シ 2, 3, 2, 3, 1, 2
$\overrightarrow{\text{ON}}=\cfrac{2}{3}\overrightarrow{\text{OM}}$ より
$\cfrac{1}{2}(\vec{c}+\vec{d})=\cfrac{2}{3}\cdot\cfrac{1}{2}(\vec{a}+\vec{b})$
$\vec{c}+\vec{d}=\cfrac{2}{3}\vec{a}+\cfrac{2}{3}\vec{b}$
$\vec{d}=\cfrac{2}{3}\vec{a}+\cfrac{2}{3}\vec{b}-\vec{c}$
また
$\overrightarrow{\text{ON}}=\cfrac{1}{2}(\vec{c}+\vec{d})$ より
$|\overrightarrow{\text{ON}}|^2=\Big\{\cfrac{1}{2}(\vec{c}+\vec{d})\Big\}^2$
$=\cfrac{1}{4}(\vec{c}+\vec{d})^2$
$=\cfrac{1}{4}(|\vec{c}|^2+2\vec{c}\cdot\vec{d}+|\vec{d}|^2)$
$=\cfrac{1}{4}(1+2\vec{c}\cdot\vec{d}+1)$
$=\cfrac{1}{2}+\cfrac{1}{2}\vec{c}\cdot\vec{d}$
$=\cfrac{1}{2}+\cfrac{1}{2}|\vec{c}||\vec{d}|\cos\theta$
ここで $|\vec{c}|=1$,$|\vec{d}|=1$ だから
$=\cfrac{1}{2}+\cfrac{1}{2}\cos\theta$
(1)(iv)
方針 1 または方針 2 を用いて $\cos\theta$ の値を求めよ。
$\cos\theta=\cfrac{\boxed{\text{ スセ }}}{\boxed{\text{ ソ }}}$
正解と解説
スセ,ソ -1, 3
$\overrightarrow{\text{OM}}\cdot\overrightarrow{\text{ON}}=\cfrac{1}{2}(\vec{a}+\vec{b})\cdot\cfrac{1}{2}(\vec{c}+\vec{d})$
$=\cfrac{1}{4}(\vec{a}\cdot\vec{c}+\vec{a}\cdot\vec{d}+\vec{b}\cdot\vec{c}+\vec{b}\cdot\vec{d})$
$=\cfrac{1}{4}\Big(\cfrac{1}{2}+\cfrac{1}{2}+\cfrac{1}{2}+\cfrac{1}{2}\Big)=\cfrac{1}{2}$
ここで,$\overrightarrow{\text{ON}}=\cfrac{2}{3}\overrightarrow{\text{OM}}$ より ON と OM は一直線上にあるので
$\overrightarrow{\text{OM}}\cdot\overrightarrow{\text{ON}}=|\overrightarrow{\text{OM}}||\overrightarrow{\text{ON}}|\cos 0\degree$
$|\overrightarrow{\text{OM}}||\overrightarrow{\text{ON}}|=\cfrac{1}{2}$
ここから
$|\overrightarrow{\text{ON}}|=\cfrac{1}{2|\overrightarrow{\text{OM}}|}$ より,両辺を2乗して
$|\overrightarrow{\text{ON}}|^2=\cfrac{1}{4|\overrightarrow{\text{OM}}|^2}$
また $\overrightarrow{\text{OM}}=\cfrac{1}{2}(\vec{a}+\vec{b})$ より
$|\overrightarrow{\text{OM}}|^2=\cfrac{1}{4}(\vec{a}+\vec{b})^2$
$=\cfrac{1}{4}(|\vec{a}|^2+2\vec{a}\cdot\vec{b}+|\vec{b}|^2)$
$=\cfrac{1}{4}(1+2\cdot\cfrac{1}{2}+1)=\cfrac{3}{4}$
したがって
$|\overrightarrow{\text{ON}}|^2=\cfrac{1}{4\cdot\cfrac{3}{4}}=\cfrac{1}{3}$
方針2の式に代入して
$\cfrac{1}{3}=\cfrac{1}{2}+\cfrac{1}{2}\cos\theta$
$\cos\theta=-\cfrac{1}{3}$
(2)
(1)の図形から,四つの面 OAC,OBC,OAD,OBD だけを使って,下のような図形を作成したところ,この図形は ∠AOB を変化させると,それにともなって ∠COD も変化することがわかった。
∠AOB= $\alpha$,∠COD= $\beta$ とおき,$\alpha$ > 0,$\beta$ > 0 とする。このときも,線分 AB の中点と線分 CD の中点および点 O は一直線上にある。
(2)(i)
$\alpha$ と $\beta$ が満たす関係式は(1)の方針 2 を用いると求めることができる。その関係式として正しいものを,次の ⓪ 〜 ④ のうちから一つ選べ。 $\boxed{\text{ タ }}$
⓪ $\cos\alpha+\cos\beta=1$
① $(1+\cos\alpha)(1+\cos\beta)=1$
② $(1+\cos\alpha)(1+\cos\beta)=-1$
③ $(1+2\cos\alpha)(1+2\cos\beta)=\cfrac{2}{3}$
④ $(1-\cos\alpha)(1-\cos\beta)=\cfrac{2}{3}$
正解と解説
タ 1
(1)で求めた $|\overrightarrow{\text{OM}}||\overrightarrow{\text{ON}}|=\cfrac{1}{2}$ はここでも同じ計算をすることになるので,そのまま用いることができる。
また
$\vec{a}\cdot\vec{b}=|\vec{a}||\vec{b}|\cos\alpha=\cos\alpha$
$\vec{c}\cdot\vec{d}=|\vec{c}||\vec{d}|\cos\beta=\cos\beta$
となり,(1)で求めた式に代入することができる。
$|\overrightarrow{\text{OM}}|^2=\cfrac{1}{2}+\cfrac{1}{2}\vec{a}\cdot\vec{b}=\cfrac{1}{2}+\cfrac{1}{2}\cos\alpha$
$|\overrightarrow{\text{ON}}|^2=\cfrac{1}{2}+\cfrac{1}{2}\vec{c}\cdot\vec{d}=\cfrac{1}{2}+\cfrac{1}{2}\cos\beta$
$|\overrightarrow{\text{OM}}||\overrightarrow{\text{ON}}|=\cfrac{1}{2}$ より,両辺を2乗して
$|\overrightarrow{\text{OM}}|^2|\overrightarrow{\text{ON}}|^2=\cfrac{1}{4}$
$(\cfrac{1}{2}+\cfrac{1}{2}\cos\alpha)(\cfrac{1}{2}+\cfrac{1}{2}\cos\beta)=\cfrac{1}{4}$
$(1+\cos\alpha)(1+\cos\beta)=1$
(2)(ii)
$\alpha$ = $\beta$ のとき,$\alpha$ =$\boxed{\text{ チツ }}$° であり,このとき,点 D は $\boxed{\text{ テ }}$ にある。$\boxed{\text{ チツ }}$ に当てはまる数を求めよ。また,$\boxed{\text{ テ }}$ に当てはまるものを,次の⓪〜②のうちから一つ選べ。
⓪ 平面 ABC に関して O と同じ側
① 平面 ABC 上
② 平面 ABC に関して O と異なる側
正解と解説
チツ 90 テ 1
$\alpha$ = $\beta$ より
$(1+\cos\alpha)(1+\cos\alpha)=1$
$1+2\cos\alpha+\cos^2\alpha=1$
$2\cos\alpha+\cos^2\alpha=0$
$\cos\alpha(2+\cos\alpha)=0$
$\cos\alpha=0,-2$
-1 ≦ $\cos\alpha$ ≦ 1 より
$\cos\alpha$ =0
$\alpha$=90°
また $\alpha$ = $\beta$ =90° とおくと
$|\overrightarrow{\text{OM}}|^2=\cfrac{1}{2}+\cfrac{1}{2}\cos 90\degree=\cfrac{1}{2}$
$|\overrightarrow{\text{ON}}|^2=\cfrac{1}{2}+\cfrac{1}{2}\cos 90\degree=\cfrac{1}{2}$
つまり,点 M と 点 N は同じ位置にある。
また,点 M は AB の中点だから平面 ABC 上にある。また点 D は CM の延長線上にあるので平面 ABC 上にある。
SNSでシェア