【スマホで読む・わかりやすい】共通テスト試行H30年度数学IIB【解説・正解・問題】
第2問
〔1〕 100 g ずつ袋詰めされている食品 A と B がある。 1 袋あたりのエネルギーは食品 A が 200 kcal,食品 B が 300 kcal であり, 1 袋あたりの脂質の含有量は食品 A が 4 g,食品 B が 2 g である。
(1) 太郎さんは,食品 A と B を食べるにあたり,エネルギーは 1500 kcal以下に,脂質は 16 g 以下に抑えたいと考えている。食べる量(g)の合計が最も多くなるのは,食品 A と B をどのような量の組合せで食べるときかを調べよう。ただし,一方のみを食べる場合も含めて考えるものとする。
〔1〕(1)(i)
食品 A を $x$ 袋分,食品 B を $y$ 袋分だけ食べるとする。
このとき,$x,y$ は次の条件①,②を満たす必要がある。
摂取するエネルギー量についての条件 $\boxed{\text{ ア }}\cdots\cdots$①
摂取する脂質の量についての条件 $\boxed{\text{ イ }}\cdots\cdots$②
$\boxed{\text{ ア }}$ ,$\boxed{\text{ イ }}$ に当てはまる式を,次の各解答群のうちから一つずつ選べ。
$\boxed{\text{ ア }}$ の解答群
⓪ $200x + 300y \leqq 1500$
① $200x + 300y \geqq 1500$
② $300x + 200y \leqq 1500$
③ $300x + 200y \geqq 1500$
$\boxed{\text{ イ }}$ の解答群
⓪ $2x + 4y \leqq 16$
① $2x + 4y \geqq 16$
② $4x + 2y \leqq 16$
③ $4x + 2y \geqq 16$
正解
解答
ア,イ 0, 2
〔1〕(1)(ii)
$x$,$y$ の値と条件①,②の関係について正しいものを,次の⓪〜③のうちから二つ選べ。ただし,解答の順序は問わない。$\boxed{\text{ ウ }}$,$\boxed{\text{ エ }}$
⓪ $(x,y)=(0,5)$は条件①を満たさないが,条件②は満たす。
① $(x,y)=(5,0)$は条件①を満たすが,条件②は満たさない。
② $(x,y)=(4,1)$は条件①も条件②も満たさない。
③ $(x,y)=(3,2)$は条件①と条件②をともに満たす。
正解と解説
ウ,エ 1, 3
⓪ $(x,y)=(0,5)$ のとき
$200\times0+300\times5=1500\cdots$①を満たす
$4\times0+2\times5=10\cdots$②を満たす
① $(x,y)=(5,0)$ のとき
$200\times5+300\times0=1000\cdots$①を満たす
$4\times5+2\times0=20\cdots$②を満たさない
② $(x,y)=(4,1)$ のとき
$200\times4+300\times1=1100\cdots$①を満たす
$4\times4+2\times1=18\cdots$②を満たさない
③ $(x,y)=(3,2)$ のとき
$200\times3+300\times2=1200\cdots$①を満たす
$4\times3+2\times2=16\cdots$②を満たす
〔1〕(1)(iii)
条件①,②をともに満たす$(x,y)$について,食品 A と B を食べる量の合計の最大値を二つの場合で考えてみよう。
食品 A,B が 1 袋を小分けにして食べられるような食品のとき,すなわち $x$,$y$ のとり得る値が実数の場合,食べる量の合計の最大値は $\boxed{\text{ オカキ }}$ g である。このときの $(x,y)$ の組は,
$(x,y)=\Big(\cfrac{\boxed{\text{ ク }}}{\boxed{\text{ ケ }}},\cfrac{\boxed{\text{ コ }}}{\boxed{\text{ サ }}}\Big)$ である。
次に,食品 A,B が 1 袋を小分けにして食べられないような食品のとき,すなわち $x$,$y$ のとり得る値が整数の場合,食べる量の合計の最大値は $\boxed{\text{ シスセ}}$ g である。このときの $(x,y)$ の組は $\boxed{\text{ ソ }}$ 通りある。
正解と解説
オカキ 575 ク ケ, コ サ 9 4, 7 2
シスセ 500 ソ 4
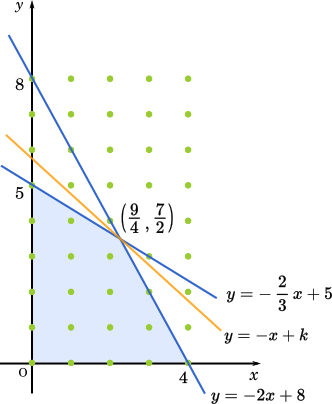
条件①,②をともに満たす$(x,y)$ の領域を取ると,上の図の青色で塗りつぶした部分になる。
$200x+300y=1500$ とおくと
$y=-\cfrac{2}{3}x+5\cdots$①’
また,$4x+2y=16$ とおくと
$y=-2x+8\cdots$②’
ここで,食べる量の合計を $k$ とおくと
$x+y=k$
$y=-x+k$
$y=-x+k$ のグラフは $k$ の値によって縦方向に平行移動する。このとき,直線と青色の領域が重なる範囲における $k$ の最大値を考えると,直線が①’と②’の交点を通る場合である。
連立して①’と②’の交点を求めると
①’×3 $\cdots 2x+3y=15$
②’ $\cdots 2x+y=8$
$2y=7$
$y=\cfrac{7}{2}$
②’に代入して $x=\cfrac{9}{4}$
$k$ を求めると
$100\times\cfrac{9}{4}+100\times\cfrac{7}{2}=575$
次に,$x$,$y$ がともに整数である場合を考える。
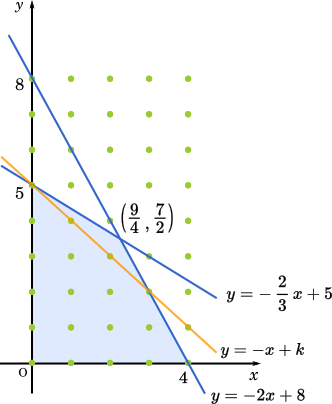
$x$,$y$ がともに整数である場合,$y=-x+k$ は格子点上を通過する。この条件で考えると,$k=5$ のときに $x+y$ は最大となる。このとき,$(x,y)$ は (0,5),(1,4),(2,3),(3,2) の 4 通り。
〔1〕(2)
花子さんは,食品 A と B を合計 600 g 以上食べて,エネルギーは 1500 kcal以下にしたい。脂質を最も少なくできるのは,食品 A,B が 1 袋を小分けにして食べられない食品の場合,A を $\boxed{\text{ タ }}$ 袋,B を $\boxed{\text{ チ }}$ 袋食べるときで,そのときの脂質は $\boxed{\text{ ツテ }}$ g である。
正解と解説
タ 3 チ 3 ツテ 18
一袋が 100g であることに注意して,問題文の条件を式として表すと
$100x+100y$ ≧ $600\cdots$③
$200x+300y$ ≦ $1500\cdots$④
③を変形して $y$ ≧ $-x+6\cdots$③’
④を変形して $y$ ≦ $-\cfrac{2}{3}x+5\cdots$④’
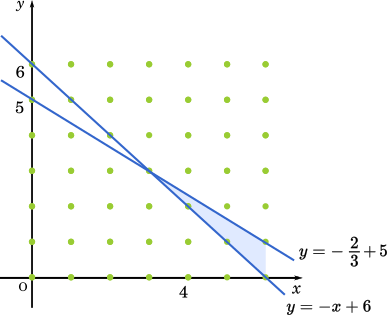
③’,④’を同時に満たす領域を示すと上の図の青色の部分となる。食べる袋の数がマイナスになることはないので,$x$ ≧ 0,y ≧ 0 であることにも注意する。
$x$,$y$ は整数だから,青色の領域上にある格子点が条件に当てはまる。よって
($x,y$)=(3,3),(4,2),(5,1),(6,0),(6,1)
脂質の量は $4x+2y$ だから,脂質が最も少なくなる組み合わせは (3,3) である。
$4\times3+2\times3=18$(g)
〔2〕
(1) 座標平面上に点 A をとる。点 P が放物線 $y=x^2$ 上を動くとき,線分 AP の中点 M の軌跡を考える。
〔2〕(1)(i)
点 A の座標が (0,-2) のとき,点 M の軌跡の方程式として正しいものを,次の⓪〜⑤のうちから一つ選べ。 $\boxed{\text{ ト }}$
⓪ $y=x^2-1$ ① $y=2x^2-1$
② $y=\cfrac{1}{2}x^2-1$ ③ $y=|x|-1$
④ $y=2|x|-1$ ⑤ $y=\cfrac{1}{2}|x|-1$
正解と解説
ト 1
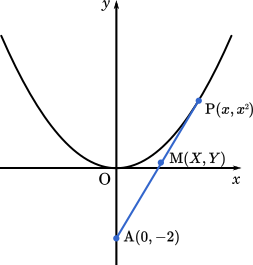
点 M $(X,Y)$ とおくと
$X=\cfrac{x+0}{2}=\cfrac{x}{2}\cdots$①
$Y=\cfrac{x^2-2}{2}\cdots$②
①より $x=2X$
②に代入して
$Y=\cfrac{(2X)^2-2}{2}=2X^2-1$
〔2〕(1)(ii)
$p$ を実数とする。点 A の座標が ($p$,-2) のとき,点 M の軌跡は(i)の軌跡を $x$ 軸方向に $\boxed{\text{ ナ }}$ だけ平行移動したものである。$\boxed{\text{ ナ }}$ に当てはまるものを,次の⓪〜⑤のうちから一つ選べ。
⓪ $\cfrac{1}{2}p$ ① $p$ ② $2p$
③ $-\cfrac{1}{2}p$ ④ $-p$ ⑤ $-2p$
正解と解説
ナ 0
点A ($p$,-2) として,点 M $(X,Y)$ を求めると
$X=\cfrac{x+p}{2}\cdots$③
$Y=\cfrac{X-2}{2}\cdots$④
③を変形して
$2X=x+p$
$x=2X-p$
④に代入して
$Y=\cfrac{(2X-p)^2-2}{2}$
$=\cfrac{4X^2-4pX+p^2-2}{2}$
$=2X^2-2pX+\cfrac{p^2}{2}-1$
平方完成すると
$=2(X-pX)+\cfrac{p^2}{2}-1$
$=2\Big(X-\cfrac{p}{2}\Big)^2-\cfrac{p^2}{2}+\cfrac{p^2}{2}^1$
$=2\Big(X-\cfrac{p}{2}\Big)^2-1$
〔2〕(1)(iii)
$p$,$q$ を実数とする。点 A の座標が $(p,q)$ のとき,点 M の軌跡と放物線 $y=x^2$ との共有点について正しいものを,次の⓪〜⑤のうちからすべて選べ。 $\boxed{\text{ ニ }}$
⓪ $q=0$ のとき,共有点はつねに 2 個である。
① $q=0$ のとき,共有点が 1 個になるのは $p=0$ のときだけである。
② $q=0$ のとき,共有点は 0 個, 1 個, 2 個のいずれの場合もある。
③ $q$ < $p^2$ のとき,共有点はつねに 0 個である。
④ $q=p^2$ のとき,共有点はつねに 1 個である。
⑤ $q$ > $p^2$ のとき,共有点はつねに 0 個である。
正解と解説
ニ 1, 4, 5
(i),(ii)と同様に点 M $(X,Y)$ を求める
$X=\cfrac{x+p}{2}$ より
$x=2X-p$
$Y=\cfrac{x^2+q}{2}$
$=\cfrac{(2X-p)^2+q}{2}$
$=2X^2-2pX+\cfrac{p^2+q}{2}$
判別式を求めると
$\cfrac{D}{4}=p^2-\cfrac{p^2+q}{2}=\cfrac{p^2-q}{2}$
$q=0$ をおくと
$p=0$ のとき $D=0$ だから,共有点は1個
$p$ ≠ 0 のとき $D$ > 0 だから,共有点は 2 個
また
$q$ < $p^2$ のとき $D$ > 0 だから,共有点は 2 個
$q=p^2$ のとき $D=0$ だから,共有点は 1 個
$q$ > $p^2$ のとき $D$ < $0$ だから,共有点は 0 個
以上の条件に当てはまるのは選択肢①,④,⑤である。
〔1〕(2)
ある円 $C$ 上を動く点 Q がある。下の図は定点 O (0,0),$\text{A}_1$(-9,0),$\text{A}_2$(-5,-5),$\text{A}_3$(5,-5),$\text{A}_4$(9,0) に対して,線分 OQ,$\text{A}_1\text{Q}$,$\text{A}_2\text{Q}$,$\text{A}_3\text{Q}$,$\text{A}_4\text{Q}$ のそれぞれの中点の軌跡である。このとき,円 $C$ の方程式として最も適当なものを,下の⓪〜⑦のうちから一つ選べ。 $\boxed{\text{ ヌ }}$
⓪ $x^2+y^2=1$ ① $x^2+y^2=2$
② $x^2+y^2=4$ ③ $x^2+y^2=16$
④ $x^2+(y+1)^2=1$ ⑤ $x^2+(y+1)^2=2$
⑥ $x^2+(y+1)^2=4$ ⑦ $x^2+(y+1)^2=16$
正解と解説
ヌ 3
この設問では,それぞれ中点の軌跡の中心座標や半径ははっきりと示されていない。ただし,原点を中心とする半径 2 の円だけは分かっているので,これについて仮説を立て,選択肢を絞り込んでいく。問題文で「最も正しいもの」と尋ねられているのはそのためである。
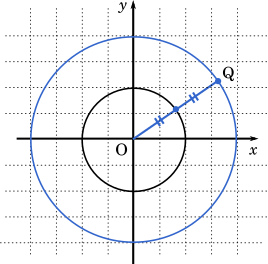
ここで,原点を中心とする半径 4 の円を描くと,円上の点と原点との中点の軌跡が原点を中心する半径 2 の円になることが分かる。よって,円 $C$ を $x^2+y^2=4^2$ と仮定する。
もし,円 $C$ の中心が原点ではない場合,例えば選択肢の $x^2+(y+1)^2=16$ であると仮定してみよう。
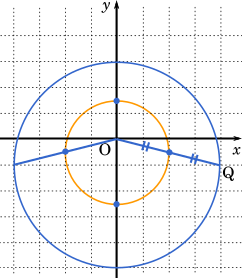
数か所で点 Q と原点の中点を取ってみると,上の図のオレンジ色のような円を描くことができる。このとき,この円の中心は原点ではない。このように,円 $C$ の中心が原点ではない場合,原点を中心する軌跡を描くことはできない。点 Q と$\text{A}_1$~$\text{A}_4$についても同様であることは容易に確かめられるだろう。
こうして,選択肢④~⑦は除かれる。また,選択⓪~③は原点を中心する円であるが,点 Q と原点の中点の軌跡が半径 2 の円になるのは $x^2+y^2=16$ のみである。よって③が最も適当である。
SNSでシェア