【スマホで読む・わかりやすい】共通テスト試行H30年度数学IA【解説・正解・問題】
第5問
ある日,太郎さんと花子さんのクラスでは,数学の授業で先生から次の問題1が宿題として出された。下の問いに答えよ。なお,円周上に異なる 2 点をとった場合,弧は二つできるが,本問題において,弧は二つあるうちの小さい方を指す。
問題1 正三角形 ABC の外接円の弧 BC 上に点 X があるとき,AX = BX + CX が成り立つことを証明せよ。
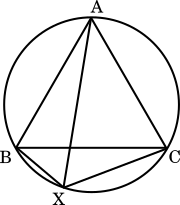
(1)
問題1は次のような構想をもとにして証明できる。
線分 AX 上に BX = B’X となる点B’ をとり,B と B’ を結ぶ。
AX = AB’ + B’X なので,AX = BX + CX を示すには,AB’ = CX を示せばよく,AB = CX を示すには,二つの三角形 $\boxed{\text{ ア }}$ と $\boxed{\text{ イ }}$ が合同であることを示せばよい。
$\boxed{\text{ ア }}$,$\boxed{\text{ イ }}$ に当てはまるものを,次の⓪~⑦のうちから一つずつ選べ。ただし,$\boxed{\text{ ア }}$,$\boxed{\text{ イ }}$ の解答の順序は問わない。
⓪ △ABB’ ① △AB’C ② △ABX ③ △AXC
④ △BCB’ ⑤ △BXB’ ⑥ △B’XC ⑦ △CBX
正解と解説
ア,イ 0,7
△ABB’ と △CBX において
△ABC は正三角形より BA=BC$\cdots$①
円周角の定理より
∠BAX=BCX$\cdots$②
また
∠ACB=∠AXB=60°$\cdots$③
△BXB’ は二等辺三角形であり底角が等しいので
∠XBB’=∠XB’B=60°
よって,△BXB’ は正三角形である。
さらに
∠XBC=∠XBB’-∠CBB’=60°-∠CBB’
∠B’BA=∠CBA-∠CBB’=60°-∠CBB’
よって
∠XBC=∠B’BA$\cdots$④
①,②,④より1辺とその両端の角がそれぞれ等しいので
△ABB’≡△CBX
太郎さんたちは,次の日の数学の授業で問題1を証明した後,点 X が弧 BC 上にないときについて先生に質問をした。その質問に対して先生は,一般に次の定理が成り立つことや,その定理と問題1で証明したことを使うと,下の問題2が解決できることを教えてくれた。
定理 平面上の点 X と正三角形 ABC の各頂点からの距離 AX,BX,CX について,点 X が三角形 ABC の外接円の弧 BC上にないときは,AX < BX + CX が成り立つ。
問題2 三角形 PQR について,各頂点からの距離の和 PY + QY + RY が最小になる点 Y はどのような位置にあるかを求めよ。
(2) 太郎さんと花子さんは問題2について,次のような会話をしている。
花子 : 問題1で証明したことは,二つの線分 BX と CX の長さの和を一つの線分 AX の長さに置き換えられるってことだよね。
太郎 : 例えば,下の図の三角形 PQR で辺 PQ を1辺とする正三角形をかいてみたらどうかな。ただし,辺 QR を最も長い辺とするよ。 辺 PQ に関して点 R とは反対側に点 S をとって,正三角形 PSQ を かき,その外接円をかいてみようよ。
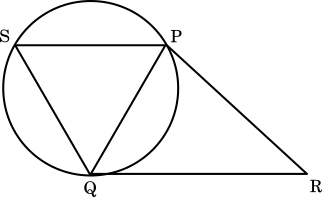
花子 : 正三角形 PSQ の外接円の弧 PQ 上に点 T をとると,PT と QT の長さの和は線分 $\boxed{\text{ ウ }}$ の長さに置き換えられるから,PT + QT + RT = $\boxed{\text{ ウ }}$ + RT になるね。
太郎 : 定理と問題1で証明したことを使うと問題2の点 Y は,点 $\boxed{\text{ エ }}$ と点 $\boxed{\text{ オ }}$ を通る直線と $\boxed{\text{ カ }}$ との交点になることが示せるよ。
花子 : でも,∠QPR が $\boxed{\text{ キ }}\degree$ より大きいときは,点 $\boxed{\text{ エ }}$ と点 $\boxed{\text{ オ }}$ を通る直線と $\boxed{\text{ カ }}$ が交わらないから,∠QPR が $\boxed{\text{ キ }}\degree$ より小さいときという条件がつくよね。
太郎 : では,∠QPR が $\boxed{\text{ キ }}\degree$ より大きいときは,点 Y はどのような点になるのかな。
(2)(i)
$\boxed{\text{ ウ }}$ に当てはまるものを,次の⓪~⑤のうちから一つ選べ。
⓪ PQ ① PS ② QS
③ RS ④ RT ⑤ ST
正解と解説
ウ 5
(1) より PT+QT=ST だから
PT+QT+RT=ST+RT
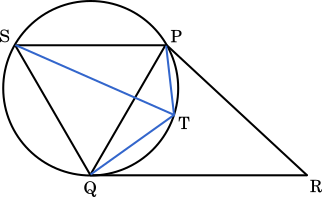
(2)(ii)
$\boxed{\text{ エ }}$,$\boxed{\text{ オ }}$ に当てはまるものを,次の⓪~④ のうちから一つずつ選べ。ただし,$\boxed{\text{ ウ }}$,$\boxed{\text{ オ }}$ の解答の順序は問わない。
⓪ P ① Q ② R ③ S ④ T
正解と解説
(ii) エ,オ 2,3
(2)(iii)
$\boxed{\text{ カ }}$カ に当てはまるものを,次の⓪~⑤のうちから一つ選べ。
⓪ 辺 PR ① 辺 PS ② 辺 QS
③ 弧 PQ ④ 弧 PS ⑤ 弧 QS
正解と解説
(iii) カ 3
(i) の点 T を Y に置き換えて考える。
直線 SR 上に点 Y があるとき,SY+RY は最小になる。
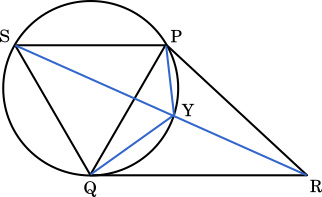
(2)(iv)
$\boxed{\text{ キ }}$ に当てはまるものを,次の⓪~⑥ のうちから一つ選べ。
⓪ 30 ① 45 ② 60 ③ 90
④ 120 ⑤ 135 ⑥ 150
正解と解説
(iv) キ 4
直線 SR が弧 PQ と交わるときの ∠QPR の最大は以下の図のように,点 Y が直線 SR 上にあるとき。
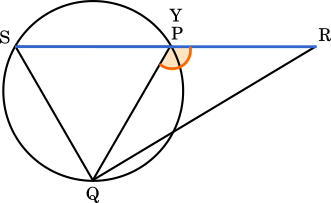
このとき,△PSQ は正三角形で ∠SPQ=60° より ∠QPR=120°
(2)(v)
∠QPR が,$\boxed{\text{ キ }}\degree$ より「小さいとき」と「大きいとき」の点 Y について正しく述べたものを,それぞれ次の⓪~⑥のうちから一つずつ選べ。ただし,同じものを選んでもよい。
小さいとき $\boxed{\text{ ク }}$ 大きいとき $\boxed{\text{ ケ }}$
⓪ 点 Y は,三角形 PQR の外心である。
① 点 Y は,三角形 PQR の内心である。
② 点 Y は,三角形 PQR の重心である。
③ 点 Y は,∠PYR = ∠QYP = ∠RYQ となる点である。
④ 点 Y は,∠PQY + ∠PRY + ∠QPR = 180° となる点である。
⑤ 点 Y は,三角形 PQR の三つの辺のうち,最も短い辺を除く二つの辺の交点である。
⑥ 点 Y は,三角形 PQR の三つの辺のうち,最も長い辺を除く二つの辺の交点である。
正解と解説
(v) ク,ケ 3,6
(Ⅰ) ∠QPR が120°より小さいとき
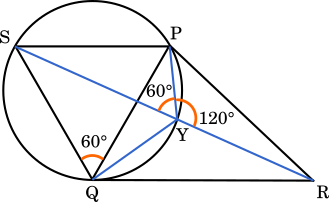
円周角の定理より,∠PQS=∠PYS=60°
また,円に内接する四角形の向かい合う角の和は 180° より
∠PSQ+∠PYQ=180°
60°+∠PYQ=180°
∠PYQ=120°
よって,∠SYQ=60°
したがって,∠PYR=120°,∠QYR=120°となり,∠PYR=∠QYP=∠RYQ が成り立つ。
(Ⅱ) ∠QPR が120°より大きいとき
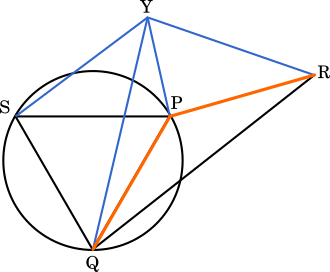
点 Y が弧 PQ 以外にあるとき,[定理] AX<BX+CY より
SY<PY+QY
SY+RY<PY+QY+RY…①
また,点 Y が弧 PQ 上にあるときは SY=PY+QY が成り立つので
SY+RY=PY+QY+RY$\cdots$②
①と②を比較すると,PY+QY+RY が最小となるのは②の方である。よって,点 Y は弧 PQ 上にある。
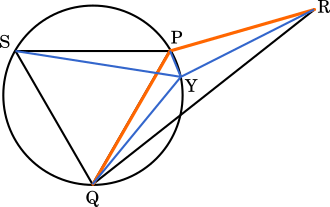
点 Y を弧 PQ 上に置いて考えると,[問題1]の AX=BX+CX より SY=QY+PY が成り立つので
SY+RY=QY+PY+RY
このとき,点 Y が弧 PQ 上の点であるという条件の下,SY+RY が最も短くなる場合を考えると,点 Y が 点 P の位置にあるときである。
SNSでシェア