【スマホで読む・わかりやすい】共通テスト試行H30年度数学IA【解説・正解・問題】
第2問
〔1〕 ∠ACB=90° である直角三角形 ABC と,その辺上を移動する 3 点 P,Q,R がある。点P,Q,R は,次の規則に従って移動する。
・最初,点 P,Q,R はそれぞれ点 A,B,C の位置にあり,点P,Q,R は同時刻に移動を開始する。
・点 P は辺 AC 上を,点 Q は辺 BA 上を,点 R は辺 CB 上を,それぞれ向きを変えることなく,一定の速さで移動する。ただし,点 P は毎秒 1 の速さで移動する。
・点 P,Q,R は,それぞれ点 C,A,B の位置に同時刻に到達し,移動を終了する。
次の問いに答えよ。
(1) 図 1 の直角三角形 ABC を考える。
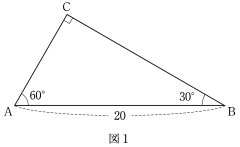
〔1〕(1)(i)
各点が移動を開始してから 2 秒後の線分 PQ の長さと三角形 APQ の面積 S を求めよ。
PQ = $\boxed{\text{ア}}\sqrt{\boxed{\text{イウ}}}$,S = $\boxed{\text{エ}}\sqrt{\boxed{\text{オ}}}$
正解と解説
ア イウ 2 57 エ オ 8 3
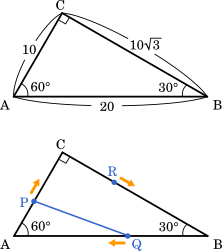
三角形は,各辺の比が $1:2:\sqrt{3}$ の直角三角形だから,AC=10,BC$=10\sqrt{3}$
点 P は毎秒 1 の速さで移動するので,10 秒で C に到達する。よって,点 Q,R も 10 秒でそれぞれ点 A,B に到達する。ここから,点 Q の速さは毎秒 2,点 R の速さは毎秒 $\sqrt{3}$ であることが分かる。
余弦定理より
$\text{PQ}^2=2^2+16^2-2\cdot 2\cdot 16\cos 60\degree$
$=260-64\cdot\cfrac{1}{2}=228$
PQ=$2\sqrt{57}$
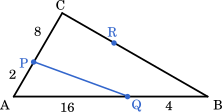
$S=\cfrac{1}{2}\cdot 2\cdot 16\cdot\sin 60\degree$
$=16\cdot\cfrac{\sqrt{3}}{2}=8\sqrt{3}$
〔1〕(1)(ii)
各点が移動する間の線分 PR の長さとして,とり得ない値,一回だけとり得る値,二回だけとり得る値を,次の⓪~④のうちからそれぞれすべて選べ。ただし,移動には出発点と到達点も含まれるものとする。
とり得ない値 カ
一回だけとり得る値 キ
二回だけとり得る値 ク
⓪ $\sqrt{5}$ ① $5\sqrt{3}$ ② $4\sqrt{5}$
③ $10$ ④ $10\sqrt{3}$
正解と解説
カ 0 キ 1,4 ク 2,3
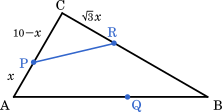
$x$ 秒後における線分PRの長さは,三平方の定理より
$\text{PR}^2=(10-x)^2+(\sqrt{3}x)^2$
展開して整理すると
$=4x^2-20x+100$
式を平方完成すると
$=4\Big(x-\cfrac{5}{2}\Big)^2+75$
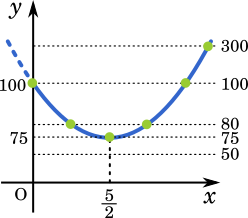
グラフは $\text{PR}^2$ の値であることと,$x$ の範囲 0 ≦ $x$ ≦ 10 に注意する。
各選択肢を2乗すると
⓪ 50 ① 75 ② 80 ③ 100 ④ 300
となる。

グラフとの交点を調べると
⓪ 取りえない
① 一回だけ取り得る
② 二回だけ取り得る
③ 二回だけ取り得る
④ 一回だけ取り得る
〔1〕(1)(iii)
各点が移動する間における三角形 APQ,三角形 BQR,三角形 CRPの面積をそれぞれ $S_1$,$S_2$,$S_3$ とする。各時刻における $S_1$,$S_2$,$S_3$ の間の大小関係と,その大小関係が時刻とともにどのように変化するかを答えよ。解答は,解答欄 (う) に記述せよ。
正解と解説
(う)時刻によらず,$S_1=S_2=S_3$ である。
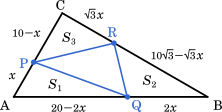
それぞれの三角形の面積を求めると
△APQ$=\cfrac{1}{2}x(20-2x)\sin 60\degree$
△BQR$=\cfrac{1}{2}2x(10\sqrt{3}-\sqrt{3}x)\sin 30\degree$
△CRP$=\cfrac{1}{2}\sqrt{3}x(10-x)$
計算すると,すべて $-\cfrac{\sqrt{3}}{2}x^2+5\sqrt{3}x$
〔1〕(2)
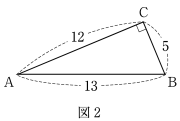
直角三角形 ABC の辺の長さを右の図 2 のように変えたとき,三角形 PQR の面積が 12 となるのは,各点が移動を開始してから何秒後かを求めよ。
$\cfrac{\boxed{\text{ケコ}}\pm\boxed{\text{サ}}\sqrt{\boxed{\text{シ}}}}{\boxed{\text{ス}}}$ 秒後
正解と解説
$\cfrac{\boxed{\text{ケコ}}\pm\boxed{\text{サ}}\sqrt{\boxed{\text{シ}}}}{\boxed{\text{ス}}}$ $\cfrac{30\pm6\sqrt{5}}{5}$ 秒後
△PQR の面積は △ABC から △APQ と △BQR および △CRP の面積を引くことで求められる。
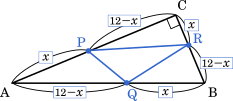
上の図のように,$x$ 秒後でのそれぞれの辺の比はそれぞれ $x:12-x$ となる。
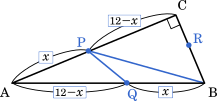
△APQ の面積を求める場合,△ABC を底辺の比で分割して,
△ABP=△ABC$\cdot\cfrac{x}{12}$
△APQ=△ABP$\cdot\cfrac{12-x}{12}$
式をまとめると
△ABP=△ABC$\cdot\cfrac{x}{12}\cdot\cfrac{12-x}{12}$
$=30\cdot\cfrac{x(12-x)}{144}=\cfrac{5x(12-x)}{24}$
同様にして △BQR,△CRP も同じ面積になる。
したがって,△PQR の面積は
△PQR=$30-3\cdot\cfrac{5x(12-x)}{24}$
△PQR の面積が 12 になるとき
$ 30-3\cdot\cfrac{5x(12-x)}{24}=12$
式を整理して
$5x^2-60x+144=0$
$ x=\cfrac{30\pm6\sqrt{5}}{5}$
〔2〕 太郎と花子さんは二つの変量 $x, y$ の相関係数について考えている。二人の会話を読み,下の問いに答えよ。
花子:先生からもらった表計算ソフトの A 列と B 列に値を入れると,E 列には D 列に対応する正しい値が表示されるよ。
太郎:最初は簡単なところで二組の値から考えてみよう。
花子:2 行目を$(x, y)$=(1,2),3行目を$(x, y)$=(2,1)としてみるね。
このときのコンピュータの画面のようすが次の図である。
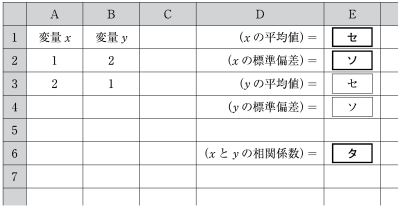
〔2〕(1)
セ,ソ,タに当てはまるものを,次の⓪~⑨のうちから一つずつ選べ。ただし,同じものを繰り返し選んでもよい。
⓪ -1.50 ① -1.00
② -0.50 ③ -0.25
④ 0.00 ⑤ 0.25
⑥ 0.50 ⑦ 1.00
⑧ 1.50 ⑨ 2.00
正解と解説
セ 8 ソ 6 タ 1
$x$ の平均値は
$\cfrac{1+2}{2}=1.50$
$x$ の分散を求めると
$s^2=\cfrac{(1-1.50)^2+(2-1.50)^2}{2}=0.25$
よって,標準偏差は
$ s=\sqrt{0.25}=\sqrt{\cfrac{1}{4}}=\cfrac{1}{2}=0.5$
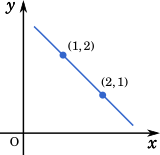
上の図のように直線を引いてみると,2つの点は直線上にある。データに散らばりがないので,相関係数は 1 である。
太郎:3 行目の変量 $y$ の値を 0 や -1 に変えても相関係数の値は タ になったね。
花子:今度は,3 行目の変量 $y$ の値を 2 に変えてみよう。
太郎:エラーが表示されて,相関係数は計算できないみたいだ。
〔2〕(2)
変量 $x$ と変量 $y$ の値の組を変更して,$(x,y)=(1,2),(2,2)$ としたときには相関係数が計算できなかった。その理由として最も適当なものを,次の⓪~③のうちから一つ選べ。チ
⓪ 値の組の個数が2個しかないから。
① 変量 $x$ の平均値と変量 $y$ の平均値が異なるから。
② 変量 $x$ の標準偏差の値と変量 $y$ の標準偏差の値が異なるから。
③ 変量 $y$ の標準偏差の値が 0 であるから。
解答・解説
チ 3
標準偏差が 0 であれば上の式の分母も 0 になり,計算できない。
花子:3 行目の変量 $y$ の値を 3 に変更してみよう。相関係数の値は 1.00 だね。
太郎:3 行目の変量 $y$ の値が 4 のときも 5 のときも,相関係数の値は 1.00 だ。
花子:相関係数の値が 1.00 になるのはどんな特徴があるときかな。
太郎:値の組の個数を多くすると何かわかるかもしれないよ。
花子:じゃあ,次に値の組の個数を 3 としてみよう。
太郎:$(x, y)$=(1, 1),(2, 2),(3, 3) とすると相関係数の値は 1.00 だ。
花子:$(x, y)$=(1, 1),(2, 2),(3, 1) とすると相関係数の値は 0.00 になった。
太郎:$(x, y)$=(1, 1),(2, 2),(2, 2) とすると相関係数の値は 1.00 だね。
花子:まったく同じ値の組が含まれていても相関係数の値は計算できることがあるんだね。
太郎:思い切って,値の組の個数を 100 にして,1 個だけ $(x, y)$=(1, 1) で,99 個は $(x, y)$=(2, 2) としてみるね……。相関係数の値は 1.00 になったよ。
花子:値の組の個数が多くても,相関係数の値が 1.00 になるときもあるね。
〔2〕(3)
相関係数の値についての記述として誤っているものを,次の⓪~④のうちから一つ選べ。ツ
⓪ 値の組の個数が 2 のときには相関係数の値が 0.00 になることはない。
① 値の組の個数が 3 のときには相関係数の値が -1.00 となることがある。
② 値の組の個数が4のときには相関係数の値が 1.00 となることはない。
③ 値の組の個数が 50 であり,1個の値の組が $(x, y)$=(1, 1),残りの 49 個の値の組が$(x, y)$=(2, 0) のときは相関係数の値は -1.00 である。
④ 値の組の個数が 100 であり,50個の値の組が $(x, y)$=(1, 1),残りの 50 個の値の組が$(x, y)$=(2, 2) のときは相関係数の値は 1.00 である。
正解と解説
ツ 2
問題文の議論を踏まえると,値がすべて一直線上に並んでいるなら相関係数は 1.00 か -1.00 である。値の組の個数が 2 のときは,相関係数は 1.00 か -1.00 か,計算できないかである。また,値の組の個数が 3 以上の場合,相関係数が 0.00 になることがある。
⓪ 値の組の個数が 2 のときには,相関係数は 1.00 になるか,計算できないかのどちらかである。よって正しい。
① 例えば $(x,y)$=(1,2),(2,1),(2,1) とすると相関係数の値は -1.00 になる。よって正しい。
② 例えば $(x,y)$=(1,1),(2,2),(2,2),(2,2) とすると相関係数の値は 1.00 になる。よって誤り。
③ 正しい。
④ 正しい。
花子:値の組の個数が 2 のときは,相関係数の値は 1.00 かタ,または計算できない場合の3 通りしかないね。
太郎:値の組を散布図に表したとき,相関係数の値はあくまで散布図の点が,テ 程度を表していて,値の組の個数が 2 の場合に,花子さんが言った 3 通りに限られるのは ト からだね。値の組の個数が多くても値の組が 2 種類のときはそれらにしかならないんだね。
花子:なるほどね。相関係数は,そもそも値の組の個数が多いときに使われるものだから,組の個数が極端に少ないときなどにはあまり意味がないのかもしれないね。
太郎:値の組の個数が少ないときはもちろんのことだけど,基本的に散布図と相関係数を合わせてデータの特徴を考えるとよさそうだね。
〔2〕(4)
テ,ト に当てはまる最も適当なものを,次の各解答群のうちから一つずつ選べ。
テの解答群
⓪ $x$ 軸に関して対称に分布する
① 変量 $x,y$ のそれぞれの中央値を表す点の近くに分布する
② 変量 $x,y$ のそれぞれの平均値を表す点の近くに分布する
③ 円周に沿って分布する
④ 直線に沿って分布する
トの解答群
⓪ 変量 $x$ の中央値と平均値が一致する
① 変量 $x$ の四分位数を考えることができない
② 変量 $x, y$ のそれぞれの平均値を表す点からの距離が等しい
③ 平面上の異なる 2 点は必ずある直線上にある
④ 平面上の異なる 2 点を通る円はただ 1 つに決まらない
正解と解説
テ 4 ト 3
散布図では点の分布の様子が1つの直線に接近しているほど相関が強いという。
SNSでシェア