【スマホで読む・わかりやすい】共通テスト試行H30年度数学IA【解説・正解・問題】
第1問
〔1〕 有理数全体の集合を $A$,無理数全体の集合を $B$ とし,空集合 $\varnothing$ と表す。このとき,次の問いに答えよ。
〔1〕(1)
「集合 $A$ と集合 $B$ の共通部分は空集合である」という命題を,記号を用いて表すと次のようになる。
$A\cap B=\varnothing$
「1 のみを要素にもつ集合は集合 $A$ の部分集合である」という命題を,記号を用いて表せ。解答は,解答欄(あ)に記述せよ。
(2) 命題「$x$∈$B$,$y$∈$B$ ならば,$x+y$∈$B$ である」が偽であることを示すための反例となる $x,y$ の組を,次の⓪~⑤のうちから二つ選べ。必要ならば,$\sqrt{2},\space \sqrt{3},\space \sqrt{2}+\sqrt{3}$ が無理数であることを用いてもよい。ただし,解答の順序は問わない。ア,イ
⓪ $x=\sqrt{2},\space y=0$
① $x=3-\sqrt{3},\space y=\sqrt{3}-1$
② $x=\sqrt{3}+1,\space y=\sqrt{2}-1$
③ $x=\sqrt{4},\space y=-\sqrt{4}$
④ $x=\sqrt{8},\space y=1-2\sqrt{2}$
⑤ $x=\sqrt{2}-2,\space y=\sqrt{2}+2$
正解と解説
(あ) $\{1\}\subset A$
ア,イ 1,4
「$x$∈$B$,$y$∈$B$ ならば,$x+y$∈$B$ である」は,言い換えると「$x,y$ が無理数なら $x+y$ も無理数」である。反例を見つけるために,$x+y$ が有理数となる場合を選ぶ。
① $x+y=3-\sqrt{3}+\sqrt{3}-1=2\cdots$有理数
③ $x=\sqrt{4}=2$,つまり有理数であり,$x$ が無理数という条件に当てはまらない。
④ $\sqrt{8}=2\sqrt{2}$ だから,
$x+y=2\sqrt{2}+1-2\sqrt{2}=1\cdots$有理数
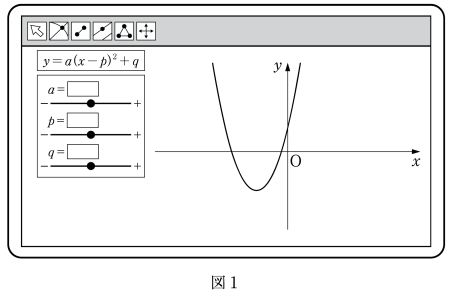
〔2〕 関数 $f(x)=a(x-p)^2+q$ について,$y=f(x)$ のグラフをコンピュータのグラフ表示ソフトを用いて表示させる。
このソフトでは,$a$,$p$,$q$ の値を入力すると,その値に応じたグラフが表示される。さらに,それぞれの の下にある ● を左に動かすと値が減少し,右に動かすと値が増加するようになっており,値の変化に応じて関数のグラフが画面上で変化する仕組みになっている。
最初に,$a$,$p$,$q$ をある値に定めたところ,図 1 のように,$x$ 軸の負の部分と 2 点で交わる下に凸の放物線が表示された。
〔2〕(1)
図 1 の放物線を表示させる $a$,$p$,$q$ の値に対して,方程式 $f(x)=0$ の解について正しく記述したものを,次の⓪~④のうちから一つ選べ。 ウ
⓪ 方程式 $f(x)=0$ は異なる二つの正の解を持つ。
① 方程式 $f(x)=0$ は異なる二つの負の解を持つ。
② 方程式 $f(x)=0$ は正の解と負の解を持つ。
③ 方程式 $f(x)=0$ は重解を持つ。
④ 方程式 $f(x)=0$ は実数解を持たない。
正解と解説
ウ 1
グラフが $x$ 軸と交わる点が $f(x)=0$ の解である。グラフを見ると,2 点とも $x$ 軸の負の側で交わっているので,二つの負の解を持つ。
〔2〕(2)
次の操作A,操作P,操作Qのうち,いずれか一つの操作を行い,不等式 $f(x)$>$0$ の解を考える。
操作A:図1の状態から $p$,$q$ の値は変えず,$a$ の値だけを変化させる。
操作P:図1の状態から $a$,$q$ の値は変えず,$p$ の値だけを変化させる。
操作Q:図1の状態から $a$,$p$ の値は変えず,$q$ の値だけを変化させる。
このとき,操作A,操作P,操作Qのうち,「不等式 $f(x)$ > 0 の解がすべての実数となること」が起こり得る操作は エ。また,「不等式 $f(x)$ > 0 の解がないこと」が起こり得る操作は オ。
エ,オ に当てはまるものを,次の⓪~⑦のうちから一つずつ選べ。ただし,同じものを選んでもよい。
⓪ ない
① 操作Aだけである
② 操作Pだけである
③ 操作Qだけである
④ 操作Aと操作Pだけである
⑤ 操作Aと操作Qだけである
⑥ 操作Pと操作Qだけである
⑦ 操作Aと操作Pと操作Qのすべてである
—
正解と解説
エ 3 オ 1
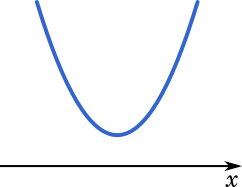
不等式 $f(x)$> 0 の解がすべての実数であるとき,関数のグラフは $x$ 軸の上にあり,$x$軸と接しない。こうしたグラフを作るためにはもとのグラフを上に移動させるとよいので,$q$ の値を変化させることになる。
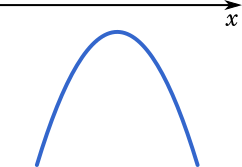
不等式 $f(x)$ > 0 の解がないとき,関数のグラフは $x$ 軸の下側にある。こうしたグラフを作るためには $a$ が負の値であればよいので,$a$ の値を変化させることになる。
〔3〕

久しぶりに小学校に行くと,階段の一段一段の高さが低く感じられることがある。これは,小学校と高等学校とでは階段の基準が異なるからである。学校の階段の基準は,下のように建築基準法によって定められている。
高等学校の階段では,蹴上げが 18cm 以上,踏面が 26cm 以上となっており,この基準では,傾斜は最大で約 35° である。
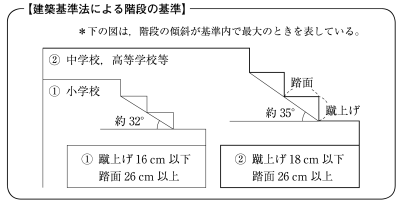
階段の傾斜をちょうど 33° とするとき,蹴上げを 18cm 以下にするためには,踏面をどのような範囲に設定すればよいか。踏面を $x$cm として,$x$ のとり得る値の範囲を求めるための不等式を,33° の三角比と $x$ を用いて表せ。解答は,解答欄(い) に記述せよ。ただし,踏面と蹴上げの長さはそれぞれ一定であるとし,また,踏面は水平であり,蹴上げは踏面に対して垂直であるとする。
(本問題の図は,「建築基準法の階段に係る基準について」(国土交通省)をもとに作成している。)
正解と解説
(い) $26$ ≦ $x$ ≦ $\cfrac{18}{\tan33\degree}$
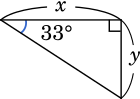
踏面を $x$,蹴上げを $y$ とすると,問題文より
$x$ ≧ $26\cdots$①
0 ≦ $y$ ≦ 18 $\cdots$②
である。上の図より
$\cfrac{y}{x}=\tan 33\degree$
$y=x\tan 33\degree$
②に代入して
0 ≦ $x\tan 33\degree$ ≦ 18
0 ≦ $x$ ≦ $\cfrac{18}{\tan 33\degree}\cdots$③
①,③より
26 ≦ $x$ ≦ $\cfrac{18}{\tan 33\degree}$
※解答としてはこれで良いが,本来 26 < $\cfrac{18}{\tan 33\degree}$ であることを確認する必要がある。
$\tan 35\degree\fallingdotseq\cfrac{18}{26}$ であることを利用して
$\tan 33\degree$ < $\tan 35\degree$ だから
$\tan 33\degree$ < $\cfrac{18}{26}$
$\cfrac{\tan 33\degree}{18}$ < $\cfrac{1}{26}$
$\cfrac{18}{\tan 33\degree}$ > 26
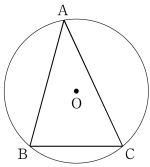
〔4〕 三角形 ABC の外接円を O とし,円 O の半径を $R$ とする。辺 BC,CA,AB の長さをそれぞれ $a$,$b$,$c$ とし,∠CAB,∠ABC,∠BCA の大きさをそれぞれ $A$,$B$,$C$ とする。
太郎さんと花子さんは三角形 ABC について
$\cfrac{a}{\sin A}=\cfrac{b}{\sin B}=\cfrac{c}{\sin C}=2R\cdots\cdots$(*)
の関係が成り立つことを知り,その理由について,まず直角三角形の場合を次のように考察した。
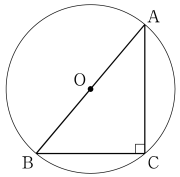
$C=90\degree$ のとき,円周角の定理より,線分 AB は円 O の直径である。よって
$\sin A=\cfrac{\text{BC}}{\text{AB}}=\cfrac{a}{2R}$
だから
$\cfrac{a}{\sin A}=2R$
同様にして
$\cfrac{b}{\sin B}=2R$
である。また,$\sin C=1$ より
$\cfrac{c}{\sin C}=2R$
よって,$C=90\degree$ のとき(*)の関係が成り立つ。
次に,太郎さんと花子さんは,三角形 ABC が鋭角三角形や鈍角三角形のときにも(*)の関係が成り立つことを証明しようとしている。
〔4〕(1)
三角形 ABC が鋭角三角形の場合についても(*)の関係が成り立つことは,直角三角形の場合に(*)の関係が成り立つことをもとにして,次のような太郎さんの構想により証明できる。
太郎さんの証明の構想
点 A を含む弧 BC 上に点 A’ をとると,円周角の定理より
∠CAB = ∠CA’B
が成り立つ。
特に,カ を点 A’ とし,三角形 A’BC に対して $C=90\degree$ の場合の考察の結果を利用 すれば,
$\cfrac{a}{\sin A}=2R$
が成り立つことを証明できる。
$\cfrac{b}{\sin B}=2R$,$\cfrac{c}{\sin C}=2R$ についても同様に証明できる。
カに当てはまる最も適当なものを,次の①~④のうちから一つ選べ。
⓪ 点 B から辺 AC に下ろした垂線と,円 O との交点のうち点 B と異なる点
① 直線 BO と円 O との交点のうち点 B と異なる点
② 点 B を中心とし点Cを通る円と,円 O との交点のうち点 C と異なる点
③ 3 点 O を通り辺 BC に平行な直線と,円 O との交点のうちの一つ
④ 辺 BC と直交する円 O の直径と,円 O との交点のうちの一つ
正解と解説
カ 1
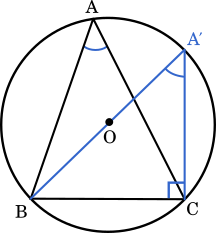
円周角の定理より∠A=∠A’
また,線分 A’B が円の中心を通る(線分 A’B が直径)のとき,円周角は 90° となるので,∠A’CB=90°。
こうして,直角三角形の場合と同じになるので,(*)が成り立つ。
〔4〕(2)
三角形 ABC が $A$ > 90° である鈍角三角形の場合についても $\cfrac{a}{\sin A}=2R$ が成り立つことは,次のような花子さんの構想により証明できる。
花子さんの証明の構想
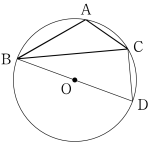
右図のように,線分 BD が円 O の直径となるように点 D をとると,三角形 BCD において
$\sin$キ$=\cfrac{a}{2R}$
である。
このとき,四角形 ABDC は円 O に内接するから,
∠CAB = ク
であり,
$\sin\text{∠CAB}=\sin($ク$)=\sin$キ
となることを用いる。
キ,クに当てはまるものを,次の各解答群のうちから一つずつ選べ。
キの解答群
⓪ ∠ABC ① ∠ABD ② ∠ACB
③ ∠ACD ④ ∠BCD ⑤ ∠BDC
⑥ ∠CBD
クの解答群
⓪ $90\degree+$∠ABC ① $180\degree-$∠ABC
② $90\degree+$∠ACB ③ $180\degree-$∠ACB
④ $90\degree+$∠BDC ⑤ $180\degree-$∠BDC
⑥ $90\degree+$∠ABD ⑦ $180\degree-$∠CBD
正解と解説
キ 5 ク 5
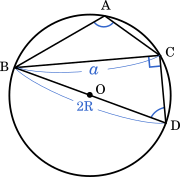
辺 BD が直径となるので,∠BCD=90°。よって,三角形 BCD は直角三角形であることに注意して,円周角の定理より
∠CAB+∠BDC=180°
円に内接する四角形の向かい合う角の大きさの合計は 180°だから
∠CAB=180°-∠BDC
よって,$\sin(180\degree-x)=\sin x$ より
$\sin\text{∠CAB}=\sin\text{∠BDC}$
SNSでシェア