【スマホで読む・わかりやすい】共通テスト試行H29年度数学IIB【解説・正解・問題】
第1問
〔 1 〕
$a$ を定数とする。座標平面上に,原点を中心とする半径 $5$ の円 $C$ と,直線 $\ell : x + y = a$ がある。
$C$ と $\ell$ が異なる $2$ 点で交わるための条件は,$-\boxed{\text{ ア }}\sqrt{\boxed{\text{ イ }}}$<$a$<$\boxed{\text{ ア }}\sqrt{\boxed{\text{ イ }}}\space\cdots$①である。①の条件を満たすとき,$C$ と $\ell$ の交点の一つを $\text{P}(s,t)$ とする。このとき,$st=\cfrac{a^2-\boxed{\text{ ウエ }}}{\boxed{\text{ オ }}}$である。
正解と解説
$\boxed{\text{ ア }}$,$\boxed{\text{ イ }}$ $5$,$2$
$\boxed{\text{ ウエ }}$,$\boxed{\text{ オ }}$ $25$,$2$
$C:x^2+y^2=25\cdots$①
$\ell:x+y=a\cdots$②
②を変形して
$y=-x+a$
両辺を2乗して
$y^2=(-x+a)^2=x^2-2ax+a^2$
①に代入
$x^2+x^2-2ax+a^2=25$
$2x^2-2ax+a^2-25=0$
異なる2点で交わるという条件から,判別式を求めると
$\cfrac{D}{4}=a^2-2a^2+50>0$
$-a^2+50>0$
$a^2-50<0$
$(a+5\sqrt{2})(a-5\sqrt{2})<0$
したがって
$-5\sqrt{2}$ < $a$ < $5\sqrt{2}$
②を2乗すると
$x^2+2xy+y^2=a^2\cdots$③
①を③に代入すると
$2xy+25=a^2$
$ xy=\cfrac{a^2-25}{2}$
$(x,y)$が$(s,t)$のとき
$st=\cfrac{a^2-25}{2}$
〔 2 〕
$a$ を $1$ でない正の実数とする。(i)〜(iii)のそれぞれの式について,正しいものを,下の ⓪ 〜 ③ のうちから一つずつ選べ。ただし,同じものを繰り返し選んでもよい。
(i) $\sqrt[4]{a^3}\times a^{\small{\frac{2}{3}}}=a^2$ $\boxed{\text{ カ }}$
(ii) $\cfrac{(2a)^6}{(4a)^2}=\cfrac{a^3}{2}$ $\boxed{\text{ キ }}$
(iii) $4(\log_2 a-\log_4 a)=\log_{\sqrt{2}} a$ $\boxed{\text{ ク }}$
⓪ 式を満たす $a$ の値は存在しない。
① 式を満たす $a$ の値はちょうど一つである。
② 式を満たす $a$ の値はちょうど二つである。
③ どのような $a$ の値を代入しても成り立つ式である。
正解と解説
$\boxed{\text{ カ }}$,$\boxed{\text{ キ }}$,$\boxed{\text{ ク }}$ ⓪,①,③
(i)
$\sqrt[4]{a^3}\times a^{\small{\frac{2}{3}}}=a^2$
$a^{\small{\frac{3}{4}}}\times a^{\small{\frac{2}{3}}}=a^2$
$a^{\small{\frac{3}{4}+\frac{2}{3}}}=a^2$
$a^{\small{\frac{17}{12}}}=a^2$
$a^{17}=a^{24}$
両辺を$a^{17}$で割ると
$1=a^7$
$a=1$
$a\not=1$より不適。
(ii)
$\cfrac{(2a)^6}{(4a)^2}=\cfrac{a^3}{2}$
$\cfrac{64a^6}{16a^2}=\cfrac{a^3}{2}$
$4a^4=\cfrac{a^3}{2}$
$a=\cfrac{1}{8}$
式を満たす$a$の値は一つに定まる。
(iii)
底を2に合わせていくとよい
$4(\log_2 a-\log_4 a)=\log_{\sqrt{2}}a$
$4\Big(\log_2 a-\cfrac{\log_2 a}{\log_2 4}\Big)=\cfrac{\log_2 a}{\log_2 \sqrt{2}}$
$4\Big(\log_2 a-\cfrac{\log_2 a}{2}\Big)=\cfrac{\log_2 a}{\log_2 2^{\small{\frac{1}{2}}}}$
$4\log_2 a-2\log_2 a=\cfrac{\log_2 a}{\cfrac{1}{2}\log_2 2}$
$2\log_2 a=\cfrac{\log_2 a}{\cfrac{1}{2}}$
$2\log_2 a=2\log_2 a$
$a$にどのような値を代入しても恒等式が成立する。
〔 3 〕(1)
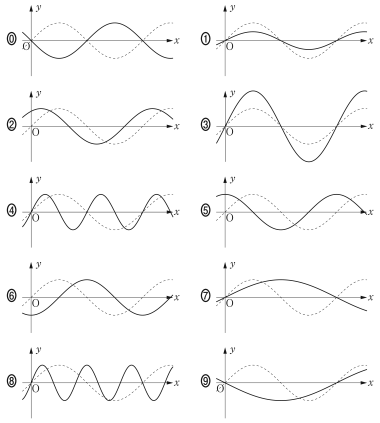
下の図の点線は $y=\sin x$ のグラフである。(i),(ii)の三角関数のグラフが実線で正しくかかれているものを,下の ⓪ 〜 ⑨ のうちから一つずつ選べ。ただし,同じものを選んでもよい。
(i) $y=\sin{2x}$ $\boxed{\text{ ケ }}$
(ii) $y=\sin\Big(x+\cfrac{3}{2}\pi\Big)$ $\boxed{\text{ コ }}$
正解と解説
$\boxed{\text{ ケ }}$,$\boxed{\text{ コ }}$ ④,⑥
$y=\sin{2x}$ は周期が2倍になったグラフであり,④が正しい。
$y=\sin\Big(x+\cfrac{3}{2}\pi\Big)$ は $y=\sin x$ のグラフを $x$ 軸方向に $-\cfrac{3}{2}\pi$ 平行移動したものであり,⑥が正しい。
〔3〕(2)
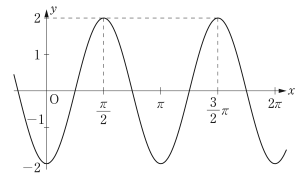
次の図はある三角関数のグラフである。その関数の式として正しいものを,下の ⓪ 〜 ⑦ のうちからすべて選べ。 $\boxed{\text{ サ }}$
⓪ $y=2\sin\Big(2x+\cfrac{\pi}{2}\Big)$
① $y=2\sin\Big(2x-\cfrac{\pi}{2}\Big)$
② $y=2\sin 2\Big(x+\cfrac{\pi}{2}\Big)$
③ $y=\sin 2\Big(2x-\cfrac{\pi}{2}\Big)$
④ $y=2\cos \Big(2x+\cfrac{\pi}{2}\Big)$
⑤ $y=2\cos 2\Big(x-\cfrac{\pi}{2}\Big)$
⑥ $y=2\cos 2\Big(x+\cfrac{\pi}{2}\Big)$
⑦ $y=\cos 2\Big(2x-\cfrac{\pi}{2}\Big)$
正解と解説
$\boxed{\text{ サ }}$ ①,⑤,⑥
グラフの頂点の $y$ 座標が $2$ であることから,③,⑦は除くとよい。その上で,選択肢より$+$方向と,$-$方向に平行移動した場合を考えるとよい。
示されたグラフは,$2\sin 2x$ のグラフを $ +\cfrac{\pi}{4}$ 移動したものである。式で表すと $y=2\sin 2\Big(x-\cfrac{\pi}{4}\Big)=2\sin\Big(2x-\cfrac{\pi}{2}\Big)$ となり,①が適する。
また,グラフを $+\cfrac{5pi}{4}$ 移動しても,もとのグラフと一致するが,これは $-\cfrac{3\pi}{4}$ と同じことである。しかし,式で表すと $y=2\sin 2\Big(x+\cfrac{3\pi}{4}\Big)=2\sin\Big(2x-\cfrac{3\pi}{2}\Big)$ となり,当てはまる選択肢はない。
次に,グラフは $2\cos 2x$ のグラフを $+\cfrac{\pi}{2}$ 移動したものである。式で表すと $y=2\cos 2\Big(x-\cfrac{\pi}{2}\Big)$ となり,⑤が適する。また,グラフを $+\cfrac{3\pi}{2}$ 移動しても,もとのグラフと一致するが,これは $-\cfrac{\pi}{2}$ と同じことである。式で表すと $y=2\cos 2\Big(x+\cfrac{\pi}{2}\Big)$ となり,⑥が適する。
〔 4 〕 先生と太郎さんと花子さんは,次の問題とその解答について話している。 三人の会話を読んで,下の問いに答えよ。
【問題】
$x,y$ を正の実数とするとき,$\Big(x+\cfrac{1}{y}\Big)\Big(y+\cfrac{4}{x}\Big)$ の最小値を求めよ。
【解答 A】
$x>0$,$\cfrac{1}{y}>0$ であるから,相加平均と相乗平均の関係により
$x+\cfrac{1}{y}\geqq 2\sqrt{x\cdot\cfrac{1}{y}}=2\sqrt{\cfrac{x}{y}}$・・・・・・①
$y>0$,$\cfrac{4}{x}>0$ であるから,相加平均と相乗平均の関係により
$y+\cfrac{4}{x}\geqq 2\sqrt{y\cdot\cfrac{4}{x}}=\sqrt{\cfrac{y}{x}}$・・・・・・②
である。①,②の両辺は正であるから,
$\Big(x+\cfrac{1}{y}\Big)\Big(y+\cfrac{4}{x}\Big)\geqq 2\sqrt{\cfrac{x}{y}}\cdot 4\sqrt{\cfrac{y}{x}}=8$
よって,求める最小値は$8$である。
【解答 B】
$\Big(x+\cfrac{1}{y}\Big)\Big(y+\cfrac{4}{x}\Big)=xy+\cfrac{4}{xy}+5$
であり,$xy>0$ であるから,相加平均と相乗平均の関係により
$xy+\cfrac{4}{xy}\geqq 2\sqrt{xy\cdot\cfrac{4}{xy}}=4$
$xy+\cfrac{4}{xy}+5\geqq 4+5=9$
よって,求める最小値は 9 である。
先生 「同じ問題なのに,解答 A と解答 B で答えが違っていますね。」
太郎 「計算が間違っているのかな。」
花子 「いや,どちらも計算は間違えていないみたい。」
太郎 「答えが違うということは,どちらかは正しくないということだよね。」
先生 「なぜ解答 A と解答 B で違う答えが出てしまったのか,考えてみましょう。」
花子 「実際に $x$ と $y$ に値を代入して調べてみよう。」
太郎 「例えば $x=1$,$y=1$ を代入してみると,$\Big(x+\cfrac{1}{y}\Big)\Big(y+\cfrac{4}{x}\Big)$ の値は $2\times 5$ だから $10$ だ。」
花子 「$x=2$,$y=2$ のときの値は $\cfrac{5}{2}\times 4=10$ になった。」
太郎 「$x=2$,$y=1$ のときの値は $3\times 3=9$ になる。」
(太郎と花子,いろいろな値を代入して計算する)
花子 「先生,ひょっとして $\boxed{\text{ シ }}$ ということですか。」
先生 「そのとおりです。よく気づきましたね。」
花子 「正しい最小値は $\boxed{\text{ ス }}$ ですね。」
〔4〕(1)
$\boxed{\text{ シ }}$ に当てはまるものを,次の ⓪ 〜 ③ のうちから一つ選べ。
⓪ $xy+\cfrac{4}{xy}=4$ を満たす $x,y$ の値がない
① $x+\cfrac{1}{y}=2\sqrt{\cfrac{x}{y}}$ かつ $xy+\cfrac{4}{xy}=4$ を満たす $x,y$ の値がある
② $x+\cfrac{1}{y}=2\sqrt{\cfrac{x}{y}}$ かつ $y+\cfrac{4}{x}= 4\sqrt{\cfrac{y}{x}}$ を満たす $x,y$ の値がない
③ $x+\cfrac{1}{y}=2\sqrt{\cfrac{x}{y}}$ かつ $y+\cfrac{4}{x}= 4\sqrt{\cfrac{y}{x}}$ を満たす $x,y$ の値がある
正解と解説
$\boxed{\text{ シ }}$ ②
選択肢を順番に検討していく。共通テストにおいては常に仮説に対する検証のプロセスを重視することが肝要である。
⓪ $xy+\cfrac{4}{xy}=4$ を満たす $x,y$ の値がない
実際に計算をしてみるとよい。
$xy+\cfrac{4}{xy}=4$
両辺に $xy$ をかけて
$x^2 y^2+4=4xy$
$x^2 y^2-4xy+4=0$
$(xy-2)^2=0$
$xy=2$
したがって,式に当てはまる $x$,$y$ が存在するので,不適。(例えば $x=1$,$y=2$ など)
① $x+\cfrac{1}{y}=2\sqrt{\cfrac{x}{y}}$ かつ $xy+\cfrac{4}{xy}=4$ を満たす $x,y$ の値がある
解答Aと解答Bの式が混ざっており,意味を成さない。
② $x+\cfrac{1}{y}=2\sqrt{\cfrac{x}{y}}$ かつ $y+\cfrac{4}{x}=4\sqrt{\cfrac{y}{x}}$ を満たす $x,y$ の値がない
$x+\cfrac{1}{y}=2\sqrt{\cfrac{x}{y}}$
両辺を2乗して
$\Big(x+\cfrac{1}{y}\Big)^2=\Big(2\sqrt{\cfrac{x}{y}}\Big)^2$
$x^2+2\cfrac{x}{y}+\cfrac{1}{y^2}=4\cfrac{x}{y}$
$x^2-2\cfrac{x}{y}+\cfrac{1}{y^2}=0$
$\Big(x-\cfrac{1}{y}\Big)^2=0$
$x=\cfrac{1}{y}$
$xy=1$・・・①
また
$y+\cfrac{4}{x}=4\sqrt{\cfrac{y}{x}}$
両辺を2乗して
$y^2+8\cfrac{y}{x}+\cfrac{16}{x^2}=16\cfrac{y}{x}$
$y^2-8\cfrac{y}{x}+\cfrac{16}{x^2}=0$
$\Big(y-\cfrac{4}{x}\Big)^2=0$
$y=\cfrac{4}{x}$
$xy=4$・・・②
①,②を同時に満たす $x$,$y$ の組は存在しない。よって,適する。
③は,②より不適。
〔4〕(2)
$\boxed{\text{ ス }}$ に当てはまる数を答えよ。
正解と解説
$\boxed{\text{ シ }}$ 9
(1) の結果より,解答Aは誤りである。したがって,解答Bが正しい。
SNSでシェア