【スマホで読む・わかりやすい】共通テスト試行H29年度数学IIB【解説・正解・問題】

第３問

次の文章を読んで，下の問いに答えよ。

ある薬 D を服用したとき，有効成分の血液中の濃度(血中濃度)は一定の割合で減少し，$T$ 時間が経過すると $\cfrac{1}{2}$ 倍になる。薬 D を 1 錠服用すると，服用直後の血中濃度は $P$ だけ増加する。時間 $0$ で血中濃度が $P$ であるとき，血中濃度の変化は次のグラフで表される。適切な効果が得られる血中濃度の最小値を $M$，副作用を起こさない血中濃度の最大値を $L$ とする。

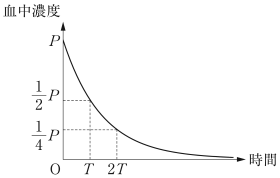
薬 D については，$M = 2$，$L = 40$，$P = 5$，$T = 12$ である。

(1)

薬 D について，12 時間ごとに 1 錠ずつ服用するときの血中濃度の変化は次のグラフのようになる。

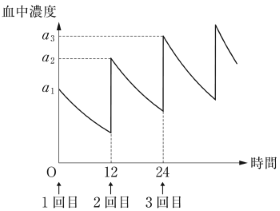
$n$ を自然数とする。$a_n$ は $n$ 回目の服用直後の血中濃度である。$a_1$ は $P$ と一致すると考えてよい。第$(n + 1)$回目の服用直前には，血中濃度は第 $n$ 回目の服用直後から時間の経過に応じて減少しており，薬を服用した直後に血中濃度が $P$ だけ上昇する。この血中濃度が $a_{n+1}$ である。

$P = 5$，$T = 12$ であるから，数列 ${a_n}$ の初項と漸化式は$a_1 = \boxed{\text{ ア }}$，$ a_{n + 1} = \cfrac{\boxed{\text{ イ }}}{\boxed{\text{ ウ }}}a_n+\boxed{\text{ エ }}$　$(n=1,2,3,\cdots)$となる。

数列 ${a_n}$ の一般項を求めてみよう。

【考え方 1 】

数列 ${a_n-d}$，が等比数列となるような定数 $d$ を求める。$d=\boxed{\text{ オカ }}$ に対して，数列 ${a_n-d}$ が公比 $\cfrac{\boxed{\text{ キ }}}{\boxed{\text{ ク }}}$の等比数列になることを用いる。

【考え方 2 】

階差数列をとって考える。数列 ${a_{n + 1}-a_n}$ が公比 $\cfrac{\boxed{\text{ ケ }}}{\boxed{\text{ コ }}}$ の等比数列になることを用いる。

いずれの考え方を用いても，一般項を求めることができ，$a_n=\boxed{\text{ サシ }}-\boxed{\text{ ス }}\bigg(\cfrac{\boxed{\text{ セ }}}{\boxed{\text{ ソ }}}\bigg)^{n-1}$　$(n=1,2,3,\cdots)$である。

---

正解と解説

$\boxed{\text{ ア }}$，$\boxed{\text{ イ }}$，$\boxed{\text{ ウ }}$，$\boxed{\text{ エ }}$　$5$，$1$，$2$，$5$

$\boxed{\text{ オカ }}$，$\boxed{\text{ キ }}$，$\boxed{\text{ ク }}$　$10$，$1$，$2$

$\boxed{\text{ ケ }}$，$\boxed{\text{ コ }}$　$1$，$2$

$\boxed{\text{ サシ }}$，$\boxed{\text{ ス }}$，$\boxed{\text{ セ }}$，$\boxed{\text{ ソ }}$　$10$，$5$，$1$，$2$

$P=5$，$T=12$ より初め血中濃度は $5$ になり，12時間後にはその $\cfrac{1}{2}$ となる。そこで再び服薬すると血中濃度が $5$ 増える。ここから再び服薬したときの血中濃度は $ 5\times\cfrac{1}{2}+5$ であることが分かる。これを漸化式で表すと

$a_1=5$，$a_{n+1}=\cfrac{1}{2}a_n+5$　$(n=1,2,3,\cdots)$

となる。

次に一般項を求める。

【考え方1】のように等比数列を用いる場合は，特性方程式を用いるとよい。

$a_{n+1}=\cfrac{1}{2}a_n+5\cdots$①$\alpha=\cfrac{1}{2}\alpha+5\cdots$②

①－②

$a_{n+1}-\alpha=\cfrac{1}{2}(a_n-\alpha)$

ここで，$\alpha=\cfrac{1}{2}\alpha+5$ より $\alpha=10$ となるので

$a_{n+1}-10=\cfrac{1}{2}(a_n-10)$

$b_n=a_n-10$ とおくと

$b_{n+1}=\cfrac{1}{2}b_n$

また，$b_1=a_1-10=5-10=-5$

数列 ${b_n}$ は初項 $-5$，公比 $\cfrac{1}{2}$ の等比数列だから，一般項は

$b_n=-5\Big(\cfrac{1}{2}\Big)^{n-1}$

$b_n=a_n-10$ を代入して

$a_n-10=-5\Big(\cfrac{1}{2}\Big)^{n-1}$
$a_n=10-5\Big(\cfrac{1}{2}\Big)^{n-1}$

となる。

【考え方2】では，実際に階差数列の形を考えるとよい。

たとえば，$a_2=\cfrac{1}{2}a_1+5$・・・③ である。同様に

$a_3=\cfrac{1}{2}a_2+5$・・・④

となり

④－③

$a_3-a_2=\cfrac{1}{2}(a_2-a_1)$

である。これを $n$ を用いて表すと

$a_{n+2}-a_{n+1}=\cfrac{1}{2}(a_{n+1}-a_n)$

となり，数列 ${a_{n+1}-a_n}$ は公比 $\cfrac{1}{2}$ の階差数列であることが分かる。ここから階差数列の和を用いて一般項を求めてみよう。

階差数列の初項は $a_2-a_1$ で求めることができる。

$a_2=\cfrac{1}{2}a_1+5=\cfrac{1}{2}\times5+5=\cfrac{15}{2}$
$a_2-a_1=\cfrac{15}{2}-5=\cfrac{5}{2}$

よって，階差数列の一般項は $\cfrac{5}{2}\Big(\cfrac{1}{2}\Big)^{n-1}=5\Big(\cfrac{1}{2}\Big)^n$ となる。

階差数列の和を用いて一般項を求めると

$\displaystyle a_n=5+\sum_{k=1}^{n-1} 5\Big(\cfrac{1}{2}\Big)^k$
ここで，$\displaystyle\sum_{k=1}^{n-1}\Big(\cfrac{1}{2}\Big)^k$ は等比数列の和であるから

$a_n=5+5\cdot\cfrac{\cfrac{1}{2}\Big\{{1-\Big(\cfrac{1}{2}\Big)^{n-1}\Big\}}}{1-\cfrac{1}{2}}$
$=5+5\Big\{1-\Big(\cfrac{1}{2}\Big)^{n-1}\Big\}$
$=10-5\Big(\cfrac{1}{2}\Big)^{n-1}$

となり，同様に一般項を求めることができる。

(2)

薬 D については，$M = 2$，$L = 40$ である。薬 D を 12 時間ごとに 1 錠ずつ服用する場合，$n$ 回目の服用直前の血中濃度が $a_n-P$ であることに注意して，正しいものを，次の ⓪ 〜 ⑤ のうちから二つ選べ。 $\boxed{\text{ タ }}$

⓪ 4 回目の服用までは血中濃度が $L$ を超えないが， 5 回目の服用直後に血中濃度が $L$ を超える。

① 5 回目の服用までは血中濃度が $L$ を超えないが，服用し続けるといつか必ず $L$ を超える。

② どれだけ継続して服用しても血中濃度が $L$ を超えることはない。

③ 1 回目の服用直後に血中濃度が $P$ に達して以降，血中濃度が $M$ を下回ることはないので， 1 回目の服用以降は適切な効果が持続する。

④ 2 回目までは服用直前に血中濃度が $M$ 未満になるが， 2 回目の服用以降は，血中濃度が $M$ を下回ることはないので，適切な効果が持続する。

⑤ 5 回目までは服用直前に血中濃度が $M$ 未満になるが， 5 回目の服用以降は，血中濃度が $M$ を下回ることはないので，適切な効果が持続する。

---

正解と解説

$\boxed{\text{ タ }}$ ②，③

$a_n=10-5\Big(\cfrac{1}{2}\Big)^{n-1}$ について考えると，$n$ の値が増加するほど，$\Big(\cfrac{1}{2}\Big)^{n-1}$ は $0$ に近づいていくので，$a_n$ は $10$ に近づいていくことが分かる。よって，血中濃度が $L=40$ を超えることはない。

したがって，⓪，①は不適であり，②は適する。

また，2回目の服用直前の血中濃度は $5\times\cfrac{1}{2}=\cfrac{5}{2}$ となるので $M=2$ を上回る。その後は服薬後の血中濃度は $5$ を上回るため，$ \cfrac{1}{2}$ 倍しても $M=2$ を下回ることはない。したがって，③は適する。④と⑤は，2回目の服薬直前の血中濃度が $M=2$ を上回るので不適。

(3)

(1)と同じ服用量で，服用間隔の条件のみを 24 時間に変えた場合の血中濃度を調べよう。薬 D を 24 時間ごとに 1 錠ずつ服用するときの，$n$ 回目の服用直後の血中濃度を $b_n$ とする。$n$ 回目の服用直前の血中濃度は $b_n-P$ である。最初の服用から $24n$ 時間経過後の服用直前の血中濃度である $a_{2n+1}-P$ と$b_{n+1}-P$ を比較する。$b_{n+1}-P$ と $a_{2n+1}-P$ の比を求めると，$\cfrac{b_{n+1}-P}{a_{2n+1}-P}=\cfrac{\boxed{\text{ チ }}}{\boxed{\text{ ツ }}}$となる。

---

正解と解説

$\boxed{\text{ チ }}, \boxed{\text{ ツ }}$　$1$，$3$

実際に数列 ${b_n}$ を求めるとよい。求め方としては(1)のように特性方程式を用いるか階差数列を用いるが，特性方程式を用いる方が馴染みがあるだろう。文章より，$24$ 時間後の血中濃度は $\cfrac{1}{4}$ になるので

$b_1=5,b_{n+1}=\cfrac{1}{4}b_n+5\cdots$①

$\alpha=\cfrac{1}{4}\alpha+5\cdots$②

①－②

$b_{n+1}-\alpha=\cfrac{1}{4}(b_n-\alpha)$

ここで，②より $\alpha=\cfrac{20}{3}$ となるので

$b_{n+1}-\cfrac{20}{3}=\cfrac{1}{4}\Big(b_n-\cfrac{20}{3}\Big)$

$c_n=b_n-\cfrac{20}{3}$ とおくと

$c_1=b_1-\cfrac{20}{3}=-\cfrac{5}{3}$

$c_n$ は初項 $-\cfrac{5}{3}$，公比 $\cfrac{1}{4}$ の等比数列だから

$c_n=-\cfrac{5}{3}\Big(\cfrac{1}{4}\Big)^{n-1}$
$c_n=-\cfrac{5}{3}\Big(\cfrac{1}{2}\Big)^{2(n-1)}$

よって

$b_n-\cfrac{20}{3}=-\cfrac{5}{3}\Big(\cfrac{1}{2}\Big)^{2(n-1)}$
$b_n=\cfrac{20}{3}-\cfrac{5}{3}\Big(\cfrac{1}{2}\Big)^{2(n-1)}$

これより

$b_{n+1}=\cfrac{20}{3}-\cfrac{5}{3}\Big(\cfrac{1}{2}\Big)^{2n}$

また

$a_{2n+1}=10-5\Big(\cfrac{1}{2}\Big)^{2n}$

$P=5$ より，比を求めると

$\cfrac{b_{n+1}-P}{a_{2n+1}-P}=\cfrac{\cfrac{20}{3}-\cfrac{5}{3}\Big(\cfrac{1}{2}\Big)^{2n}-5}{10-5\Big(\cfrac{1}{2}\Big)^{2n}-5}$
$=\cfrac{\cfrac{5}{3}-\cfrac{5}{3}\Big(\cfrac{1}{2}\Big)^{2n}}{5-5\Big(\cfrac{1}{2}\Big)^{2n}}$
$=\cfrac{1}{3}\Bigg\{\cfrac{5-5\Big(\cfrac{1}{2}\Big)^{2n}}{5-5\Big(\cfrac{1}{2}\Big)^{2n}}\Bigg\}=\cfrac{1}{3}$

(4)

薬 D を 24 時間ごとに $k$ 錠ずつ服用する場合には，最初の服用直後の血中濃度は $kP$ となる。服用量を変化させても $T$ の値は変わらないものとする。薬 D を 12 時間ごとに 1 錠ずつ服用した場合と 24 時間ごとに $k$ 錠ずつ服用した場合の血中濃度を比較すると，最初の服用から $24n$ 時間経過後の各服用直前の血中濃度が等しくなるのは，$k=\boxed{\text{ テ }}$ のときである。したがって， 24 時間ごとに $k$ 錠ずつ服用する場合の各服用直前の血中濃度を，12 時間ごとに 1 錠ずつ服用する場合の血中濃度以上とするためには $k\geqq\boxed{\text{ テ }}$ でなくてはならない。

また，24 時間ごとの服用量を$\boxed{\text{ テ }}$錠にするとき，正しいものを，次の⓪ 〜 ③のうちから一つ選べ。 $\boxed{\text{ ト }}$

⓪ 1 回目の服用以降，服用直後の血中濃度が常に $L$ を超える。

① 4 回目の服用直後までの血中濃度は $L$ 未満だが，5 回目以降は服用直後の血中濃度が常に $L$ を超える。

② 9 回目の服用直後までの血中濃度は $L$ 未満だが，10 回目以降は服用直後の血中濃度が常に $L$ を超える。

③ どれだけ継続して服用しても血中濃度が $L$ を超えることはない。

---

正解と解説

$\boxed{\text{ テ }}，\boxed{\text{ ト }}$ $3$，③

$k$ 錠ずつ服用する場合，血中濃度を表す数列を ${c_n}$ とおくと，${c_n}$ は ${b_n}$ を $k$ 倍したものになる。

$c_n=\cfrac{20}{3}k-\cfrac{5}{3}k\Big(\cfrac{1}{2}\Big)^{2(n-1)}$

これを $ a_{2n+1}=10-5\Big(\cfrac{1}{2}\Big)^{2n}$ と比べる。

(3)を参考にして考えると，服薬直前の血中濃度はそれぞれ $c_{n+1}-5k$，$a_{2n+1}-5$ となるので $c_{n+1}-5k=a_{2n+1}-5$ が成り立つときの $k$ の値を求めればよい。

$c_{n+1}-5k=\cfrac{20}{3}k-\cfrac{5}{3}k\Big(\cfrac{1}{2}\Big)^{2n}-5k$
$=\cfrac{5}{3}k-\cfrac{5}{3}k\Big(\cfrac{1}{2}\Big)^{2n}$
$a_{2n+1}-5=10-5\Big(\cfrac{1}{2}\Big)^{2n}-5$

$=5-5\Big(\cfrac{1}{2}\Big)^{2n}$

これより

$\cfrac{5}{3}k-\cfrac{5}{3}k\Big(\cfrac{1}{2}\Big)^{2n}=5-5\Big(\cfrac{1}{2}\Big)^{2n}$

$k=3$

次に $k=3$ とすると $c_n$ は

$c_n=\cfrac{20}{3}\cdot 3-\cfrac{5}{3}\cdot 3\Big(\cfrac{1}{2}\Big)^{2(n-1)}$
$=20-5\Big(\cfrac{1}{2}\Big)^{2(n-1)}$

式について考えると，$n$ の値が増加するほど，$ \Big(\cfrac{1}{2}\Big)^{2(n-1)}$ は $0$ に近づいていくので，$c_n$ は $20$ に近づいていくことが分かる。よって，血中濃度が $L=40$ を超えることはない。

したがって，選択肢③が正しい。