【スマホで読む・わかりやすい】共通テスト試行H29年度数学IA【解説・正解・問題】
第5問
$n$ を $3$ 以上の整数とする。紙に正方形のマスが縦横とも $(n – 1)$ 個ずつ並んだマス目を書く。その $(n – 1)^2$ 個のマスに,以下のルールに従って数字を一つずつ書き込んだものを「方盤」と呼ぶことにする。なお,横の並びを「行」,縦の並びを「列」という。
ルール: 上から $k$ 行目,左から $\ell$ 列目のマスに,$k$ と $\ell$ の積を $n$ で割った余りを記入する。
$n = 3$,$n = 4$ のとき,方盤はそれぞれ下の図 1 ,図 2 のようになる。
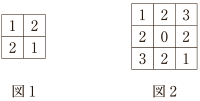
例えば,図 2 において,上から 2 行目,左から 3 列目には,$2 \times 3 = 6$ を $4$ で割った余りである $2$ が書かれている。このとき,次の問いに答えよ。
(1)
$n = 8$ のとき,下の図 3 の方盤の A に当てはまる数を答えよ。$\boxed{\text{ ア }}$
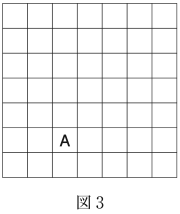
また,図 3 の方盤の上から $5$ 行目に並ぶ数のうち, $1$ が書かれているのは左から何列目であるかを答えよ。左から$\boxed{\text{ イ }}$列目
正解と解説
$\boxed{\text{ ア }}$、$\boxed{\text{ イ }}$ 2、5
Aは上から6行目、左から3列目にあるので
$6\times 3\div 8=2\cdots2$
また、5行目において左から順に余りを求めていくと
$5\times 1\div 8=0\cdots3$
$5\times 2\div 8=1\cdots2$
$5\times 3\div 8=1\cdots7$
$5\times 4\div 8=2\cdots4$
$5\times 5\div 8=3\cdots1$
したがって、左から$5$列目。
(2)
$n = 7$ のとき,下の図 4 のように,方盤のいずれのマスにも 0 が現れない。
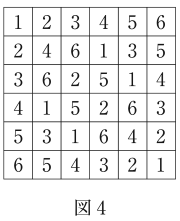
このように,方盤のいずれのマスにも $0$ が現れないための,$n$ に関する必要十分条件を,次の ⓪ 〜 ⑤ のうちから一つ選べ。$\boxed{\text{ ウ }}$
⓪ $n$ が奇数であること。
① $n$ が $4$ で割って $3$ 余る整数であること。
② $n$ が $2$ の倍数でも $5$ の倍数でもない整数であること。
③ $n$ が素数であること。
④ $n$ が素数ではないこと。
⑤ $n – 1$ と $n$ が互いに素であること。
正解と解説
$\boxed{\text{ ウ }}$ ③
$n=1$だと方盤を作ることができないので、$n\geqq 2$となる。また、$k\times\ell$が$n$で割り切れるとき $0$ が現れるので、$n$ で割り切れるかどうかについて考えていけばよい。
⓪ $n$ が奇数の場合
$n=3$ のとき
図1より0が現れることはない。
$n=5$ のとき
$1\times 1\cdots 4\times 4$ の範囲に$5$で割り切れる数はない。つまり、$0$が現れることはない。
$n=7$ のとき
$1\times 1\cdots 6\times 6$ の範囲に$7$で割り切れる数はない。
$n=9$ のとき
$1\times 1\cdots 8\times 8$ の範囲で考えると
$3\times 3=9$ は $9$ で割り切れる。つまり、$0$ が現れる。
よって、⓪は不適。
※この時点で $n$ が素数であれば $n$ で割り切れる数はないことに気づいて、選択肢③を選んでもよいだろう。ここでは念のため、すべての選択肢について検討しておく。
① $n$が$4$で割って$3$余る整数の場合
これに当てはまる数は、$3,7,11,15,\cdots$ である。
$n=3,7$ は⓪で考えたので、$n=11$ から検討する。
$n=11$ のとき
$1\times 1\cdots 10\times 10$ の範囲に$11$で割り切れる数はない。
$n=15$ のとき
$1\times 1\cdots 14\times 14$ の範囲で考えると
$3\times 5=15$ は $15$ で割り切れる
よって、①は不適。
② $n$が$2$の倍数でも$5$の倍数でもない整数の場合
これに当てはまる数は、$3,7,9,11,\cdots$
$n=9$ のとき、不適。
③ $n$が素数の場合
ある素数 $n$ を $n$ より小さい数の積で表すことはできない。したがって、
$1\times 1\cdots (n-1)\times(n-1)$ の範囲に $n$ で割り切れる数はない。
③は適する。
④ $n$が素数ではない場合
$n=9$ のとき、不適。
⑤ $n-1$と$n$が互いに素である場合
$n=9$ のとき、$8$ と $9$ は互いに素であるが、上と同様に不適。
(3) $n$ の値がもっと大きい場合を考えよう。方盤においてどの数字がどのマスにあるかは,整数の性質を用いると簡単に求めることができる。
$n = 56$ のとき,方盤の上から $27$ 行目に並ぶ数のうち, $1$ は左から何列目にあるかを考えよう。
(3)(i)
方盤の上から $27$ 行目,左から $\ell$ 列目の数が $1$ であるとする(ただし,$1\leqq \ell \leqq 55)$。$\ell$ を求めるためにはどのようにすれば良いか。正しいものを,次の ⓪ 〜 ③ のうちから一つ選べ。 $\boxed{\text{ エ }}$
⓪ $1$ 次不定方程式 $27\ell – 56m = 1$ の整数解のうち,$1 \leqq \ell \leqq 55$ を満たすものを求める。
① $1$ 次不定方程式 $27\ell – 56m = -1$ の整数解のうち,$1 \leqq \ell \leqq 55$ を満たすものを求める。
② $1$ 次不定方程式 $56\ell – 27m = 1$ の整数解のうち,$1 \leqq \ell \leqq 55$ を満たすものを求める。
③ $1$ 次不定方程式 $56\ell – 27m = -1$ の整数解のうち,$1 \leqq \ell \leqq 55$ を満たすものを求める。
正解と解説
$\boxed{\text{ エ }}$ ⓪
商を $m$ として、$27\times\ell\div 56=m\dots1$ となる場合を考える。
式を変形して
$27\ell=56m+1$
$27\ell-56m=1$
(3)(ii)
(i)で選んだ方法により,方盤の上から $27$ 行目に並ぶ数のうち, $1$ は左から何列目にあるかを求めよ。左から $\boxed{\text{ オカ }}$列目
正解と解説
$\boxed{\text{ オカ }}$ 27
$27\ell-56m=1$ について、
互除法を用いて $1\leqq\ell\leqq 55$ の範囲であてはまる $\ell$ の値を求める。
$56=27\cdot 2+2$
$27=2\cdot 13+1$
それぞれ移項して
$2=56-27\cdot 2$
$1=27-2\cdot 13$
ここから
$1=27-(56-27\cdot 2)\cdot 13$
$1=27-56\cdot 13+27\cdot 2\cdot 13$
$1=27\cdot 27-56\cdot 13$
したがって$\ell=27$
(4) $n = 56$ のとき,方盤の各行にそれぞれ何個の $0$ があるか考えよう。
(4)(i)
方盤の上から $24$ 行目には $0$ が何個あるか考える。
左から $\ell$ 列目が $0$ であるための必要十分条件は,$24\ell$ が $56$ の倍数であること,すなわち,$\ell$ が $\boxed{\text{ キ }}$ の倍数であることである。したがって, 上から $24$ 行目には $0$ が $\boxed{\text{ ク }}$ 個ある。
正解と解説
$\boxed{\text{ キ }}$、$\boxed{\text{ ク }}$ $7$、$7$
$56$ の倍数を $56s$ とすると
$24\ell=56s$
$3\ell=7s$
$3$ と $7$ は互いに素だから、$\ell$ は $7$ の倍数である。
また、$1\leqq\ell\leqq55$ の範囲に $7$ の倍数は $7$ 個ある。
(4)(ii)
上から 1 行目から 55 行目までのうち, 0 の個数が最も多いのは上から何行目であるか答えよ。上から $\boxed{\text{ ケコ }}$ 行目
正解と解説
$\boxed{\text{ ケコ }}$ $28$
(i)から推測する。$1\leqq\ell\leqq55$ の範囲で倍数がもっとも多くなる場合を考えると、$\ell$が$2$の倍数のときである。上から$k$行目において、$\ell=2t$とおくと
$k\cdot 2t=56s$
$kt=28s$
このとき、$k=28$ とすると $kt$ は $t$ の値に関係なく $28$ で割り切れる。
(5)
$n = 56$ のときの方盤について,正しいものを,次の ⓪ 〜 ⑤ のうちからすべて選べ。 $\boxed{\text{ サ }}$
⓪ 上から $5$ 行目には $0$ がある。
① 上から $6$ 行目には $0$ がある。
② 上から $9$ 行目には $1$ がある。
③ 上から $10$ 行目には $1$ がある。
④ 上から $15$ 行目には $7$ がある。
⑤ 上から $21$ 行目には $7$ がある。
正解と解説
$\boxed{\text{ サ }}$ ①、②、④
$1\leqq\ell\leqq55$ に注意して、
⓪
$5\ell=56s$ とおくと
$5$と$56$は互いに素だから、$\ell$は$56$の倍数となる。よって、不適。
①
$6\ell=56s$ とおくと
$3\ell=28s$
$3$と$28$は互いに素だから、$\ell$は$28$の倍数となる。したがって、$\ell=28$ のとき$0$となる。
②
$9\ell-56m=1$ とおくと
互除法を用いて
$56=9\cdot 6+2$
$9=2\cdot 4+1$
それぞれ移項して
$2=56-9\cdot 6$
$1=9-2\cdot 4$
これより
$1=9-(56-9\cdot 6)\cdot 4$
$1=9-56\cdot 4+9\cdot24$
$1=9\cdot 25-56\cdot 4$
したがって、$\ell=25$ のとき$1$となる。
③
$10\ell-56m=1$ とおくと
互除法を用いて
$56=10\cdot5+6$
$10=6\cdot 1+4$
$6=4\cdot 1+2$
$4=2\cdot 2$
したがって、$10\ell-56m=1$ となる$\ell,m$は存在しない。
※これは、$10$の倍数と$56$の倍数がともに偶数であることから、その差が$1$になることはないと考えてもよい。
④
$15\ell-56m=7$ から
$15\ell-56m=1$ とおくと
互除法を用いて
$56=15\cdot 3+11$
$15=11\cdot 1+4$
$11=4\cdot 2+3$
$4=3\cdot 1+1$
それぞれ移項して
$11=56-15\cdot 3$
$4=15-11$
$3=11-4\cdot 2$
$1=4-3$
これより
$1=4-(11-4\cdot2)$
$=4\cdot3-11$
$=(15-11)\cdot3-11$
$=15\cdot3-11\cdot4$
$=15\cdot3-(56-15\cdot3)\cdot4$
$=15\cdot15-56\cdot4$
両辺を$7$倍して
$15\cdot105-56\cdot27=7\cdots$①
$15\ell-56m=7\cdots$②
②-①
$15(\ell-105)-56(m-27)=0$
$15(\ell-105)=56(m-27)$
$15$と$56$は互いに素だから、
$\ell-105$は$56$の倍数
$\ell-105=56u$とおくと
$\ell=56u+105$
ここで$u=-1$とすると、$\ell=-56+105=49$となり$1\leqq\ell\leqq55$を満たす$\ell$が存在する。よって、適する。
⑤
$21\ell-56m=7$ とおくと
$3\ell-8m=1\cdots$①
恒等式が成り立つ$\ell$と$m$を考えると
$3(-5)-8(-2)=1\cdots$②
①-②
$3(\ell+5)-8(m+2)=0$
$3(\ell+5)=8(m+2)$
$3$と$8$は互いに素だから、$\ell+5$は$8$の倍数である。
$\ell+5=8u$ とおくと
$\ell=8u-5$
$u=1$のとき$\ell=3$となり、$1\leqq\ell\leqq55$を満たす$\ell$が存在する。よって、適する。
SNSでシェア