【スマホで読む・わかりやすい】共通テスト試行H29年度数学IA【解説・正解・問題】
第4問
花子さんと太郎さんは,正四面体 ABCD の各辺の中点を次の図のように E,F,G,H,I,J としたときに成り立つ性質について,コンピュータソフトを使いながら,下のように話している。二人の会話を読んで,下の問いに答えよ。
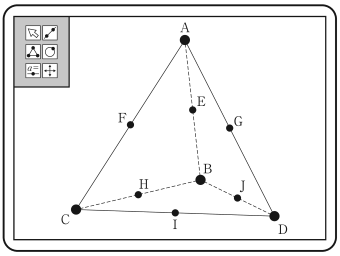
花子:四角形 FHJG は平行四辺形に見えるけれど,正方形ではないかな。
太郎: 4 辺の長さが等しいことは,簡単に証明できそうだよ。
(1) 太郎さんは四角形 FHJG の 4 辺の長さが等しいことを,次のように証明した。
太郎さんの証明
$\boxed{\text{ ア }}$ により,四角形 FHJG の各辺の長さはいずれも正四面体 ABCD の 1 辺の長さの $\boxed{\text{ イ }}$ 倍であるから, 4 辺の長さが等しくなる。
(1)(i)
$\boxed{\text{ ア }}$ に当てはまる最も適当なものを,次の ⓪ 〜 ④ のうちから一つ選べ。
⓪ 中線定理 ① 方べきの定理 ② 三平方の定理
③ 中点連結定理 ④ 円周角の定理
正解
$\boxed{\text{ ア }}$ ③
(1)(ii)
$\boxed{\text{ イ }}$ に当てはまるものを,次の ⓪ 〜 ④ のうちから一つ選べ。
⓪ 2 ① $\displaystyle\frac{3}{4}$ ② $\displaystyle\frac{2}{3}$ ③ $\displaystyle\frac{1}{2}$ ④ $\displaystyle\frac{1}{3}$
正解
$\boxed{\text{ イ }}$ ③
(2) 花子さんは,太郎さんの考えをもとに,正四面体をいろいろな方向から見て,四角形 FHJG が正方形であることの証明について,下のような構想をもとに,実際に証明した。
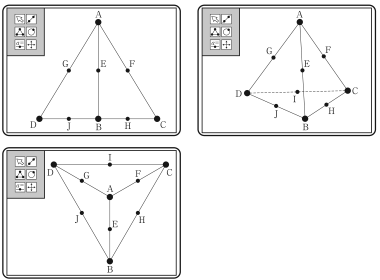
花子さんの構想
四角形において, 4 辺の長さが等しいことは正方形であるための $\boxed{\text{ ウ }}$。さらに,対角線 FJ と GH の長さが等しいことがいえれば,四角形 FHJG が正方形であることの証明となるので,△FJC と △GHD が合同であることを示したい。
しかし,この二つの三角形が合同であることの証明は難しいので,別の三角形の組に着目する。
花子さんの証明
点 F,点 G はそれぞれ AC,AD の中点なので,二つの三角形 $\boxed{\text{ エ }}$ と $\boxed{\text{ オ }}$ に着目する。$\boxed{\text{ エ }}$ と $\boxed{\text{ オ }}$ は 3 辺の長さがそれぞれ等しいので合同である。このとき,$\boxed{\text{ エ }}$ と $\boxed{\text{ オ }}$ は $\boxed{\text{ カ }}$ で,F と G はそれぞれ AC,AD の中点なので,FJ = GH である。
よって,四角形 FHJG は, 4 辺の長さが等しく対角線の長さが等しいので正方形である。
(2)(i)
$\boxed{\text{ ウ }}$ に当てはまるものを,次の ⓪ 〜 ③ のうちから一つ選べ。
⓪ 必要条件であるが十分条件でない
① 十分条件であるが必要条件でない
② 必要十分条件である
③ 必要条件でも十分条件でもない
正解と解説
$\boxed{\text{ ウ }}$ ⓪
四角形において、4辺の長さが等しくても正方形になるとは限らないが、正方形であれば4辺の長さは等しい。したがって、4辺の長さが等しいことは正方形であるための必要条件であるが十分条件でない。
(2)(ii)
$\boxed{\text{ エ }}$,$\boxed{\text{ オ }}$ に当てはまるものが,次の ⓪ 〜 ⑤ の中にある。当てはまるものを一つずつ選べ。ただし,$\boxed{\text{ エ }}$ と $\boxed{\text{ オ }}$ の解答の順序は問わない。
⓪ △AGH ① △AIB ② △AJC
③ △AHD ④ △AHC ⑤ △AJD
正解と解説
$\boxed{\text{ エ }}$,$\boxed{\text{ オ }}$ ②、③
ここでは、FJ=GHを示したいので、FJとGHをそれぞれ面の一部として含んでいる三角形を選ぶとよい。
(2)(iii)
$\boxed{\text{ カ }}$ に当てはまるものを,次の ⓪ 〜 ③ のうちから一つ選べ。
⓪ 正三角形 ① 二等辺三角形
② 直角三角形 ③ 直角二等辺三角形
正解と解説
$\boxed{\text{ カ }}$ ①
△AJCはAJ=CJの二等辺三角形であり、同様に△AHDはAH=DHの二等辺三角形である。
四角形 FHJG が正方形であることを証明した太郎さんと花子さんは,さらに,正四面体 ABCD において成り立つ他の性質を見いだし,下のように話している。
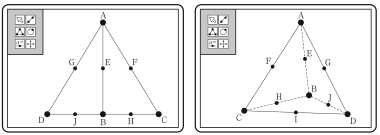
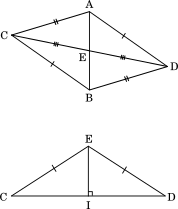
花子:線分 EI と辺 CD は垂直に交わるね。
太郎:そう見えるだけかもしれないよ。証明できる?
花子: (a)辺 CD は線分 AI とも BI とも垂直だから,(b)線分 EI と辺 CD は垂直といえるよ。
太郎: そうか……。ということは,(c)この性質は,四面体 ABCD が正四面体でなくても成り立つ場合がありそうだね。
(3)
下線部(a)から下線部(b)を導く過程で用いる性質として正しいものを,次の⓪ 〜 ④ のうちからすべて選べ。 $\boxed{\text{ キ }}$
⓪ 平面 $a$ 上にある直線 $\ell$ と平面 $a$ 上にない直線 $m$ が平行ならば,$a // m$ である。
① 平面 $a$ 上にある直線 $\ell$,$m$ が点 P で交わっているとき,点 P を通り平面 $a$ 上にない直線 $n$ が直線 $\ell$,$m$ に垂直ならば,$a$ ⊥ $n$ である。
② 平面 $a$ と直線 $\ell$ が点 P で交わっているとき,$a$ ⊥ $\ell$ ならば,平面 $a$ 上の点 P を通るすべての直線 $m$ に対して,$\ell$ ⊥ $m$ である。
③ 平面 $a$ 上にある直線 $\ell$,$m$ がともに平面 $a$ 上にない直線 $n$ に垂直ならば,$a$ ⊥ $n$ である。
④ 平面 $a$ 上に直線 $\ell$,平面 $\beta$ 上に直線 $m$ があるとき,$a$ ⊥ $\beta$ ならば,$\ell$ ⊥ $m$ である。
正解と解説
$\boxed{\text{ キ }}$ ①、②
①を正四面体ABCDに当てはめると、△AIBを含む平面を$\alpha$として
平面$\alpha$上にある直線AI、BIが点Iで交わっているとき、点Iを通り平面$\alpha$上にない直線CDが直線AI、BIに垂直ならば、$\alpha$⊥CD である。
②を当てはめると、△AIBを含む平面を$\alpha$として
平面$\alpha$と直線CDが点Iで交わっているとき、$\alpha$⊥CDならば、平面$\alpha$上の点Iを通るすべての直線$m$に対して、CD⊥$m$である。したがって、CD⊥AI、CD⊥BIが成り立つ。
(4)
下線部(c)について,太郎さんと花子さんは正四面体でない場合についても考えてみることにした。
四面体 ABCD において,AB,CD の中点をそれぞれ E,I とするとき,下線部(b)が常に成り立つ条件について,次のように考えた。
太郎さんが考えた条件: AC = AD,BC = BD
花子さんが考えた条件: BC = AD,AC = BD
四面体 ABCD において,下線部(b)が成り立つ条件について正しく述べているものを,次の ⓪ 〜 ③ のうちから一つ選べ。 $\boxed{\text{ ク }}$
⓪ 太郎さんが考えた条件,花子さんが考えた条件のどちらにおいても常に成り立つ。
① 太郎さんが考えた条件では常に成り立つが,花子さんが考えた条件では必ずしも成り立つとは限らない。
② 太郎さんが考えた条件では必ずしも成り立つとは限らないが,花子さんが考えた条件では常に成り立つ。
③ 太郎さんが考えた条件,花子さんが考えた条件のどちらにおいても必ずしも成り立つとは限らない。
正解と解説
$\boxed{\text{ ク }}$ ①
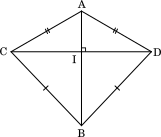
展開図を描いて検討するとよい。
(i) AC=AD、BD=BDのとき
△ACDと△BCDはともに二等辺三角形である。
よって、AB⊥CD
したがって、EI⊥CD
(ii) BC=AD、AC=BDのとき
四角形ABCDは平行四辺形となるので、
EC=ED
△ECDは二等辺三角形となるので
EI⊥CD
SNSでシェア