【スマホで読む・わかりやすい】共通テスト試行H29年度数学IA【解説・正解・問題】
第3問
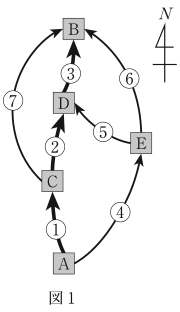
高速道路には,渋滞状況が表示されていることがある。目的地に行く経路が複数ある場合は,渋滞中を示す表示を見て経路を決める運転手も少なくない。太郎さんと花子さんは渋滞中の表示と車の流れについて,仮定をおいて考えてみることにした。
A 地点(入口)から B 地点(出口)に向かって北上する高速道路には,図 1 のように分岐点 A,C,E と合流点 B,D がある。①,②,③は主要道路であり,④,⑤,⑥,⑦7は迂回道路である。ただし,矢印は車の進行方向を表し,図 1 の経路以外に A 地点から B 地点に向かう経路はないとする。また,各分岐点 A,C,E には,それぞれ①と④,②と⑦,⑤と⑥の渋滞状況が表示される。
太郎さんと花子さんは,まず渋滞中の表示がないときに,A,C,E の各分岐点において運転手がどのような選択をしているか調査した。その結果が表 1 である。
これに対して太郎さんは,運転手の選択について,次のような仮定をおいて確率を使って考えることにした。
太郎さんの仮定
(i) 表 1 の選択の割合を確率とみなす。
(ii) 分岐点において,二つの道路のいずれにも渋滞中の表示がない場合,またはいずれにも渋滞中の表示がある場合,運転手が道路を選択する確率は(i)でみなした確率とする。
(iii) 分岐点において,片方の道路にのみ渋滞中の表示がある場合,運転手が渋滞中の表示のある道路を選択する確率は(i)でみなした確率の$\displaystyle\frac{2}{3}$倍とする。
ここで,(i)の選択の割合を確率とみなすとは,例えば A 地点の分岐において④の道路を選択した割合 $\displaystyle\frac{91}{1183}=\frac{1}{13}$ を④の道路を選択する確率とみなすということである。
太郎さんの仮定のもとで,次の問いに答えよ。
(1)
すべての道路に渋滞中の表示がない場合,A 地点の分岐において運転手が①の道路を選択する確率を求めよ。$\displaystyle\frac{\boxed{\text{ アイ }}}{\boxed{\text{ ウエ }}}$
正解と解説
$\displaystyle\frac{\boxed{\text{ アイ }}}{\boxed{\text{ ウエ }}}$ 12、13
$\displaystyle\frac{1092}{1183}=\frac{12}{13}$
(2)
すべての道路に渋滞中の表示がない場合,A 地点から B 地点に向かう車が D 地点を通過する確率を求めよ。$\displaystyle\frac{\boxed{\text{ オカ }}}{\boxed{\text{ キク }}}$
正解と解説
$\displaystyle\frac{\boxed{\text{ オカ }}}{\boxed{\text{ キク }}}$ 11、13
いったん、それぞれの道路について通過する確率を求めると
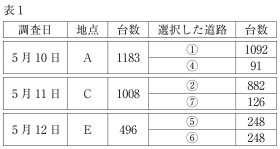
① $\displaystyle\frac{12}{13}$ ④ $\displaystyle\frac{1}{13}$
② $\displaystyle\frac{882}{1008}=\frac{7}{8}$ ⑦ $\displaystyle\frac{1}{8}$
⑤ $\displaystyle\frac{248}{496}=\frac{1}{2}$ ⑥ $\displaystyle\frac{1}{2}$
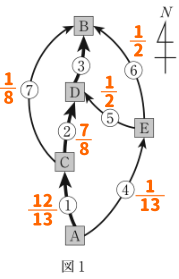
したがって、D地点を通過する確率は
$\displaystyle\frac{12}{13}\times\frac{7}{8}+\frac{1}{13}\times{1}{2}=\frac{11}{13}$
(3)
すべての道路に渋滞中の表示がない場合,A 地点から B 地点に向かう車で D 地点を通過した車が,E 地点を通過していた確率を求めよ。$\displaystyle\frac{\boxed{\text{ ケ }}}{\boxed{\text{ コサ }}}$
正解と解説
$\displaystyle\frac{\boxed{\text{ ケ }}}{\boxed{\text{ コサ }}}$ 1、22
D地点を通過した車が、E地点を通過する条件付き確率を求めると
$\displaystyle\frac{\frac{1}{26}}{\frac{11}{13}}=\frac{1}{22}$
(4)
①の道路にのみ渋滞中の表示がある場合,A 地点から B 地点に向かう車 D 地点を通過する確率を求めよ。$\displaystyle\frac{\boxed{\text{ シス }}}{\boxed{\text{ セソ }}}$
正解と解説
$\displaystyle\frac{\boxed{\text{ シス }}}{\boxed{\text{ セソ }}}$ 19、26
渋滞中の表示がある場合、通過する台数は$\displaystyle\frac{2}{3}$倍となるので
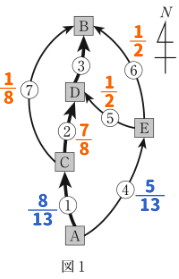
①を通過する確率は $\displaystyle\frac{12}{13}\times\frac{2}{3}=\frac{8}{13}$
④を通過する確率は $\displaystyle 1-\frac{8}{13}=\frac{5}{13}$
となる。
したがって、D地点を通過する確率は
$\displaystyle\frac{8}{13}\times\frac{7}{8}+\frac{5}{13}\times\frac{1}{2}=\frac{19}{26}$
各道路を通過する車の台数が 1000 台を超えると車の流れが急激に悪くなる。 一方で各道路の通過台数が 1000 台を超えない限り,主要道路である①,②,③ をより多くの車が通過することが社会の効率化に繋がる。したがって,各道路の
通過台数が 1000 台を超えない範囲で,①,②,③をそれぞれ通過する台数の合計が最大になるようにしたい。
このことを踏まえて,花子さんは,太郎さんの仮定を参考にしながら,次のような仮定をおいて考えることにした。
花子さんの仮定
(i) 分岐点において,二つの道路のいずれにも渋滞中の表示がない場合,またはいずれにも渋滞中の表示がある場合,それぞれの道路に進む車の割合は表 1 の割合とする。
(ii) 分岐点において,片方の道路にのみ渋滞中の表示がある場合,渋滞中の表示のある道路に進む車の台数の割合は表 1 の割合の $\displaystyle\frac{2}{3}$ 倍とする。
過去のデータから 5 月 13 日に A 地点から B 地点に向かう車は 1560 台と想定している。そこで,花子さんの仮定のもとでこの台数を想定してシミュレーションを行った。このとき,次の問いに答えよ。
(5)
すべての道路に渋滞中の表示がない場合,①を通過する台数は $\boxed{\text{ タチツテ }}$ 台となる。よって,①の通過台数を 1000 台以下にするには,①に渋滞中の表示を出す必要がある。
①に渋滞中の表示を出した場合,①の通過台数は $\boxed{\text{ トナニ }}$ 台となる。
正解と解説
$\boxed{\text{ タチツテ }}$、$\boxed{\text{ トナニ }}$ 1440、960
渋滞中の表示がない場合、①を通過する台数は $\displaystyle 1560\times\frac{12}{13}=1440$台
渋滞中の表示がある場合は $\displaystyle 1440\times\frac{2}{3}=960$台
(6)
各道路の通過台数が 1000 台を超えない範囲で,①,②,③をそれぞれ通過する台数の合計を最大にするには,渋滞中の表示を $\boxed{\text{ ヌ }}$ のようにすればよい。$\boxed{\text{ ヌ }}$ に当てはまるものを,次の ⓪ 〜 ③ のうちから一つ選べ。
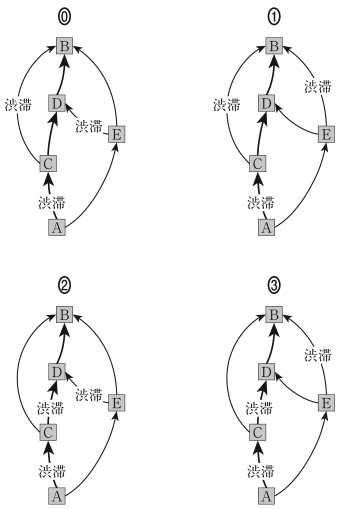
正解と解説
$\boxed{\text{ ヌ }}$ ③
まず、通過台数が1000台を超えないようにするため、①に渋滞中の表示をしなければならない。このとき、通過台数は(5)より$960$台である。
次に、②になるべく多くの車を通過させるために⑦に渋滞中の表示をすることを考える。
この場合、⑦を通過する台数は $\displaystyle\frac{1}{8}\times{2}{3}=\frac{1}{12}$
②を通過する確率は $\displaystyle 1-\frac{1}{12}=\frac{11}{12}$
よって、②を通過する台数は $\displaystyle 960\times\frac{11}{12}=880$台
D地点を通過する車は880台だから、⑤を通過する車は120台以下でなければならない。
④を通過する台数は $1560-960=600$台
⑤に渋滞中の表示した場合に⑤を通過する確率を求めると
$\displaystyle \frac{1}{2}\times\frac{2}{3}=\frac{1}{3}$
⑤を通過する台数は $\displaystyle 600\times\frac{1}{2}=200$台 となり、不適。
今度は、②に渋滞中の表示をする。
②を通過する確率は $\displaystyle\frac{7}{8}\times\frac{2}{3}=\frac{7}{12}$
②を通過する台数は $\displaystyle 960\times\frac{7}{12}=560$台
⑤を通過する車は440台以下でなければならない。
④を通過する台数は$600$台であり、
⑤に渋滞中の表示をする場合
⑤を通過する確率は $\displaystyle\frac{1}{2}\times\frac{2}{3}=\frac{1}{3}$
⑤を通過する台数は $\displaystyle 600\times\frac{1}{3}=200$台
⑥に渋滞中の表示をする場合
⑥を通過する確率は $\displaystyle\frac{1}{2}\times\frac{2}{3}=\frac{1}{3}$
⑤を通過する確率は $\displaystyle 1-\frac{1}{3}=\frac{2}{3}$
⑤を通過する台数は $\displaystyle 600\times\frac{2}{3}=400$台
D地点を通過する台数をなるべく1000台に近くしたいので
⑥に渋滞中の表示をするとよい。
したがって、選択肢③が適する。
SNSでシェア