【スマホで読む・わかりやすい】共通テスト試行H29年度数学IA【解説・正解・問題】
第2問
〔 1 〕 ◯◯高校の生徒会では,文化祭でTシャツを販売し,その利益をボランティア団体に寄付する企画を考えている。 生徒会執行部では,できるだけ利益が多くなる価格を決定するために,次のような手順で考えることにした。
価格決定の手順
(i) アンケート調査の実施
200 人の生徒に,「Tシャツ 1 枚の価格がいくらまでであればTシャツを購入してもよいと思うか」について尋ね,500 円,1000 円, 1500 円,2000 円の四つの金額から一つを選んでもらう。
(ii) 業者の選定
無地のTシャツ代とプリント代を合わせた「製作費用」が最も安い業者を選ぶ。
(iii) Tシャツ 1 枚の価格の決定
価格は「製作費用」と「見込まれる販売数」をもとに決めるが,販売時に釣り銭の処理で手間取らないよう 50 の倍数の金額とする。
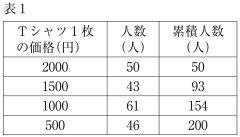
下の表 1 は,アンケート調査の結果である。生徒会執行部では,例えば, 価格が 1000 円のときには 1500 円や 2000 円と回答した生徒も 1 枚購入すると考えて,それぞれの価格に対し,その価格以上の金額を回答した生徒の人数を「累積人数」として表示した。
このとき,次の問いに答えよ。
〔1〕(1)
売上額は
(売上額)=(Tシャツ 1 枚の価格)$\times$(販売数)
と表せるので,生徒会執行部では,アンケートに回答した 200 人の生徒について,調査結果をもとに,表 1 にない価格の場合についても販売数を予測することにした。そのために,Tシャツ 1 枚の価格を $x$ 円,このときの販売数を $y$ 枚とし,$x$ と $y$ の関係を調べることにした。
表 1 のTシャツ 1 枚の価格と $\boxed{\text{ ア }}$ の値の組を$(x,y)$として座標平面上に表すと,その 4 点が直線に沿って分布しているように見えたので,この直線を,Tシャツ 1 枚の価格 $x$ と販売数 $y$ の関係を表すグラフとみなすことにした。
このとき,$y$ は $x$ の $\boxed{\text{ イ }}$ であるので,売上額を $S(x)$ とおくと, $S(x)$ は $x$ の $\boxed{\text{ ウ }}$ である。このように考えると,表 1 にない価格の場合についても売上額を予測することができる。
$\boxed{\text{ ア }}$,$\boxed{\text{ イ }}$,$\boxed{\text{ ウ }}$に入るものとして最も適当なものを,次の ⓪ 〜 ⑥ のうちから一つずつ選べ。ただし,同じものを繰り返し選んでもよい。
⓪ 人数 ① 累積人数 ② 製作費用 ③ 比例
④ 反比例 ⑤ 1 次関数 ⑥ 2 次関数
正解と解説
$\boxed{\text{ ア }}$,$\boxed{\text{ イ }}$,$\boxed{\text{ ウ }}$ ①、⑤、⑥
$y$ は販売数であるが、表1の累積人数が見込まれる販売数となる。また、$x$ と $y$ の関係が直線で表されるとき、$y$ は $x$ の一次関数である。このとき $y=ax+b$ とおくと、売上高はTシャツ1枚の価格×累積人数となるので、
$S(x)=x(ax+b)=ax^2+bx$
したがって、$S(x)$ は $x$ の二次関数である。
生徒会執行部が(1)で考えた直線は,表 1 を用いて座標平面上にとった 4 点のうち $x$ の値が最小の点と最大の点を通る直線である。この直線を用いて,次の問いに答えよ。
〔1〕(2)
売上額 $S(x)$ が最大になる $x$ の値を求めよ。 $\boxed{\text{ エオカキ }}$
正解と解説
$\boxed{\text{ エオカキ }}$ $1250$
$x$ の値が最小と最大の点はそれぞれ $(500,200),(2000,50)$ である。ここから直線の式を求めると、 $y=ax+b$ にそれぞれ代入して
$200=500a+b\cdots$①
$50=2000a+b\cdots$②
①-②
$150=-1500a$
$\displaystyle a=-\frac{1}{10}$
①に代入して
$\displaystyle 200=500\left(-\frac{1}{10}\right)+b$
$b=250$
したがって $\displaystyle y=-\frac{1}{10}x+250$
これより $S(x)$ は
$\displaystyle S(x)=x\left(-\frac{1}{10}x+250\right)$
$\displaystyle =-\frac{1}{10}x^2+250x$
平方完成すると
$\displaystyle S(x)=-\frac{1}{10}\left(x-1250\right)^2+156250$
※解答を導く上で $156250$ の値は不要である。従って $S(x)=-\frac{1}{10}\left(x-1250\right)^2+k$ などとして、計算を省略するとよいだろう。
したがって $S(x)$ は上に凸のグラフとなるので、$x=1250$ のときに最大値をとる。
〔1〕(3)
Tシャツ 1 枚当たりの「製作費用」が 400 円の業者に 120 枚を依頼することにしたとき,利益が最大になるTシャツ 1 枚の価格を求めよ。
$\boxed{\text{ クケコサ }}$ 円
正解と解説
$\boxed{\text{ クケコサ }}$ 1300
まず売上高 $S(x)$ のグラフが示すことを考えるとよい。Tシャツ1枚の価格が$1250$円を下回ると、販売数は増えるもののTシャツ1枚の価格が低いため全体としての売上高は減少する。また、$1250$円を上回ると、販売数が減少し全体としての売上高は減少する。
$x=1250$ のときの販売数は $\displaystyle-\frac{1}{10}\times 1250+250=125$ であるが、問題文より最大で$120$枚しか販売できないので、実際の売上高は$1250\times120=150,000$円となる。
さらに、Tシャツ1枚の価格が$1250$円を下回ると、価格に比例して売上高も減少する。
次に、問題文よりTシャツ1枚の価格が50円刻みであることに注意して、$x=1300$ のときの販売数は $\displaystyle-\frac{1}{10}\times 1300+250=120$ であり、販売高は $1300\times120=156,000$円となる。
さらに、Tシャツ1枚の価格が$1300$円より高くなると、$S(x)$ より売上高は減少する。
これをグラフで表すと次のようになる。

したがって、$1300$円のとき利益は最大となる。
※正しくは売上高から仕入れの金額を引いたものが利益となるが、ここでは考慮しなくてもよい。
〔 2 〕 地方の経済活性化のため,太郎さんと花子さんは観光客の消費に着目し,その拡大に向けて基礎的な情報を整理することにした。以下は,都道府県別の統計データを集め,分析しているときの二人の会話である。会話を読んで下の問いに答えよ。ただし,東京都,大阪府,福井県の 3 都府県のデータは含まれていない。また,以後の問題文では「道府県」を単に「県」として表記する。
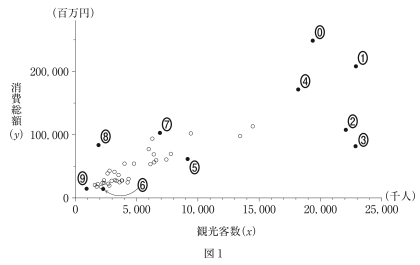
太郎: 各県を訪れた観光客数を $x$ 軸,消費総額を $y$ 軸にとり,散布図をつくると図 1 のようになったよ。
花子: 消費総額を観光客数で割った消費額単価が最も高いのはどこかな。
太郎: 元のデータを使って県ごとに割り算をすれば分かるよ。北海道は……。44 回も計算するのは大変だし,間違えそうだな。
花子:図 1 を使えばすぐ分かるよ。
〔2〕(1)
図 1 の観光客数と消費総額の間の相関係数に最も近い値を,次の ⓪ 〜 ④ のうちから一つ選べ。 $\boxed{\text{ シ }}$
⓪ $-0.85$ ① $-0.52$ ② $0.02$ ③ $0.34$ ④ $0.83$
正解と解説
$\boxed{\text{ シ }}$ ④
図1から観光客数と消費総額の間に強い正の相関があると言えるので、0.83を選ぶ。
〔2〕(2)
44 県それぞれの消費額単価を計算しなくても,図 1 の散布図から消費額単価が最も高い県を表す点を特定することができる。その方法を,「直線」という単語を用いて説明せよ。解答は,解答欄$\boxed{\text{ (う) }}$に記述せよ。
正解と解説
$\boxed{\text{ (う) }}$ 各県を表す点のうち、その点と原点を通る直線の傾きが最も大きい点を選ぶ。
直線の傾きは$\displaystyle\frac{y\text{の変化量}}{x\text{の変化量}}$で求められる。消費額単価が高くなると、$x$の変化量$1$に対する$y$の値が大きくなるので、傾きが大きくなる。
〔2〕(3)
消費額単価が最も高い県を表す点を,図 1 の ⓪ 〜 ⑨ のうちから一つ選べ。$\boxed{\text{ ス }}$
正解と解説
$\boxed{\text{ ス }}$ ⑧
(2)より、原点と結んだ直線の傾きが最も大きくなるものを選べばよい。
花子: 元のデータを見ると消費額単価が最も高いのは沖縄県だね。沖縄県の消費額単価が高いのは,県外からの観光客数の影響かな。
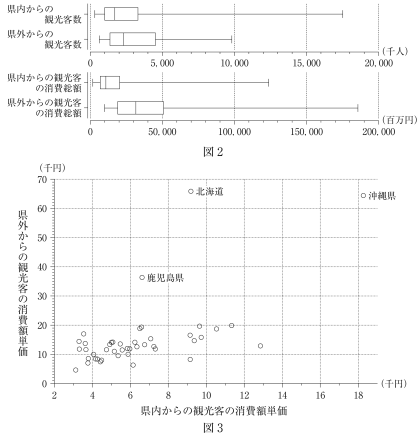
太郎: 県内からの観光客と県外からの観光客とに分けて 44 県の観光客数と消費総額を箱ひげ図で表すと図 2 のようになったよ。
花子: 私は県内と県外からの観光客の消費額単価をそれぞれ横軸と縦軸にとって図 3 の散布図をつくってみたよ。沖縄県は県内,県外ともに観光客の消費額単価は高いね。それに,北海道,鹿児島県,沖縄県は全体の傾向から外れているみたい。
〔2〕(4)
図 2 ,図 3 から読み取れる事柄として正しいものを,次の ⓪ 〜 ④ のうちから二つ選べ。 $\boxed{\text{ セ }}$
⓪ 44 県の半分の県では,県内からの観光客数よりも県外からの観光客数の方が多い。
① 44 県の半分の県では,県内からの観光客の消費総額よりも県外からの観光客の消費総額の方が高い。
② 44 県の 4 分の 3 以上の県では,県外からの観光客の消費額単価の方が県内からの観光客の消費額単価より高い。
③ 県外からの観光客の消費額単価の平均値は,北海道,鹿児島県,沖縄県を除いた 41 県の平均値の方が 44 県の平均値より小さい。
④ 北海道,鹿児島県,沖縄県を除いて考えると,県内からの観光客の消費額単価の分散よりも県外からの観光客の消費額単価の分散の方が小さい。
正解と解説
$\boxed{\text{ セ }}$ ②、③
図2から、ある県における県内からの観光客数と県外からの観光客数を比べることはできない。同様に、観光客の消費総額も比べることもできない。したがって、①、②は不適。
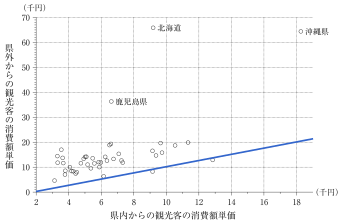
上の図のように直線を引く。直線上の県では県内と県外の単価が一致し、直線の上側にある県は県外の単価が高い。したがって、②は適する。
また、北海道、鹿児島県、沖縄県はその他に比べて県外の単価が著しく高いので、これら3つを加えた44県の平均は、加えない41県の平均を上回る。したがって、③は適する。
さらに、分散については、図から読み取ることは困難である。したがって、④は不適。
〔2〕(5)
二人は県外からの観光客に焦点を絞って考えることにした。
花子: 県外からの観光客数を増やすには,イベントなどを増やしたらいいんじゃないかな。
太郎: 44 県の行祭事・イベントの開催数と県外からの観光客数を散布図にすると,図 4 のようになったよ。
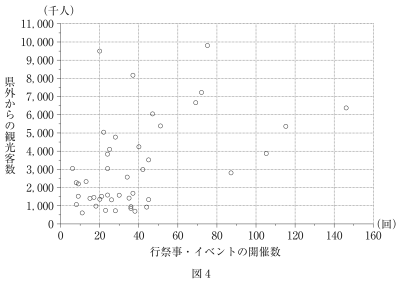
図 4 から読み取れることとして最も適切な記述を,次の ⓪ 〜 ④ のうちから一つ選べ。 $\boxed{\text{ ソ }}$
⓪ 44 県の行祭事・イベント開催数の中央値は,その平均値よりも大きい。
① 行祭事・イベントを多く開催し過ぎると,県外からの観光客数は減ってしまう傾向がある。
② 県外からの観光客数を増やすには行祭事・イベントの開催数を増やせばよい。
③ 行祭事・イベントの開催数が最も多い県では,行祭事・イベントの開催一回当たりの県外からの観光客数は 6,000 千人を超えている。
④ 県外からの観光客数が多い県ほど,行祭事・イベントを多く開催している傾向がある。
(本問題の図は,「共通基準による観光入込客統計」(観光庁)をもとにして作成している。)
正解と解説
$\boxed{\text{ ソ }}$ ④
⓪ 図より中央値や平均値を正しく求めることは困難である。したがって、不適。
① 行祭事・イベントの開催数と県外からの観光客数には正の相関があることが読み取れる。したがって、不適。
② 行祭事・イベントの開催数が少なくても県外からの観光客数が多い県があることから、必ずしも言えない。したがって、不適。
③ 図より行祭事・イベントの開催数が最も多い県はおよそ145回行い、県外からの観光客数は 6,000 千人を超えているが、一回当たりで計算すると145で割ることになるので、明らかに6,000千人を下回る。したがって、不適。
④ 行祭事・イベントの開催数と県外からの観光客数には正の相関があるので、正しい。
SNSでシェア