【スマホで読む・わかりやすい】共通テスト数学IIB2021第2日程【解説・正解・問題】

第5問　正解

ア　5　イ,ウエ　9,10　オ,カ,キ,ク　2,5,1,2
ケ　4　コ,サ　3,7　シ　－　ス,セ　1.3
ソ,タチ　7,12　ツ　1

(1)

$|\overrightarrow{\text{OA}}|^2=(-1)^2+2^2+0^2$
$=5$

・・・ア

また，点 D は，線分 OA を 9 : 1 に内分するから

$\overrightarrow{\text{OD}}=\cfrac{9}{10}\overrightarrow{\text{OA}}$

これを用いて

$\overrightarrow{\text{CD}}=\overrightarrow{\text{OD}}-\overrightarrow{\text{OC}}$
$=\cfrac{9}{10}\overrightarrow{\text{OA}}-\cfrac{\overrightarrow{\text{OA}}+\overrightarrow{\text{OB}}}{2}$
$=\cfrac{2}{5}\overrightarrow{\text{OA}}-\cfrac{1}{2}\overrightarrow{\text{OB}}$

・・・オ，カ，キ，ク

$\overrightarrow{\text{OA}}\perp\overrightarrow{\text{CD}}$ より

$\overrightarrow{\text{OA}}\cdot\overrightarrow{\text{CD}}=0$
$\overrightarrow{\text{OA}}\cdot\Big(\cfrac{2}{5}\overrightarrow{\text{OA}}-\cfrac{1}{2}\overrightarrow{\text{OB}}\Big)=0$
$\cfrac{2}{5}|\overrightarrow{\text{OA}}|^2-\cfrac{1}{2}\overrightarrow{\text{OA}}\cdot\overrightarrow{\text{OB}}=0$
$\cfrac{2}{5}\cdot5-\cfrac{1}{2}\overrightarrow{\text{OA}}\cdot\overrightarrow{\text{OB}}=0$
$\cfrac{1}{2}\overrightarrow{\text{OA}}\cdot\overrightarrow{\text{OB}}=2$
$\overrightarrow{\text{OA}}\cdot\overrightarrow{\text{OB}}=4$ ・・・①

・・・ケ

問題文に値が示されているが，念のため $|\overrightarrow{\text{OB}}|^2$ の求め方を示しておく。

$\overrightarrow{\text{OB}}\perp\overrightarrow{\text{CE}}$ より

$\overrightarrow{\text{OB}}\cdot\overrightarrow{\text{CE}}=0$
$\overrightarrow{\text{OB}}\cdot(\overrightarrow{\text{OE}}-\overrightarrow{\text{OC}})=0$
$\overrightarrow{\text{OB}}\cdot\Big(\cfrac{3}{5}\overrightarrow{\text{OB}}-\cfrac{1}{2}\overrightarrow{\text{OA}}-\cfrac{1}{2}\overrightarrow{\text{OB}}\Big)=0$
$\cfrac{3}{5}|\overrightarrow{\text{OB}}|^2-\cfrac{1}{2}\overrightarrow{\text{OA}}\cdot\overrightarrow{\text{OB}}-\cfrac{1}{2}|\overrightarrow{\text{OB}}|^2=0$
$\cfrac{1}{10}|\overrightarrow{\text{OB}}|^2-\cfrac{1}{2}\cdot4=0$
$|\overrightarrow{\text{OB}}|^2=20$ ・・・②

①と②より

$\overrightarrow{\text{OA}}\cdot\overrightarrow{\text{OB}}=(-1)\cdot2+2\cdot p+0\cdot q=4$
$-2+2p=4$
$p=3$

また

$|\overrightarrow{\text{OB}}|^2=2^2+p^2+q^2=20$
$4+9+q^2=20$
$q^2=7$
$q=\pm\sqrt{7}$
$q>0$ より，$q=\sqrt{7}$

したがって，B の座標は

$(2,3,\sqrt{7})$

・・・コ，サ

(2)

$\overrightarrow{\text{OH}}=s\overrightarrow{\text{OA}}+t\overrightarrow{\text{OB}}$ より

$\overrightarrow{\text{GH}}=\overrightarrow{\text{OH}}-\overrightarrow{\text{OG}}$
$=-\overrightarrow{\text{OG}}+s\overrightarrow{\text{OA}}+t\overrightarrow{\text{OB}}$

・・・シ

また，$\overrightarrow{\text{GH}}$ を求めると

$\overrightarrow{\text{GH}}=-(4,4,-\sqrt{7})+s(-1,2,0)+t(2,3,\sqrt{7})$
$=(-4-s+2t,-4+2s+3t,\sqrt{7}+\sqrt{7}t)$
$\overrightarrow{\text{GH}}\perp\overrightarrow{\text{OA}}$ より
$\overrightarrow{\text{GH}}\cdot\overrightarrow{\text{OA}}=0$
$(-4-s+2t)\cdot(-1)+(-4+2s+3t)\cdot2+(\sqrt{7}+\sqrt{7}t)\cdot0=0$
$4+s-2t-8+4s+6t=0$
$5s+4t-4=0$

また，$\overrightarrow{\text{GH}}\perp\overrightarrow{\text{OB}}$ より

$\overrightarrow{\text{GH}}\cdot\overrightarrow{\text{OB}}=0$
$(-4-s+2t)\cdot2+(-4+2s+3t)\cdot3+(\sqrt{7}+\sqrt{7}t)\cdot\sqrt{7}=0$
$-8-2s+4t-12+6s+9t+7+7t=0$
$4s+20t-13=0$

式を連立して

$\begin{aligned}25s+20t-20=0\\-)\space4s+20t-13=0\\\hline 21s-7=0\end{aligned}$
$s=\cfrac{1}{3}$

・・・ス，セ

これを代入して

$5\cdot\cfrac{1}{3}+4t-4=0$
$4t-\cfrac{7}{3}=0$
$t=\cfrac{7}{12}$

・・・ソ，タチ

よって

$\overrightarrow{\text{OH}}=\cfrac{1}{3}\overrightarrow{\text{OA}}+\cfrac{7}{12}\overrightarrow{\text{OB}}$

となる。

次に，点 H の位置について考える。

$s=\cfrac{1}{3}$，$t=\cfrac{7}{12}$ として

$s+t=k$ とおくと

$\cfrac{s}{k}+\cfrac{t}{k}=1$

また

$\overrightarrow{\text{OH}}=s\overrightarrow{\text{OA}}+t\overrightarrow{\text{OB}}$
$=\cfrac{s}{k}(k\overrightarrow{\text{OA}})+\cfrac{t}{k}(k\overrightarrow{\text{OB}})$

とする。

$\cfrac{s}{k}=s’$，$\cfrac{t}{k}=t’$ とすると

$\overrightarrow{\text{OH}}=s'(k\overrightarrow{\text{OA}})+t'(k\overrightarrow{\text{OB}})$

また，$s’+t’=1$

さらに

$s+t=k$

$k=\cfrac{1}{3}+\cfrac{7}{12}=\cfrac{11}{12}$ だから

$s’=\cfrac{1}{3}\times\cfrac{12}{11}=\cfrac{4}{11}$
$t’=\cfrac{7}{12}\times\cfrac{12}{11}=\cfrac{7}{11}$

となる。よって

$\overrightarrow{\text{OH}}=\cfrac{4}{11}\cdot\cfrac{11}{12}\overrightarrow{\text{OA}}+\cfrac{7}{11}\cdot\cfrac{11}{12}\overrightarrow{\text{OB}}$
$\overrightarrow{\text{OA’}}=\cfrac{11}{12}\overrightarrow{\text{OA}}$
$\overrightarrow{\text{OB’}}=\cfrac{11}{12}\overrightarrow{\text{OB}}$

とすると

$\overrightarrow{\text{OH}}=\cfrac{4}{11}\overrightarrow{\text{OA’}}+\cfrac{7}{11}\overrightarrow{\text{OB’}}$

つまり，点 H は $\overrightarrow{\text{OA’}}$ と $\overrightarrow{\text{OB’}}$ を 7 : 4 に内分する点である。

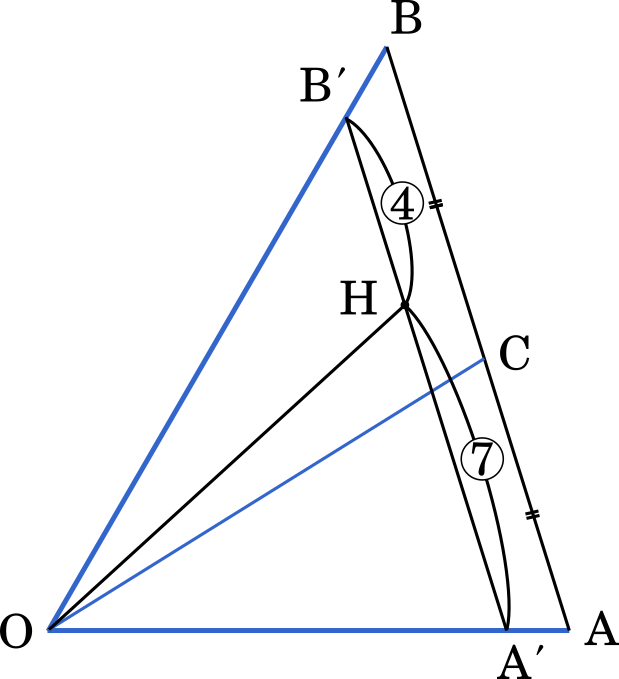
したがって，H は三角形 OBC の内部の点であることがわかる。

・・・ツ

問題文

第3問～第5問は，いずれか2問を選択し，解答しなさい。 

第5問　(選択問題)

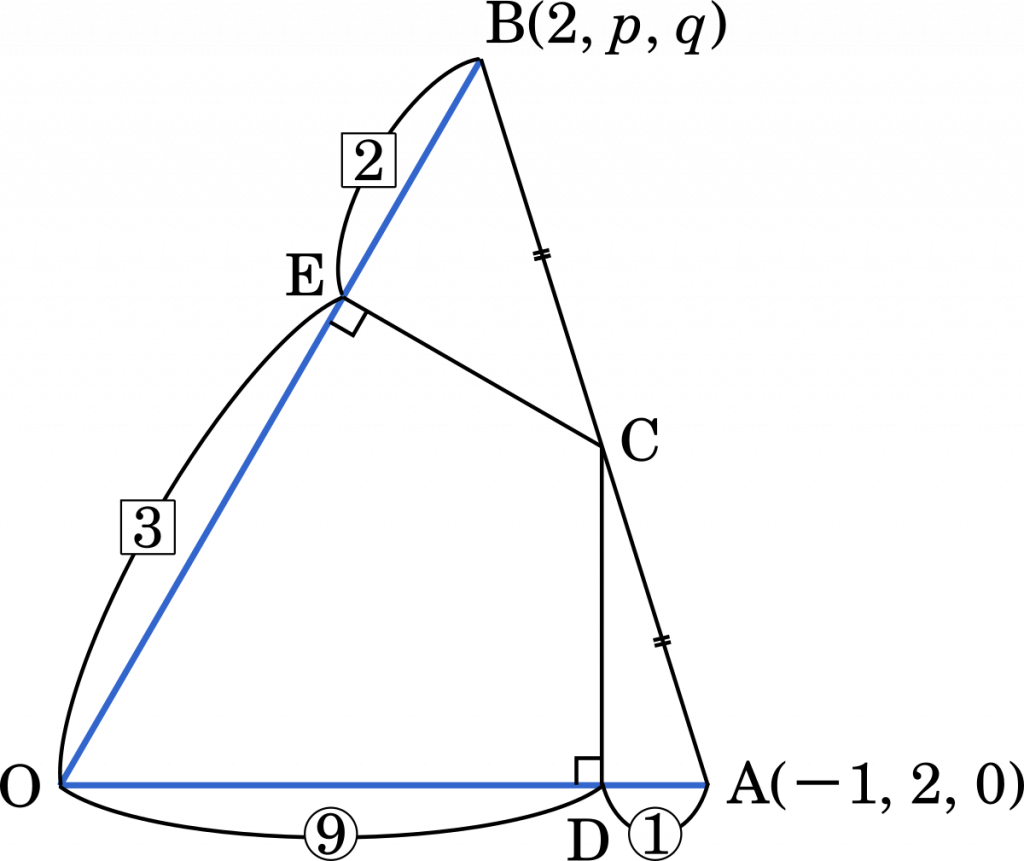
O を原点とする座標空間に 2 点 A$(-1,2,0)$，B$(2,p,q)$ がある。ただし，$q>0$ とする。線分 AB の中点 C から直線 OA に引いた垂線と直線 OA の交点 D は，線分 OA を 9 : 1 に内分するものとする。また，点 C から直線 OB に 引いた垂線と直線 OB の交点 E は，線分 OB を 3 : 2 に内分するものとする。

(1) 点 B の座標を求めよう。

$|\overrightarrow{\text{OA}}|^2=\boxed{\sf{ア}}$ である。また，$\overrightarrow{\text{OD}}=\cfrac{\boxed{\sf{イ}}}{\boxed{\sf{ウエ}}}\overrightarrow{\text{OA}}$ であることにより，$\overrightarrow{\text{CD}}=\cfrac{\boxed{\sf{オ}}}{\boxed{\sf{カ}}}\overrightarrow{\text{OA}}-\cfrac{\boxed{\sf{キ}}}{\boxed{\sf{ク}}}\overrightarrow{\text{OB}}$ と表される。$\overrightarrow{\text{OA}}\perp\overrightarrow{\text{CD}}$ から

$\overrightarrow{\text{OA}}\cdot\overrightarrow{\text{OB}}=\boxed{{\sf{ケ}}}$ ・・・・・・①

である。同様に，$\overrightarrow{\text{CE}}$ を $\overrightarrow{\text{OA}}$，$\overrightarrow{\text{OB}}$ を用いて表すと，$\overrightarrow{\text{OB}}\perp\overrightarrow{\text{CE}}$ から

$|\overrightarrow{\text{OB}}|^2=20$ ・・・・・・②

を得る。 

①と②，および $q>0$ から，B の座標は $(2,\boxed{\sf{コ}},\sqrt{\boxed{\sf{サ}}})$ である。

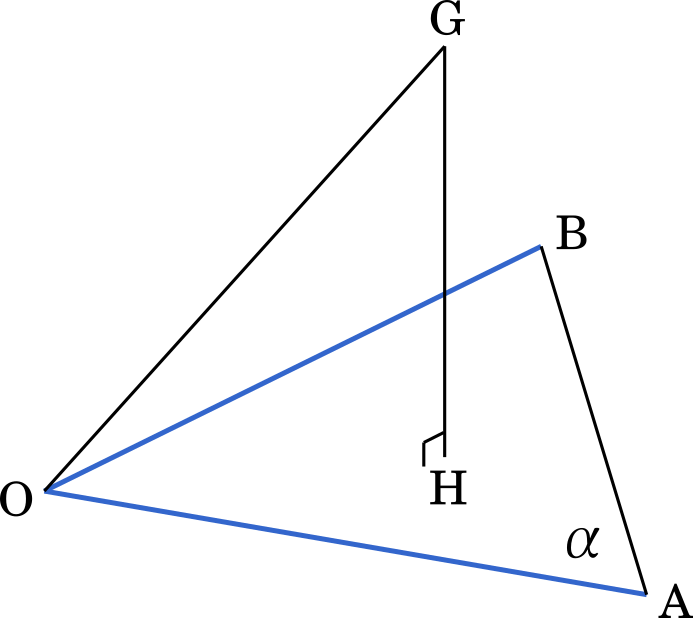
(2) 3 点 O，A，B の定める平面を $\alpha$ とし，点$(4,4,-\sqrt{7})$を G とする。また，$\alpha$ 上に点 H を $\overrightarrow{\text{GH}}\perp\overrightarrow{\text{OA}}$ と $\overrightarrow{\text{GH}}\perp\overrightarrow{\text{OB}}$ が成り立つようにとる。$\overrightarrow{\text{OH}}$ を $\overrightarrow{\text{OA}}$ を $\overrightarrow{\text{OB}}$ 用いて表そう。

H が $\alpha$ 上にあることから，実数 $s$,$t$ を用いて

$\overrightarrow{\text{OH}}=s\overrightarrow{\text{OA}}+t\overrightarrow{\text{OB}}$

と表される。よって

$\overrightarrow{\text{GH}}=\boxed{\sf{シ}}\overrightarrow{\text{OG}}+s\overrightarrow{\text{OA}}+t\overrightarrow{\text{OB}}$

である。これと，$\overrightarrow{\text{GH}}\perp\overrightarrow{\text{OA}}$ および $\overrightarrow{\text{GH}}\perp\overrightarrow{\text{OB}}$ が成り立つことから，$s=\cfrac{\boxed{\sf{ス}}}{\boxed{\sf{セ}}}$，$t=\cfrac{\boxed{\sf{ソ}}}{\boxed{\sf{タチ}}}$ が得られる。ゆえに

$\overrightarrow{\text{OH}}=\cfrac{\boxed{\text{ス}}}{\boxed{\text{セ}}}\overrightarrow{\text{OA}}+\cfrac{\boxed{\text{ソ}}}{\boxed{\text{タチ}}}\overrightarrow{\text{OB}}$

となる。また，このことから，H は $\boxed{\boxed{\sf{ツ}}}$ であることがわかる。

$\boxed{\boxed{\text{ツ}}}$ の解答群

⓪ 三角形 OAC の内部の点
① 三角形 OBC の内部の点
② 点O，Cと異なる，線分 OC 上の点
④ 三角形 OAB の周上の点
④ 三角形 OAB の内部にも周上にもない点