【スマホで読む・わかりやすい】共通テスト数学IIB2021第2日程【解説・正解・問題】

第2問　正解

ア　2　イ　2　ウ　0　エ　1　オ,カ　1,3
キ　2　ク　a　ケ　0　コ　2　サ　1
シス　－c　セ　c　ソ,タ,チ,ツ　－,3,3,6
テ　2
＊第2問コでbと解答した場合，第2問キで2と解答しているときにのみ3点を与える。

〔1〕(1)

$a=1$ のとき

$f(x)=(x-1)(x-2)$

公式　$\displaystyle\cfrac{d}{dx}\int_a^xf(t)\space dt=f(x)$　より

$\displaystyle F'(x)=\cfrac{d}{dx}\int_0^x f(t)\space dt=f(x)$
$=(x-1)(x-2)$

ここで，$(x-1)(x-2)=0$ とすると

$x=1,2$

よって，$F(x)$ は $x=1,2$ で極値をとる。

増減表は

$\def\arraystretch{1.5}\begin{array}{|c|c|c|c|c|c|}\hline x&\cdots&1&\cdots&2&\cdots\\\hline F'(x)&+&0&-&0&+\\\hline F(x)&\nearrow&\sf{極大}&\searrow&\sf{極小}&\nearrow\\\hline\end{array}$

したがって，$F(x)$ は $x=2$ で極小になる。

・・・ア

〔1〕(2)

公式より

$\displaystyle F'(x)=\cfrac{d}{dx}\int_0^x f(t)\space dt=f(x)$
$=(x-a)(x-2)$

$F(x)$ がつねに増加するとき，すべての $x$ において $F'(x)\geqq0$ が成り立つ。

$(x-a)(x-2)\geqq0$ として

$x^2-(a+2)x+2a\geqq0$

このとき，判別式 $D\leqq0$ が成り立つ。

$D=(a+2)^2-8a\leqq0$
$a^2+4a+4-8a\leqq0$
$a^2-4a+4\leqq0$
$(a-2)^2\leqq0$

不等式が成り立つのは $a=2$ のときのみである。したがって

$a=2$

・・・イ

また

$\displaystyle F(0)=\int_0^0 f(t)\space dt=0$

・・・ウ

であるから，$a=2$ のとき

$f(x)=(x-2)^2$

$\displaystyle F(x)=\int_0^x(t-2)^2\space dt$
$\displaystyle F(2)=\int_0^2(t-2)^2\space dt$

$F(x)$ はつねに増加するので，$F(2)$ の値は正である。

・・・エ

（補足）

ここで，$F(0)=0$ を確認しているのは，仮に $F(0)$ が負の値であるとすると，関数がつねに増加したとしても，$F(2)$ が必ずしも正の値になるとは限らないからである。

（補足終わり）

〔1〕(3)

$a>2$ として

$\displaystyle G(x)=\int_b^x f(t)\space dt$
$=\displaystyle\int_0^x f(t)\space dt-\int_0^b f(t)\space dt$
$=F(x)-F(b)$

したがって，関数 $y=G(x)$ のグラフは，$y=F(x)$ のグラフを $y$ 軸方向に $-F(b)$ だけ平行移動したものと一致する。

・・・オ，カ

また，$G(x)$ を $x$ で微分すると

$\displaystyle G'(x)=\cfrac{d}{dx}\int_b^x f(t)\space dt=f(x)$

$f(x)=(x-a)(x-2)=0$ とすると

$x=a,2$

$a>2$ であることに注意して，増減表は

$\def\arraystretch{1.5}\begin{array}{|c|c|c|c|c|c|}\hline x&\cdots&2&\cdots&a&\cdots\\\hline G'(x)&+&0&-&0&+\\\hline G(x)&\nearrow&\sf{極大}&\searrow&\sf{極小}&\nearrow\\\hline\end{array}$

したがって，$G(x)$ は $x=2$ で極大になり，$x=a$ で極小になる。

・・・キ，ク

また

$\displaystyle G(b)=\int_b^b f(t)\space dt=0$

・・・ケ

であるから，$b=2$ のとき

$\displaystyle G(x)=\int_2^x f(t)\space dt$
$\displaystyle G(2)=\int_2^2 f(t)\space dt=0$

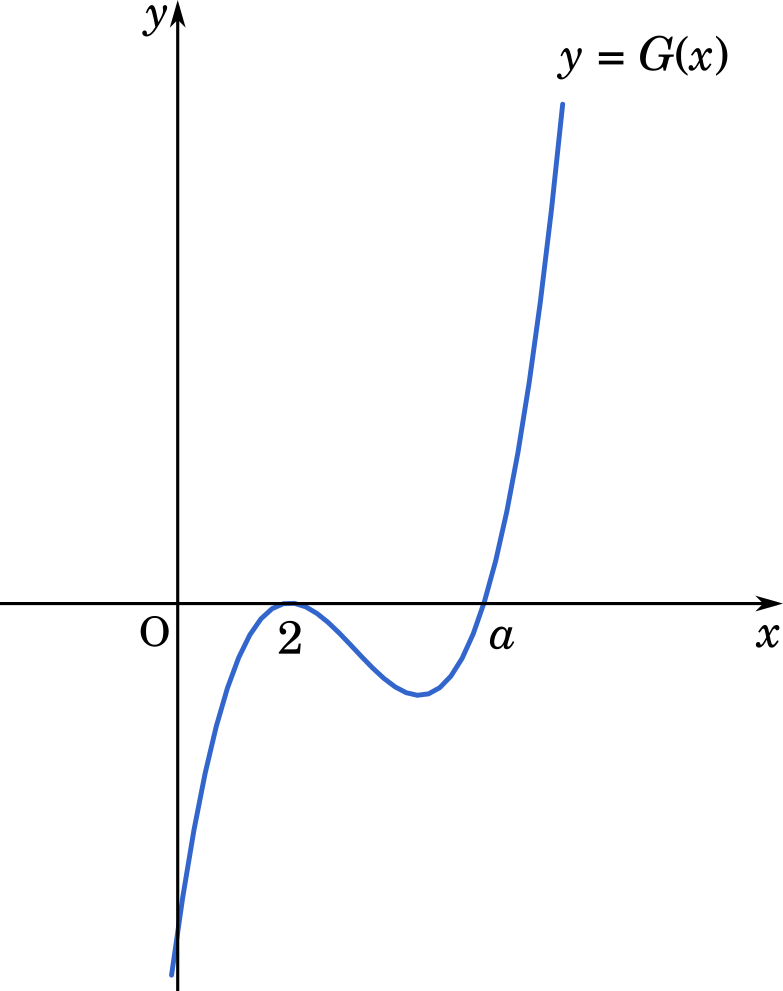
したがって，曲線 $y=G(x)$ と $x$ との共有点の個数は 2 個である。

・・・コ

〔2〕

$g(x)=|x|(x+1)$ とおく。

$x<0$ のとき

$g(x)=-x(x+1)=-x^2-x$

式を微分すると

$g'(x)=-2x-1$

したがって

$g'(-1)=-2(-1)-1=1$

・・・サ

直線 $\ell$ を求めると，点 P$(-1,0)$ を通り，傾きが $c$ だから

$\ell:y=c(x+1)=cx+c$

また，$x\geqq0$ のとき

$g(x)=x(x+1)=x^2+x$

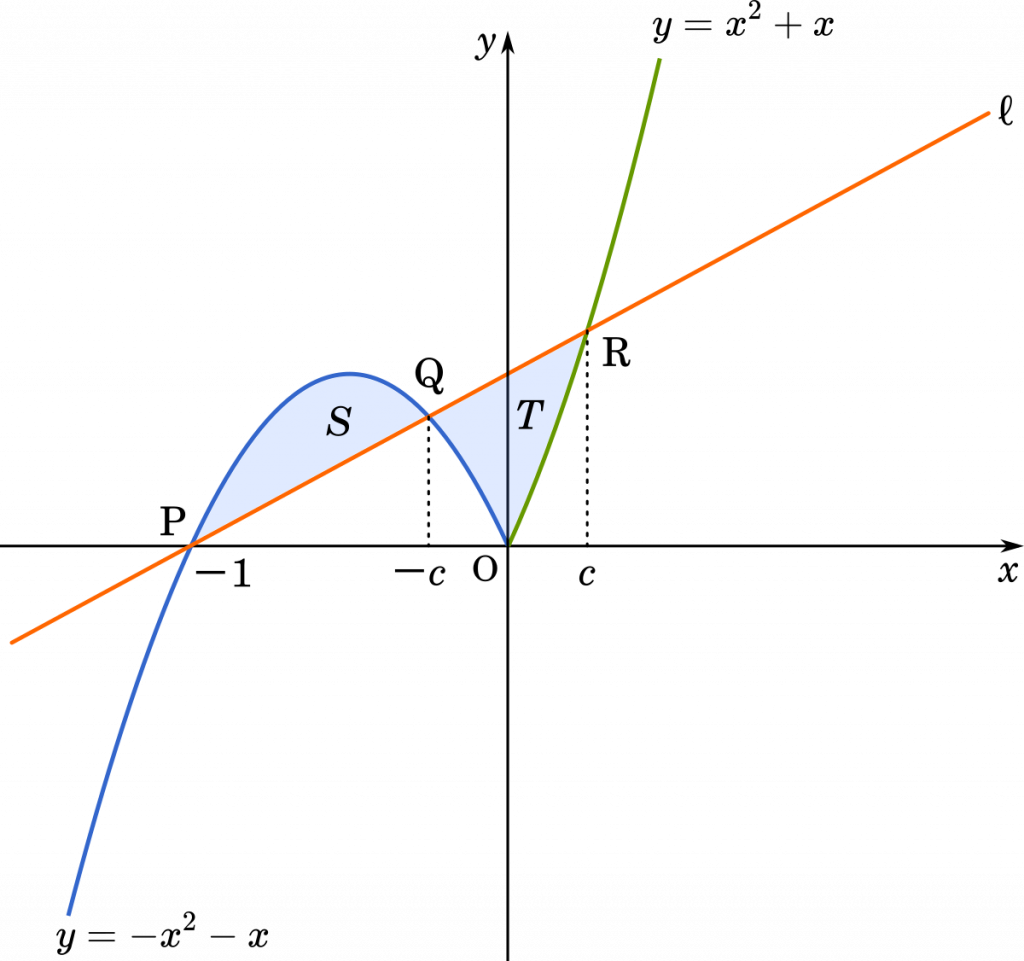
次に，点 Q は $g(x)=-x^2-x$ と直線 $\ell$ の交点の一つだから

$cx+c=-x^2-x$
$x^2+cx+x+c=0$
$x^2+(c+1)x+c=0$

このとき，もう一つの交点 P から，$x=-1$ は方程式の解の一つである。

ここで，解と係数の関係を用いると良い。

よって

$-1\cdot\beta=c$
$\beta=-c$

したがって，点 Q の $x$ 座標は $-c$ である。

・・・シス

また，点 R の $x$ 座標は正の値であることに注意して，交点を求めると

$cx+c=x^2+x$
$x^2+(1-c)x-c=0$
$x=\cfrac{c-1\pm\sqrt{(1-c)^2+4c}}{2}$
$=\cfrac{c-1\pm\sqrt{1-2c+c^2+4c}}{2}$
$=\cfrac{c-1\pm\sqrt{c^2+2c+c^2}}{2}$
$=\cfrac{c-1\pm\sqrt{(c+1)^2}}{2}$

ここで $0<c<1$ だから $c+1$ は正の数である。よって，$\sqrt{(c+1)^2}=c+1$ が成り立つ。

$=\cfrac{c-1\pm(c+1)}{2}$
$=\cfrac{2c}{2}$，$\cfrac{-2}{2}$
$=c,-1$

$x>0$ より $x=c$

・・・セ

さらに，直線 $\ell$ と曲線で囲まれた面積を求める。

$\displaystyle S=\int_{-1}^{-c} -x^2-x-cx-c\space dx$
$\displaystyle =\int_{-1}^{-c}-x^2-(c+1)x-c\space dx$
$=\Big[-\cfrac{x^3}{3}-\cfrac{c+1}{2}x^2-cx\Big]_{-1}^{-c}$
$=\cfrac{c^3}{3}-\cfrac{(c+1)c^2}{2}+c^2-\Big(\cfrac{1}{3}-\cfrac{c+1}{2}+c\Big)$
$=\cfrac{2c^3-3(c+1)c^2+6c^2-2+3(c+1)-6c}{6}$
$=\cfrac{2c^3-3c^3-3c^2+6c^2-2+3c+3-6c}{6}$
$=\cfrac{-c^2+3c^2-3c+1}{6}$

・・・ソ，タ，チ，ツ

また $T$ の面積は，図形を $y$ 軸で区切って，それぞれの面積を足し合わせると良い。

$\displaystyle T_1=\int_{-c}^0 cx+c+x^2+x\space dx$

ここで積分区間を逆にすると計算ミスを減らすことができる。

$\displaystyle=\int_0^{-c}-x^2-(c+1)x-c\space dx$
$=\Big[-\cfrac{x^3}{3}-\cfrac{c+1}{2}x^2-cx\Big]_0^{-c}$
$=\cfrac{c^3}{3}-\cfrac{(c+1)c^2}{2}+c^2$

また

$\displaystyle T_2=\int_0^c cx+c-x^2-x\space dx$
$\displaystyle=\int_0^c-x^2+(c-1)x+c\space dx$
$=\Big[-\cfrac{x^3}{3}+\cfrac{c-1}{2}x^2+cx\Big]_0^c$
$=-\cfrac{c^3}{3}+\cfrac{(c-1)c^2}{2}+c^2$

したがって

$T=T_1+T_2$
$=\cfrac{c^3}{3}-\cfrac{(c+1)c^2}{2}+c^2-\cfrac{c^3}{3}+\cfrac{(c-1)c^2}{2}+c^2$
$=\cfrac{-c^3-c^2+2c^2+c^3-c^2+2c^2}{2}$
$=\cfrac{2c^2}{2}=c^2$

・・・テ

問題文

第2問

(必答問題)

〔1〕 $a$ を実数とし，$f(x)=(x-a)(x-2)$ とおく。また，$\displaystyle F(x)=\int_0^x f(t)\space dt$ とする。

(1) $a=1$ のとき，$F(x)$ は $x=\boxed{\sf{ア}}$ で極小になる。

(2) $a=\boxed{\sf{イ}}$ のとき，$F(x)$ はつねに増加する。また，$F(0)=\boxed{\sf{ウ}}$ であるから，$a=\boxed{\text{イ}}$ のとき，$F(2)$ の値は，$\boxed{\boxed{\sf{エ}}}$ である。

$\boxed{\boxed{\text{エ}}}$ の解答群 

⓪ $0$ ① 正 ② 負

(3) $a>\boxed{\text{イ}}$ とする。

$b$ を実数とし，$\displaystyle G(x)=\int_b^xf(t)\space dt$ とおく。

関数 $y=G(x)$ のグラフは，$y=F(x)$ のグラフを $\boxed{\boxed{\sf{オ}}}$ 方向に $\boxed{\boxed{\sf{カ}}}$ だけ平行移動したものと一致する。また，$G(x)$ は $x=\boxed{\sf{キ}}$ で極大になり，$x=\boxed{\sf{ク}}$ で極小になる。

$G(b)=\boxed{\sf{\\ケ}}$ であるから，$b=\boxed{\text{キ}}$ のとき，曲線 $y=G(x)$ と $x$ 軸との共有点の個数は，$\boxed{\sf{コ}}$ 個である。

$\boxed{\boxed{\text{オ}}}$ の解答群

⓪ $x$軸　① $y$軸

$\boxed{\boxed{\text{カ}}}$ の解答群

⓪ $b$　① $-b$　② $F(b)$
③ $-F(b)$　④ $F(-b)$　⑤ $-F(-b)$

〔２〕 $g(x)=|x|(x + 1)$ とおく。

点 P$(-1, 0)$ を通り，傾きが $c$ の直線を $\ell$ とする。$g'(-1)=\boxed{\sf{サ}}$ であるから，$0<c<\boxed{\text{サ}}$ のとき，曲線 $y=g(x)$ と直線 $\ell$ とは 3 点で交わる。そのうちの 1 点は P であり，残りの 2 点を点 P に近い方から順に Q，R とすると，点 Q の $x$ 座標は $\boxed{\sf{シス}}$ であり，点 R の $x$ 座標は $\boxed{\sf{セ}}$ である。

また，$0<c<\boxed{\text{サ}}$ のとき，線分 PQ と曲線 $y=g(x)$ で囲まれた図形の面積を $S$ とし，線分 QR と曲線 $y=g(x)$ で囲まれた図形の面積を $T$ とすると

$S=\cfrac{\boxed{\sf{ソ}}c^3+\boxed{\sf{タ}}c^2-\boxed{\sf{チ}}c+1}{\boxed{\sf{ツ}}}$
$T=c^{\boxed{\sf{テ}}}$

である。