【スマホで読む・わかりやすい】共通テスト数学IIB2021本試【解説・正解・問題】
第5問 正解
アイ 36 ウ a エ,オ a,1
カ,キ,ク 3,5,2 ケ,コ,サ 1,5,4
シ 9 ス 0 セ 0
(1)
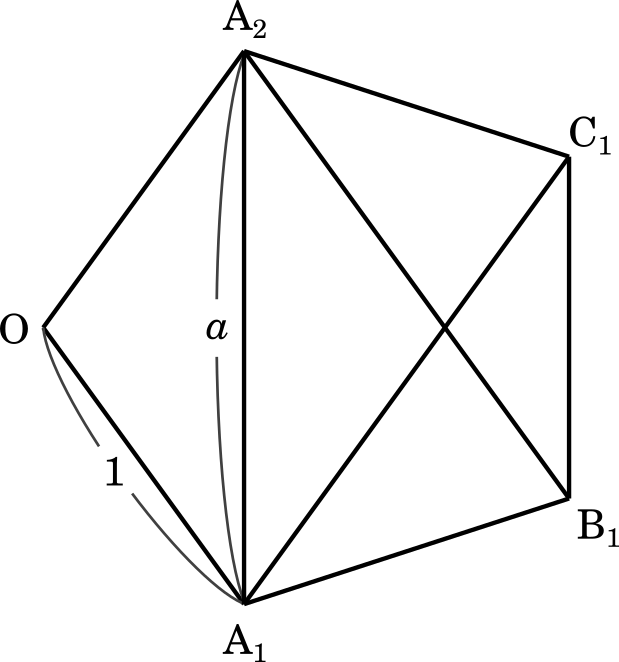
正五角形の内角は
$180\degree\times(5-2)=540\degree$
$540\degree\div5=108\degree$
三角形 $\text A_1\text B_1\text C_1$ は $\text B_1\text A_1=\text B_1\text C_1$ の二等辺三角形だから,底角は
$\angle\text A_1\text C_1\text B_1=(180\degree-108\degree)\div2$
$=72\degree\div2=36\degree$
・・・アイ
$\overrightarrow{\text A_1\text A_2}$ と $\overrightarrow{\text B_1\text C_1}$ は平行であり,かつ
$|\overrightarrow{\text A_1\text A_2}|=a$
$|\overrightarrow{\text B_1\text C_1}|=1$
よって
$\overrightarrow{\text A_1\text A_2}=a\overrightarrow{\text B_1\text C_1}$
・・・ウ
$\overrightarrow{\text B_1\text C_1}=\cfrac{1}{a}\overrightarrow{\text A_1\text A_2}=\cfrac{1}{a}(\overrightarrow{\text{OA}_2}-\overrightarrow{\text{OA}_1})$
また
$\overrightarrow{\text{B}_1\text{C}_1}=\overrightarrow{\text{B}_1\text{A}_2}+\overrightarrow{\text{A}_2\text{O}}+\overrightarrow{\text{O}\text{A}_1}+\overrightarrow{\text{A}_1\text{C}_1}$
$=-a\overrightarrow{\text{OA}_1}-\overrightarrow{\text{OA}_2}+\overrightarrow{\text{OA}_1}+a\overrightarrow{\text{OA}_2}$
$=+a\overrightarrow{\text{OA}_2}-\overrightarrow{\text{OA}_2}-a\overrightarrow{\text{OA}_1}+\overrightarrow{\text{OA}_1}$
$=(a-1)\overrightarrow{\text{OA}_2}-(a-1)\overrightarrow{\text{OA}_1}$
$=(a-1)(\overrightarrow{\text{OA}_2}-\overrightarrow{\text{OA}_1})$
・・・エオ
となるので
$\cfrac{1}{a}=(a-1)$
が成り立つ。$a>0$ だから,両辺に $a$ をかけて
$1=a(a-1)$
$a^2-a-1=0$
$a=\cfrac{1\pm\sqrt{1+4}}{2}$
$=\cfrac{1\pm\sqrt{5}}{2}$
$a>0$ より
$a=\cfrac{1+\sqrt{5}}{2}$
(2)

$\overrightarrow{\text{O}\text{B}_1}=\overrightarrow{\text{O}\text{A}_2}+\overrightarrow{\text{A}_2\text{B}_1}=\overrightarrow{\text{O}\text{A}_2}+a\overrightarrow{\text{O}\text{A}_1}$
また
$|\overrightarrow{\text{OA}_2}-\overrightarrow{\text{OA}_1}|^2=|\overrightarrow{\text A_1\text A_2}|^2$
(1)より,$|\overrightarrow{\text A_1\text A_2}|=a$ だから
$|\overrightarrow{\text A_1\text A_2}|^2=a^2=\Big(\cfrac{1+\sqrt{5}}{2}\Big)^2$
$=\cfrac{1+2\sqrt{5}+5}{4}=\cfrac{6+2\sqrt{5}}{4}$
$=\cfrac{3+\sqrt{5}}{2}$
・・・カ,キ,ク
また
$|\overrightarrow{\text{OA}_2}-\overrightarrow{\text{OA}_1}|^2$ を展開すると
$|\overrightarrow{\text{OA}_2}-\overrightarrow{\text{OA}_1}|^2=|\overrightarrow{\text{OA}_2}|^2-2\overrightarrow{\text{OA}_1}\cdot\overrightarrow{\text{OA}_2}+|\overrightarrow{\text{OA}_1}|^2$ $|\overrightarrow{\text{OA}_1}|=|\overrightarrow{\text{OA}_2}|=1$ だから
$\cfrac{3+\sqrt{5}}{2}=1-2\overrightarrow{\text{OA}_1}\cdot\overrightarrow{\text{OA}_2}+1$
$2\overrightarrow{\text{OA}_1}\cdot\overrightarrow{\text{OA}_2}=2-\cfrac{3+\sqrt{5}}{2}$
$2\overrightarrow{\text{OA}_1}\cdot\overrightarrow{\text{OA}_2}=\cfrac{1-\sqrt{5}}{2}$
$\overrightarrow{\text{OA}_1}\cdot\overrightarrow{\text{OA}_2}=\cfrac{1-\sqrt{5}}{4}$
・・・ケ,コ,サ
さらに
$\overrightarrow{\text{O}\text{B}_2}=\overrightarrow{\text{O}\text{A}_3}+a\overrightarrow{\text{O}\text{A}_2}$
$\overrightarrow{\text{O}\text{A}_2}\cdot\overrightarrow{\text{O}\text{A}_3}=\overrightarrow{\text{O}\text{A}_3}\cdot\overrightarrow{\text{O}\text{A}_1}=\cfrac{1-\sqrt{5}}{4}$
を用いて
$\overrightarrow{\text{O}\text{A}_1}\cdot\overrightarrow{\text{O}\text{B}_2}=\overrightarrow{\text{O}\text{A}_1}\cdot(\overrightarrow{\text{O}\text{A}_3}+a\overrightarrow{\text{O}\text{A}_2})$
$=\overrightarrow{\text{O}\text{A}_1}\cdot\overrightarrow{\text{O}\text{A}_3}+a\overrightarrow{\text{O}\text{A}_1}\cdot\overrightarrow{\text{O}\text{A}_2}$
$=\cfrac{1-\sqrt{5}}{4}+a\Big(\cfrac{1-\sqrt{5}}{4}\Big)$
$=\cfrac{1-\sqrt{5}}{4}\cdot(1+a)$
$=\cfrac{1-\sqrt{5}}{4}\cdot\Big(1+\cfrac{1+\sqrt{5}}{2}\Big)$
$=\cfrac{1-\sqrt{5}}{4}\cdot\cfrac{3+\sqrt{5}}{2}$
$=\cfrac{(1-\sqrt{5})(3+\sqrt{5})}{8}$
$=\cfrac{3+\sqrt{5}-3\sqrt{5}-5}{8}$
$=\cfrac{-2-2\sqrt{5}}{8}$
$=\cfrac{-1-\sqrt{5}}{4}$
・・・シ
また
$\overrightarrow{\text{O}\text{B}_1}\cdot\overrightarrow{\text{O}\text{B}_2}=(\overrightarrow{\text{O}\text{A}_2}+a\overrightarrow{\text{O}\text{A}_1})\cdot(\overrightarrow{\text{O}\text{A}_3}+a\overrightarrow{\text{O}\text{A}_2})$
$=\overrightarrow{\text{O}\text{A}_2}\cdot\overrightarrow{\text{O}\text{A}_3}+a|\overrightarrow{\text{O}\text{A}_2}|^2+a\overrightarrow{\text{O}\text{A}_1}\cdot\overrightarrow{\text{O}\text{A}_3}+a^2\overrightarrow{\text{O}\text{A}_1}\cdot\overrightarrow{\text{O}\text{A}_2}$
$=\cfrac{1-\sqrt{5}}{4}+a\cdot1+a\cdot\cfrac{1-\sqrt{5}}{4}+a^2\cdot\cfrac{1-\sqrt{5}}{4}$
$=\cfrac{1-\sqrt{5}}{4}(a^2+a+1)+a$
$=\cfrac{1-\sqrt{5}}{4}\Big\{\Big(\cfrac{1+\sqrt{5}}{2}\Big)^2+\cfrac{1+\sqrt{5}}{2}+1\Big\}+\cfrac{1+\sqrt{5}}{2}$
$=\cfrac{1-\sqrt{5}}{4}\Big(\cfrac{1+2\sqrt{5}+5}{4}+\cfrac{1+\sqrt{5}}{2}+1\Big)+\cfrac{1+\sqrt{5}}{2}$
$=\cfrac{1-\sqrt{5}}{4}\Big(\cfrac{3+\sqrt{5}}{2}+\cfrac{1+\sqrt{5}}{2}+1\Big)+\cfrac{1+\sqrt{5}}{2}$
$=\cfrac{1-\sqrt{5}}{4}\cdot(3+\sqrt{5})+\cfrac{1+\sqrt{5}}{2}$
$=\cfrac{(1-\sqrt{5})(3+\sqrt{5})}{4}+\cfrac{1+\sqrt{5}}{2}$
$=\cfrac{3+\sqrt{5}-3\sqrt{5}-5}{4}+\cfrac{1+\sqrt{5}}{2}$
$=\cfrac{-1-\sqrt{5}}{2}+\cfrac{1+\sqrt{5}}{2}$
$=0$
・・・ス
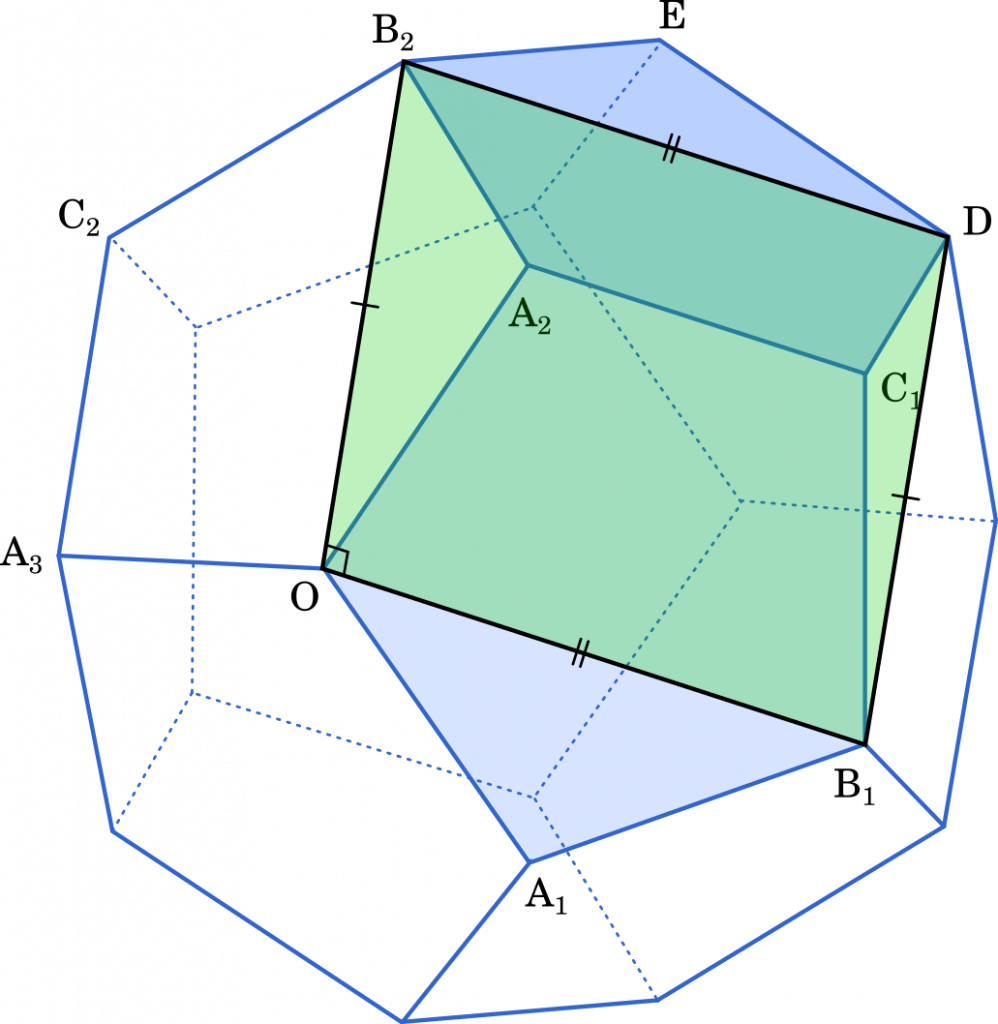
最後に
$\overrightarrow{\text B_2\text D}=a\overrightarrow{\text A_2\text C_1}=\overrightarrow{\text{OB}_1}$
だから,$\text B_2\text D$ と $\text{OB}_1$ は長さが $a$ で等しく,かつ平行である。
また $\overrightarrow{\text{O}\text{B}_1}\cdot\overrightarrow{\text{O}\text{B}_2}=0$ であることから
$\angle\text B_1\text O\text B_2=90\degree$
さらに,$\text{OB}_2=\text B_1\text C_1=a$ だから
したがって,$\text{OB}_1\text{DB}_2$ は正方形であることがわかる。
・・・セ
問題文
第3問~第5問は,いずれか2問を選択し,解答しなさい。
第5問
1 辺の長さが 1 の正五角形の対角線の長さを $a$ とする。
(1) 1 辺の長さが 1 の正五角形 $\text{OA}_1\text{B}_1\text{C}_1\text{A}_2$ を考える。
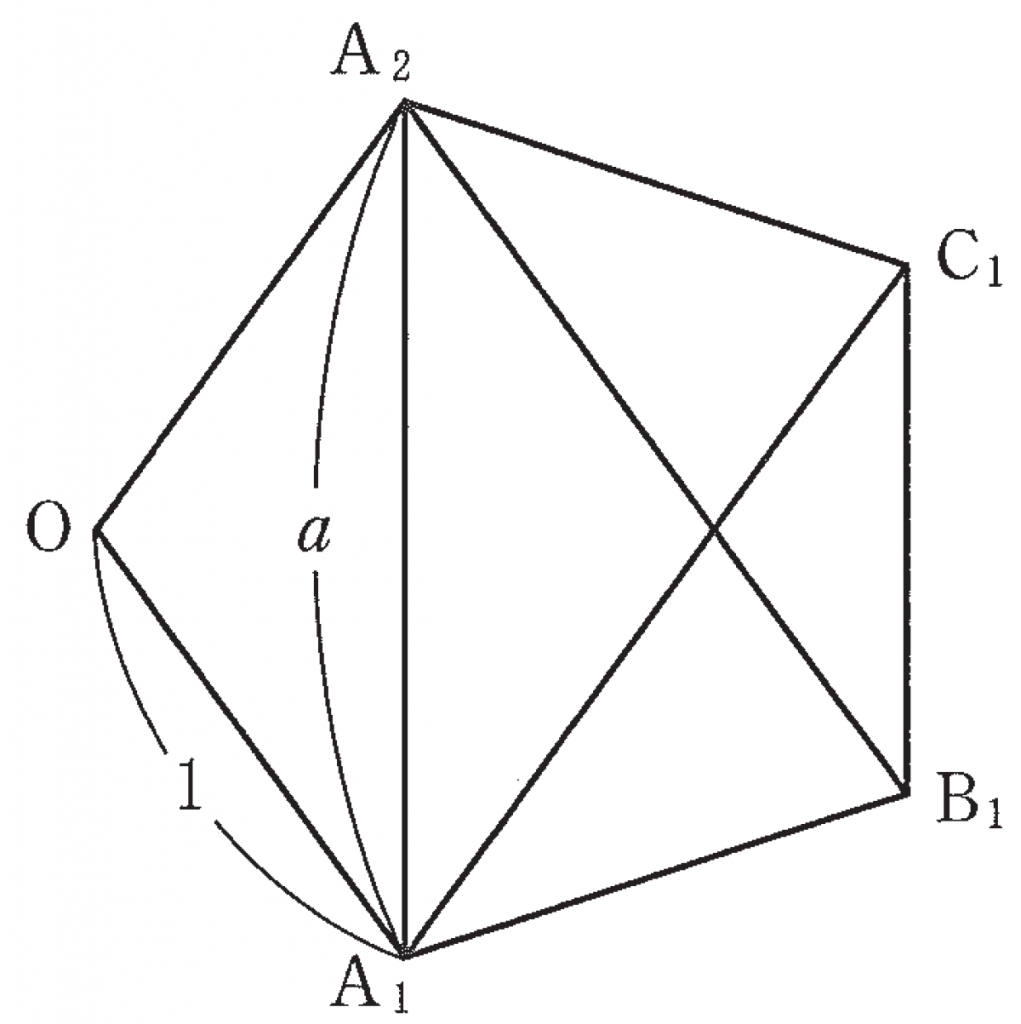
$\angle\text{A}_1\text{C}_1\text{B}_1=\boxed{\sf アイ}\degree$,$\angle\text{C}_1\text{A}_1\text{A}_2=\boxed{\text アイ}\degree$ となることから,$\overrightarrow{\text{A}_1\text{A}_2}$ と $\overrightarrow{\text{B}_1\text{C}_1}$ は平行である。ゆえに
$\overrightarrow{\text{A}_1\text{A}_2}=\boxed{\sf ウ}\space\overrightarrow{\text{B}_1\text{C}_1}$
であるから
$\overrightarrow{\text{B}_1\text{C}_1}=\cfrac{1}{\boxed{\text ウ}}\space\overrightarrow{\text{A}_1\text{A}_2}=\cfrac{1}{\boxed{\text ウ}}(\overrightarrow{\text{OA}_2}-\overrightarrow{\text{OA}_1})$
また,$\overrightarrow{\text{OA}_1}$ と $\overrightarrow{\text{A}_2\text{B}_1}$ は平行で,さらに,$\overrightarrow{\text{OA}_2}$ と $\overrightarrow{\text{A}_1\text{C}_1}$ も平行であることから
$\overrightarrow{\text{B}_1\text{C}_1}=\overrightarrow{\text{B}_1\text{A}_2}+\overrightarrow{\text{A}_2\text{O}}+\overrightarrow{\text{O}\text{A}_1}+\overrightarrow{\text{A}_1\text{C}_1}$
$=-\boxed{\text ウ}\space\overrightarrow{\text{O}\text{A}_1}-\overrightarrow{\text{O}\text{A}_2}+\overrightarrow{\text{O}\text{A}_1}+\boxed{\text ウ}\space\overrightarrow{\text{O}\text{A}_2}$
$=(\boxed{\sf エ}-\boxed{\sf オ})(\overrightarrow{\text{O}\text{A}_2}-\overrightarrow{\text{O}\text{A}_1})$
となる。したがって
$\cfrac{1}{\boxed{\text ウ}}=\boxed{\text エ}-\boxed{\text オ}$
が成り立つ。$a>0$ に注意してこれを解くと,$a=\cfrac{1+\sqrt{5}}{2}$ を得る。
(2) 下の図のような, 1辺の長さが1の正十二面体を考える。正十二面体とは,どの面もすべて合同な正五角形であり,どの頂点にも三つの面が集まっているへこみのない多面体のことである。
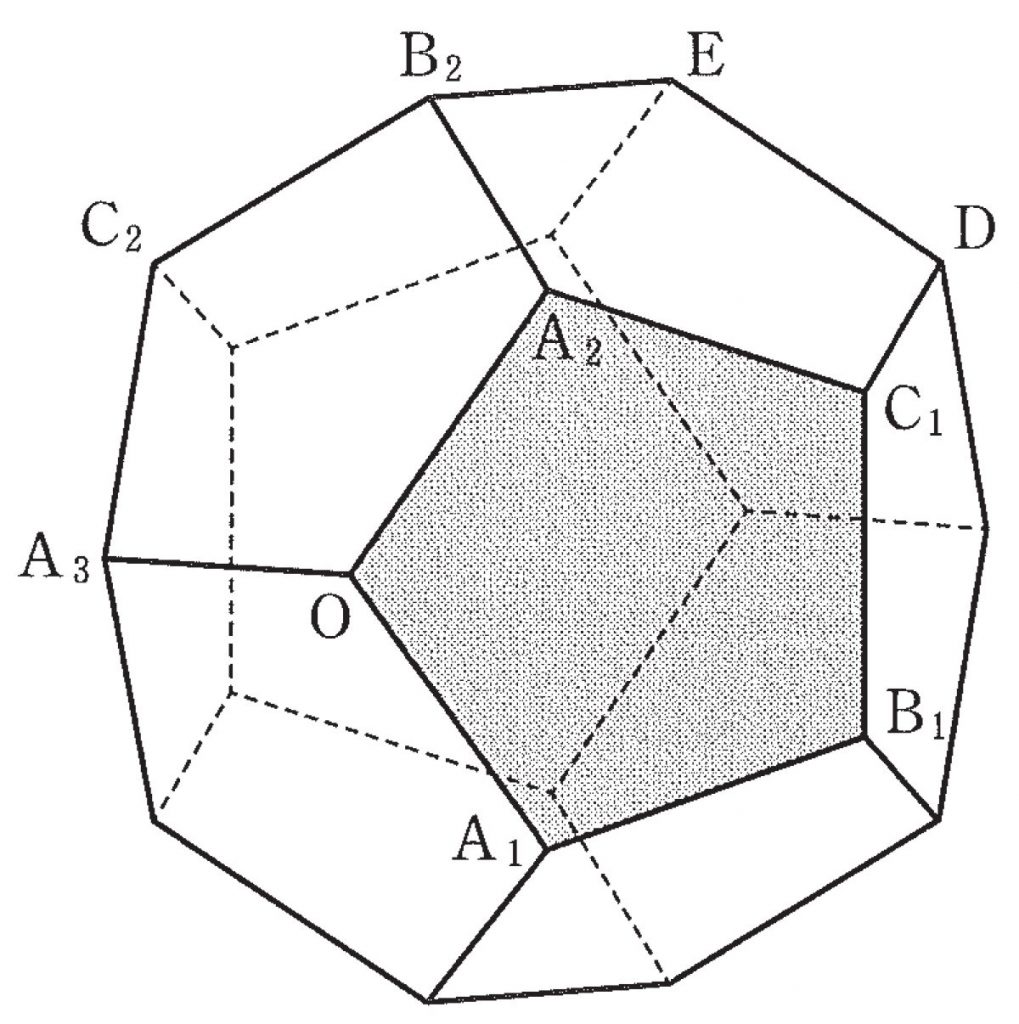
面 $\text{OA}_1\text B_1\text C_1\text A_2$ に着目する。$\overrightarrow{\text{O}\text{A}_1}$ と $\overrightarrow{\text{A}_2\text{B}_1}$ が平行であることから
$\overrightarrow{\text{O}\text{B}_1}=\overrightarrow{\text{O}\text{A}_2}+\overrightarrow{\text{A}_2\text{B}_1}=\overrightarrow{\text{O}\text{A}_2}+\boxed{\text ウ}\space\overrightarrow{\text{O}\text{A}_1}$
である。また
$|\overrightarrow{\text{O}\text{A}_2}-\overrightarrow{\text{O}\text{A}_1}|^2=|\overrightarrow{\text{A}_1\text{A}_2}|^2=\cfrac{\boxed{\sf カ}\sqrt{\boxed{\sf キ}}}{\boxed{\sf ク}}$
に注意すると
$\overrightarrow{\text{O}\text{A}_1}\cdot\overrightarrow{\text{O}\text{A}_2}=\cfrac{\boxed{\sf ケ}-\sqrt{\boxed{\sf コ}}}{\boxed{\sf サ}}$
を得る。
だたし,$\boxed{\text カ}$~$\boxed{\text サ}$ は,文字 $a$ を用いない形で答えること。
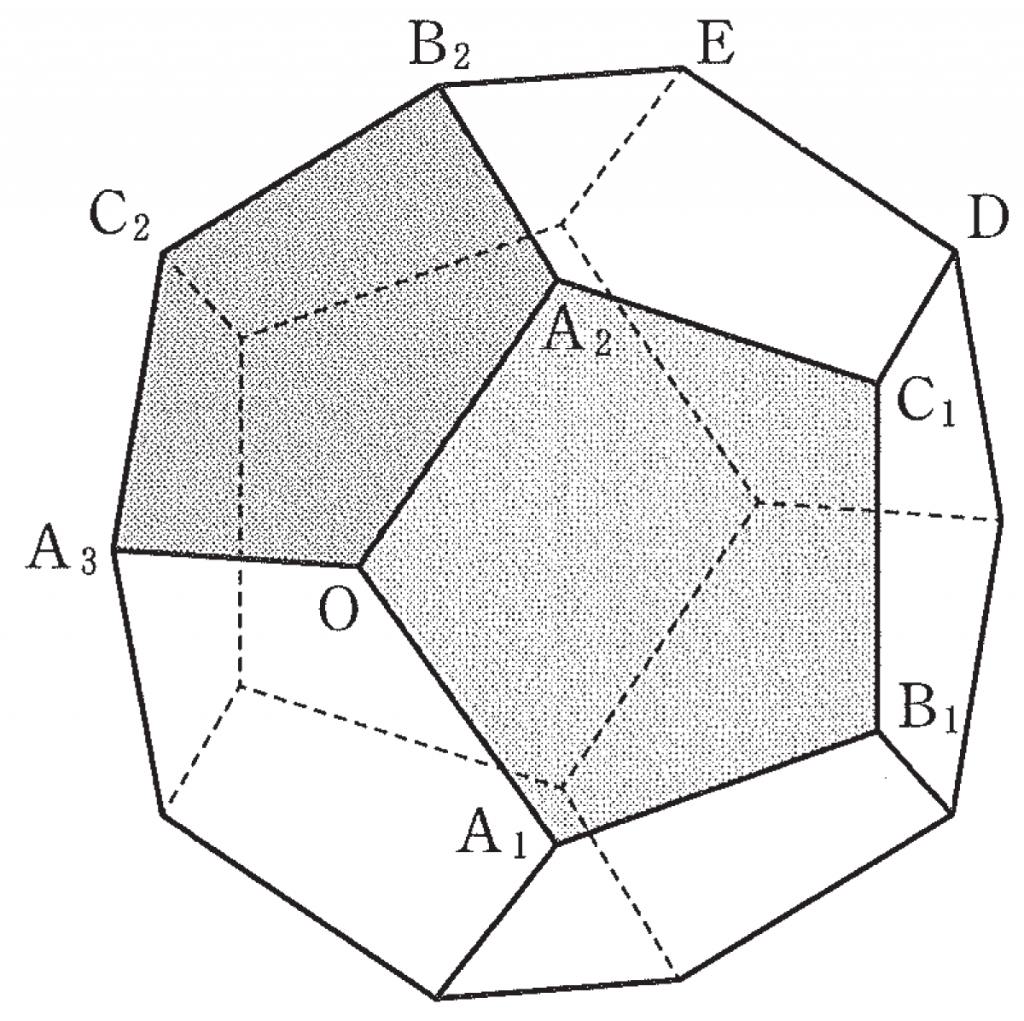
次に,面 $\text{OA}_2\text B_2\text C_2\text A_3$ に着目すると
$\overrightarrow{\text{O}\text{B}_2}=\overrightarrow{\text{O}\text{A}_3}+\boxed{\text ウ}\space\overrightarrow{\text{O}\text{A}_2}$
である。さらに
$\overrightarrow{\text{O}\text{A}_2}\cdot\overrightarrow{\text{O}\text{A}_3}=\overrightarrow{\text{O}\text{A}_3}\cdot\overrightarrow{\text{O}\text{A}_1}=\cfrac{\boxed{\sf ケ}-\sqrt{\boxed{\sf コ}}}{\boxed{\sf サ}}$
が成り立つことがわかる。ゆえに
$\overrightarrow{\text{O}\text{A}_1}\cdot\overrightarrow{\text{O}\text{B}_2}=\boxed{\boxed{\sf シ}}$,$\overrightarrow{\text{O}\text{B}_1}\cdot\overrightarrow{\text{O}\text{B}_2}=\boxed{\boxed{\sf ス}}$
である。
$\boxed{\boxed{\text シ}}$,$\boxed{\boxed{\text ス}}$ の解答群(同じものを繰り返し選んでもよい。)
⓪ $0$ ① $1$ ② $-1$
③ $\cfrac{1+\sqrt{5}}{2}$ ④ $\cfrac{1-\sqrt{5}}{2}$
⑤ $\cfrac{-1+\sqrt{5}}{2}$ ⑥ $\cfrac{-1-\sqrt{5}}{2}$
⑦ $-\cfrac{1}{2}$ ⑧ $\cfrac{-1+\sqrt{5}}{2}$
⑨ $\cfrac{-1-\sqrt{5}}{2}$
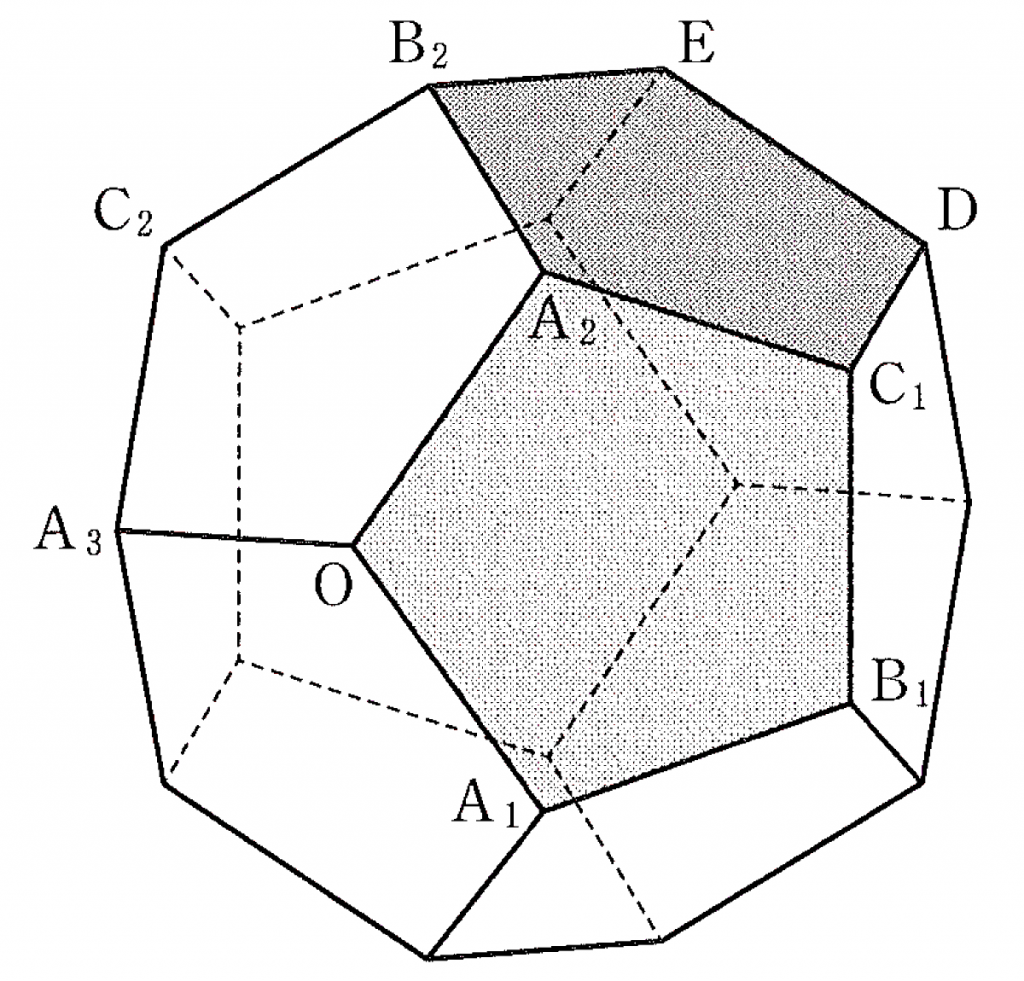
最後に,面 $\text{A}_2\text C_1\text {DEB}_2$ に着目する。
$\overrightarrow{\text{B}_2\text{D}}=\boxed{\text ウ}\space\overrightarrow{\text{A}_2\text{C}_1}=\overrightarrow{\text{O}\text{B}_1}$
であることに注意すると,4点 $\text O$,$\text B_1$,$\text D$,$\text B_2$ は同一平面上にあり,四角形 $\text{OB}_1\text{DB}_2$ は,$\boxed{\boxed{\sf セ}}$ ことがわかる。
$\boxed{\boxed{\text セ}}$ の解答群
⓪ 正方形である
① 正方形ではないが,長方形である
② 正方形ではないが,ひし形である
③ 長方形でもひし形でもないが,平行四辺形である
④ 平行四辺形ではないが,台形である
⑤ 台形でない
ただし,少なくとも一組の対辺が平行な四角形を台形という。
SNSでシェア