【スマホで読む・わかりやすい】共通テスト数学IIB2021本試【解説・正解・問題】
第2問 正解
ア 3 イ,ウ 2,3 エ 4 オ c
カ,キ b,c クケ,コ -c,b
サ,シ,ス 3,3,3 セ 0 ソ 5
タ,チ 3,5 ツ d テ,ト c,d
ナ 2 ニヌ,ネ,ノ -b,a,0
ハヒフ,ヘホ -2b,3a
(1)
$y=3x^2+2x+3$ ・・・・・・①
$y=2x^2+2x+3$ ・・・・・・②
①に $x=0$ を代入すると $y=3$
②に $x=0$ を代入すると $y=3$
となり,どちらも $y$ 軸との交点の $y$ 座標は $3$ である。
・・・ア
①を微分すると
$y’=6x+2$
$x=0$ とすると $y’=2$ となるので,接線の傾きは $2$ である。
②を微分すると
$y’=4x+2$
$x=0$ とすると $y’=2$ となるので,接線の傾きは $2$ である。
どちらも,$y$ 軸との交点における接線の傾きは $2$ であり,かつ $(0,3)$ を通るので,接線の方程式は
$y-3=2(x-0)$
$y=2x+3$
・・・イウ
次に,選択肢のうち,$y$ 軸との交点における接線の方程式が $y=2x+3$ となるものを選ぶ。
⓪ $y=3x^2-2x-3$
① $y=-3x^2+2x-3$
② $y=2x^2+2x-3$
③ $y=2x^2-2x+3$
④ $y=-x^2+2x+3$
⑤ $y=-x^2-2x+3$
これらのうち,$(0,3)$ を通るものは,③,④,⑤
それぞれ微分すると,③は
$y’=4x-2$
$x=0$ とすると $y’=-2$ となり,接線の傾きは一致しない。
④は
$y’=-2x+2$
$x=0$ とすると $y’=2$ となり,接線の傾きは一致する。
$y=-x^2+2x+3$ に $x=0$ を代入すると $y=3$ となる。よって,接線の方程式は $y=2x+3$ となる。
⑤は
$y’=-2x-2$
$x=0$ とすると $y’=-2$ となり,接線の傾きは一致しない。
したがって,④が正しい。
・・・エ
さらに,$y=ax^2+bx+c$ とすると
$x=0$ のとき $y=c$ となるので,曲線は $(0,c)$ を通る。
・・・オ
曲線上の点 $(0,c)$ における接線を $\ell$ とすると,式を微分して
$y’=2ax+b$
$x=0$ のとき $y’=b$ となるので,接線の傾きは $b$ である。接線の式は
$y-c=b(x-0)$
$y=bx+c$
・・・カキ
接線 $\ell$ と $x$ 軸との交点を求めると,$y=0$ として
$0=bx+c$
$bx=-c$
$x=\cfrac{-c}{b}$
・・・クケ,コ
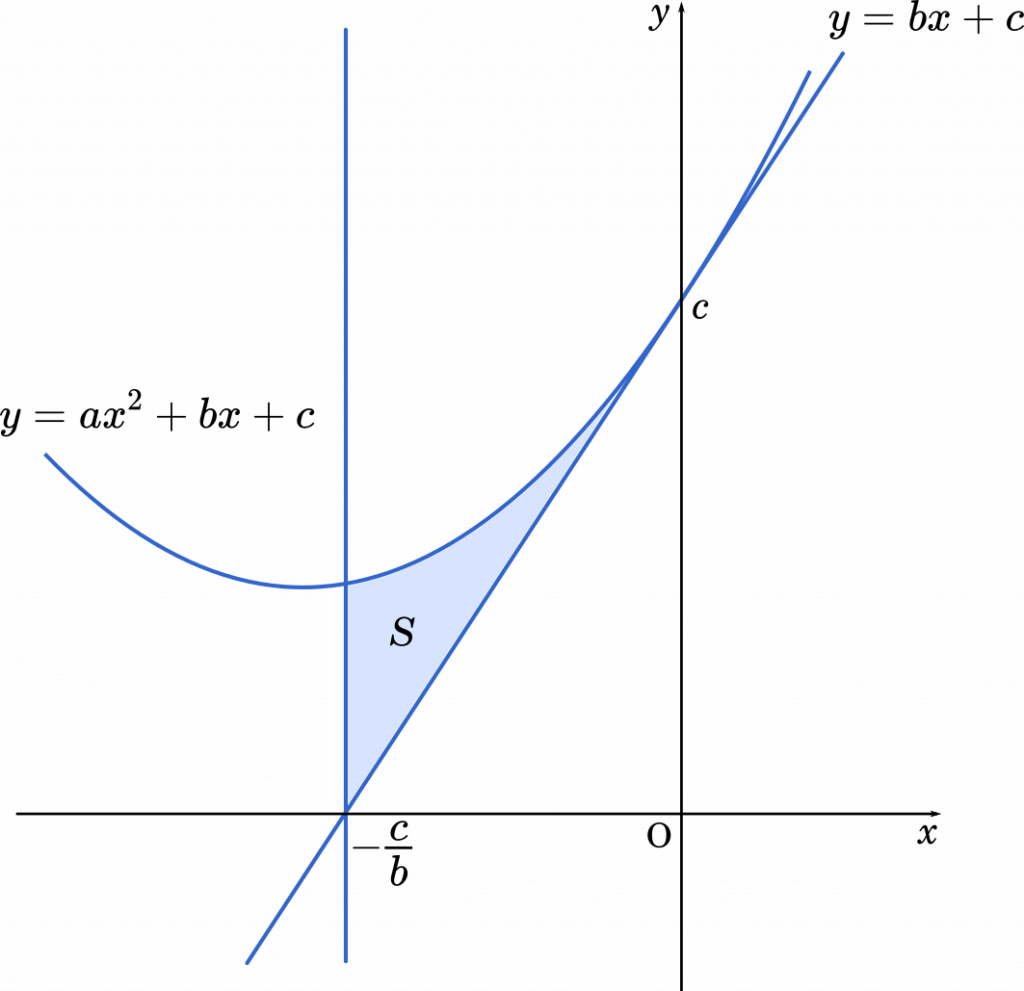
曲線と接線,$x=-\cfrac{c}{b}$ で囲まれた図形の面積 $S$ を求めると
$\displaystyle S=\int_{\small{-\cfrac{c}{b}}}^0 ax^2+bx+c-(bx+c)\space dx$
$\displaystyle =\int_{\small{-\cfrac{c}{b}}}^0 ax^2\space dx$
$\displaystyle =a\int_{\small{-\cfrac{c}{b}}}^0 x^2\space dx$
$=a\Big[\cfrac{x^3}{3}\Big]_{\small{-\cfrac{c}{b}}}^0$
$=\cfrac{a}{3}\Big\{0-\Big(-\cfrac{c}{b}\Big)^3\Big\}$
$=\cfrac{a}{3}\cdot\cfrac{c^3}{b^3}$
$=\cfrac{ac^3}{3b^3}$ ・・・・・・③
・・・サ,シ,ス
$a=1$ として
$S=\cfrac{c^3}{3b^3}$
$c^3=3Sb^3$
$S$ は定数だから,この関数は $b$ の値によって $c$ の値が変化するグラフをつくる。
$S>0$,$b>0$,$c>0$ より
$c=\sqrt[3]{3S}b$
$\sqrt[3]{3S}$ は定数となるので,これは一次関数であり,つまり直線となる。
また,$b=0$ のとき $c=0$ となるので,このグラフは原点を通る。よって⓪が最も適当である。
・・・セ
(2)
$y=4x^3+2x^2+3x+5$ ・・・・・・④
$y=-2x^3+7x^2+3x+5$ ・・・・・・⑤
$y=5x^3-x^2+3x+5$ ・・・・・・⑥
$x=0$ を代入すると,いずれも $y=5$ である。したがって,$y$ 軸との交点の $y$ 座標は $5$ である。
・・・ソ
接線の方程式を求めると,それぞれ微分して
$y’=12x^2+4x+3$
$y’=-6x^2+14x+3$
$y’=15x^2-2x+3$
$x=0$ を代入すると,いずれも $y’=3$ となる。つまり接線の傾きは $3$ である。
これが点 $(0,5)$ を通るので,接線の方程式は
$y-5=3(x-0)$
$y=3x+5$
・・・タ,チ
$y=ax^3+bx^2+cx+d$ に $x=0$ を代入すると,$y=d$ となるので,点 $(0,d)$ を通る。
・・・ツ
式を微分すると
$y’=3ax^2+2bx+c$
$x=0$ のとき $y’=c$ だから,接線の傾きは $c$ である。これが点 $(0,d)$ を通るので,接線の方程式を求めると
$y-d=c(x-0)$
$y=cx+d$
・・・テ,ト
次に
$f(x)=ax^3+bx^2+cx+d$
$g(x)=cx+d$
として
$h(x)=f(x)-g(x)$
とおく。
$h(x)=ax^3+bx^2+cx+d-(cx+d)$
$=ax^3+bx^2$
$y=h(x)$ としてグラフの概形を考えると,$x=0$ のとき
$y=h(0)=0$
となるので,グラフは原点を通る。
また,$h(x)$ を微分して
$y’=3ax^2+2bx$
$3ax^2+2bx=0$ とすると
$x(3ax+2b)=0$
$x=0,-\cfrac{2b}{3a}$
解の大小関係を考えると
$a>0$,$b>0$ だから
$-\cfrac{2b}{3a}<0$
増減表は
$\def\arraystretch{1.25}\begin{array}{|c||c|c|c|c|c|}\hline x&\cdots&-\frac{2b}{3a}&\cdots&0&\cdots\\\hline y’&+&0&-&0&+\\\hline y&\nearrow&\sf{極大}&\searrow&\sf{極小}&\nearrow\\\hline\end{array}$
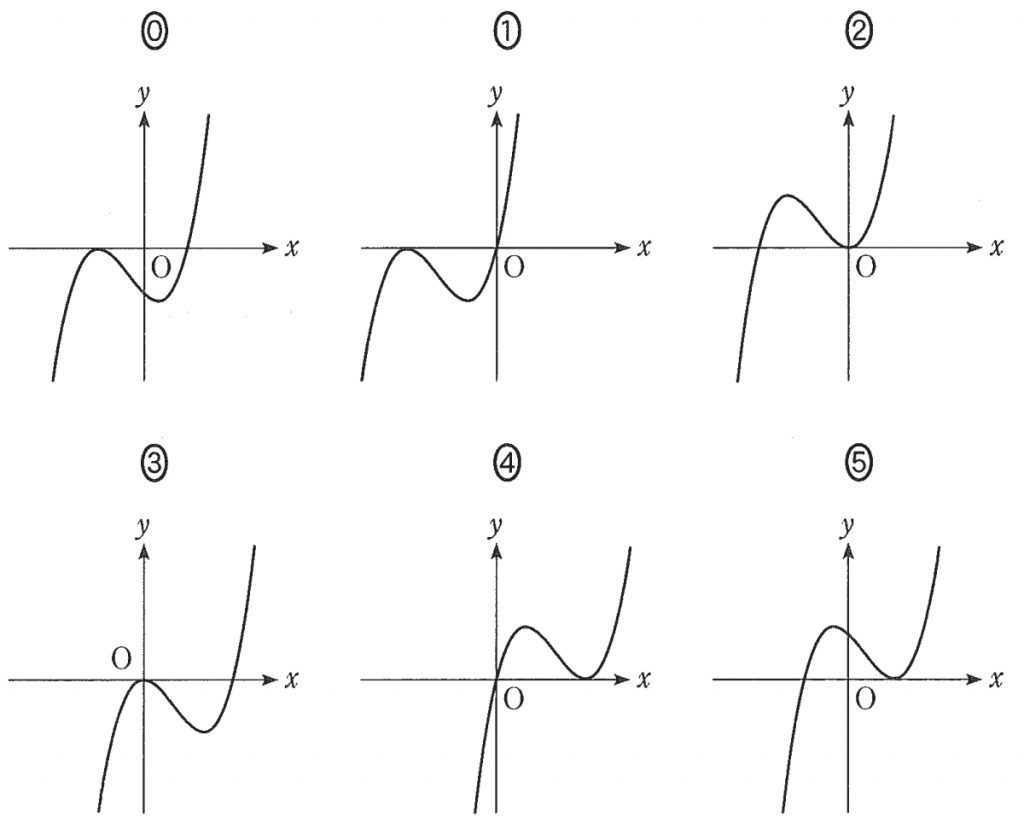
したがって,グラフは原点で極小値をとるので,②が最も適当である。
・・・ナ
$f(x)$ と $g(x)$ の共有点を求めると
$f(x)=g(x)$
$f(x)-g(x)=0$
$h(x)=0$
$ax^3+bx^2=0$
$x^2(ax+b)=0$
$x=0,\cfrac{-b}{a}$
・・・・ニヌ,ネ,ノ
また
$|f(x)-g(x)|=|h(x)|$
とすると
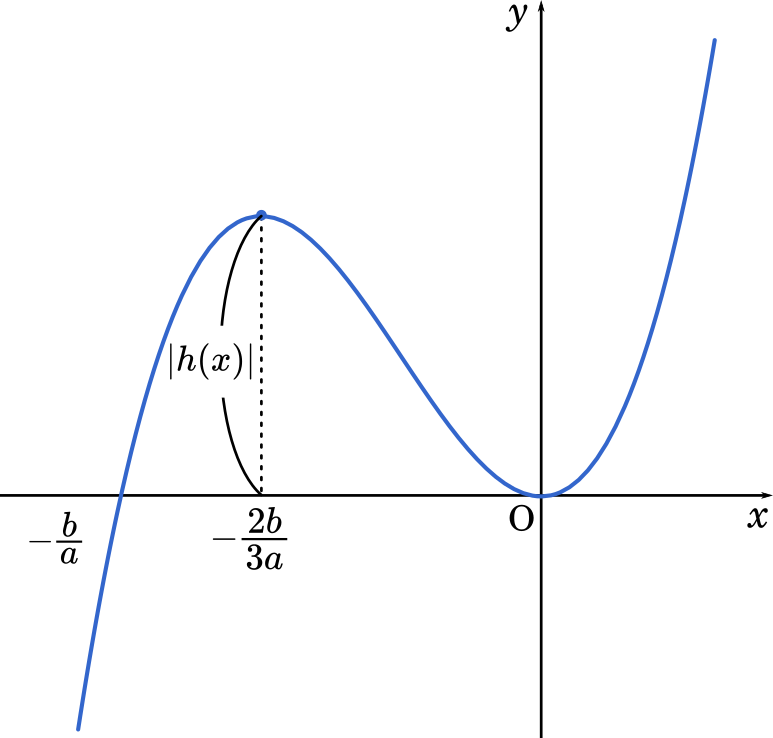
グラフの概形を利用して,$-\cfrac{b}{a}\leqq x\leqq0$ の範囲で $|h(x)|$ が最大となるのは,グラフの極大値,つまり $x=\cfrac{-2b}{3a}$ のときである。
・・・ハヒフ,ヘホ
問題文
第2問
(1) 座標平面上で,次の二つの2次関数のグラフについて考える。
$y=3x^2+2x+3$ ・・・・・・①
$y=2x^2+2x+3$ ・・・・・・②
①,②の2次関数のグラフには次の共通点がある。
共通点
・$y$ 軸との交点の$y$座標は,$\boxed{\sf ア}$ である。
・$y$ 軸との交点における接線の方程式は $y=\boxed{\sf イ}x+\boxed{\sf ウ}$ である。
次の①~⑤の2次関数のグラフのうち,$y$ 軸との交点における接線の方程式が $y=\boxed{\text イ}x+\boxed{\text ウ}$ となるものは $\boxed{\boxed{\sf エ}}$ である。
$\boxed{\boxed{\text エ}}$ の解答群
⓪ $y=3x^2-2x-3$
① $y=-3x^2+2x-3$
② $y=2x^2+2x-3$
③ $y=2x^2-2x+3$
④ $y=-x^2+2x+3$
⑤ $y=-x^2-2x+3$
$a$,$b$,$c$ を $0$ でない実数とする。
曲線 $y=ax^2+bx+c$ 上の点 $(0,\boxed{\sf オ})$ における接線を $\ell$ とすると,その方程式は $y=\boxed{\sf カ}x+\boxed{\sf キ}$ である。
接線 $\ell$ と $x$ 軸との交点の $x$ 座標は $\cfrac{\boxed{\sf クケ}}{\boxed{\sf コ}}$ である。
$a$,$b$,$c$ が正の実数であるとき,曲線 $y=ax^2+bx+c$ と接線 $\ell$ および直線 $\cfrac{\boxed{\text クケ}}{\boxed{\text コ}}$ で囲まれた図形の面積を $S$ とすると
$S=\cfrac{ac^{\boxed{\sf サ}}}{\boxed{\sf シ}\enspace b^{\boxed{\sf ス}}}$ ・・・・・・③
である。
③において,$a=1$ とし,$S$ の値が一定となるように正の実数 $b$,$c$ の値を変化させる。このとき,$b$ と $c$ の関係を表すグラフの概形は $\boxed{\boxed{\sf セ}}$ ある。
$\boxed{\boxed{\text セ}}$ については,最も適当なものを,次の①~⑤のちから一つ選べ。
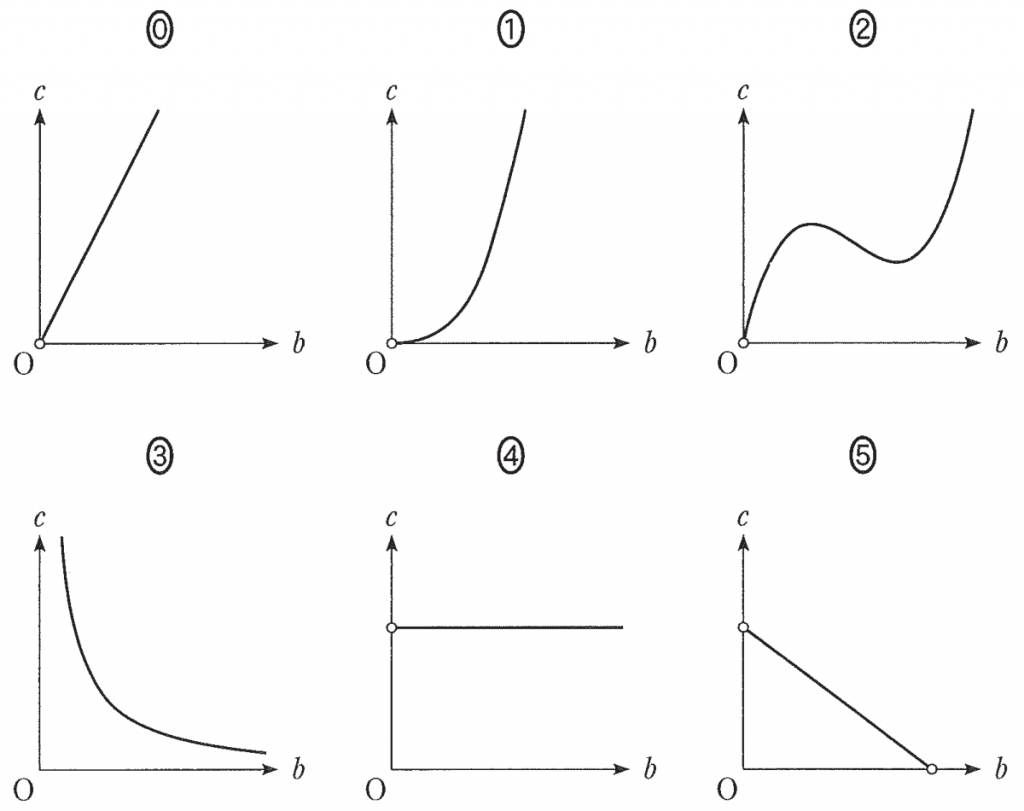
(2) 座標平面上で,次の三つの3次関数のグラフについて考える。
$y=4x^3+2x^2+3x+5$ ・・・・・・④
$y=-2x^3+7x^2+3x+5$ ・・・・・・⑤
$y=5x^3-x^2+3x+5$ ・・・・・・⑥
④,⑤,⑥ の3次関数のグラフには次の共通点がある。
共通点
・$y$ 軸との交点の$y$座標は $\boxed{\sf ソ}$ である。
・$y$ 軸との交点における接線の方程式は $y=\boxed{\sf タ}x+\boxed{\sf チ}$ である。
$a$,$b$,$c$,$d$ を $0$ でない実数とする。
曲線 $y=ax^3+bx^2+cx+d$ 上の点 $(0,\boxed{\sf ツ})$ における接線の方程式は $y=\boxed{\sf テ}x+\boxed{\sf ト}$ である。
次に,$f(x)=ax^3+bx^2+cx+d$,$g(x)=\boxed{\text テ}x+\boxed{\text ト}$ とし,$f(x)-g(x)$ について考える。
$h(x)=f(x)-g(x)$ とおく。$a$,$b$,$c$,$d$ が正の実数であるとき,$y=h(x)$ のグラフの概形は $\boxed{\boxed{\sf ナ}}$ である。
$y=f(x)$ のグラフと $y=g(x)$ のグラフの共有点の $x$ 座標は $\cfrac{\boxed{\sf ニヌ}}{\boxed{\sf ネ}}$ である。また,$x$ が $\cfrac{\boxed{\text ニヌ}}{\boxed{\text ネ}}$ の間を動くとき,$|f(x)-g(x)|$ の値が最大となるのは,$x=\cfrac{\boxed{\sf ハヒフ}}{\boxed{\sf ヘホ}}$ のときである。
$\boxed{\boxed{\text ナ}}$ については,最も適当なものを,次の⓪~⑤のうちから一つ選べ。
SNSでシェア