【スマホで読む・わかりやすい】共通テスト数学IA2021本試【解説・正解・問題】

第5問　正解

ア,イ　3,2　ウ,エ,オ　3,5,2
カ,キ　2,5　ク　5　ケ　5
コ,サ　5,4　シ　1　ス　5
セ,ソ　5,2　タ　1

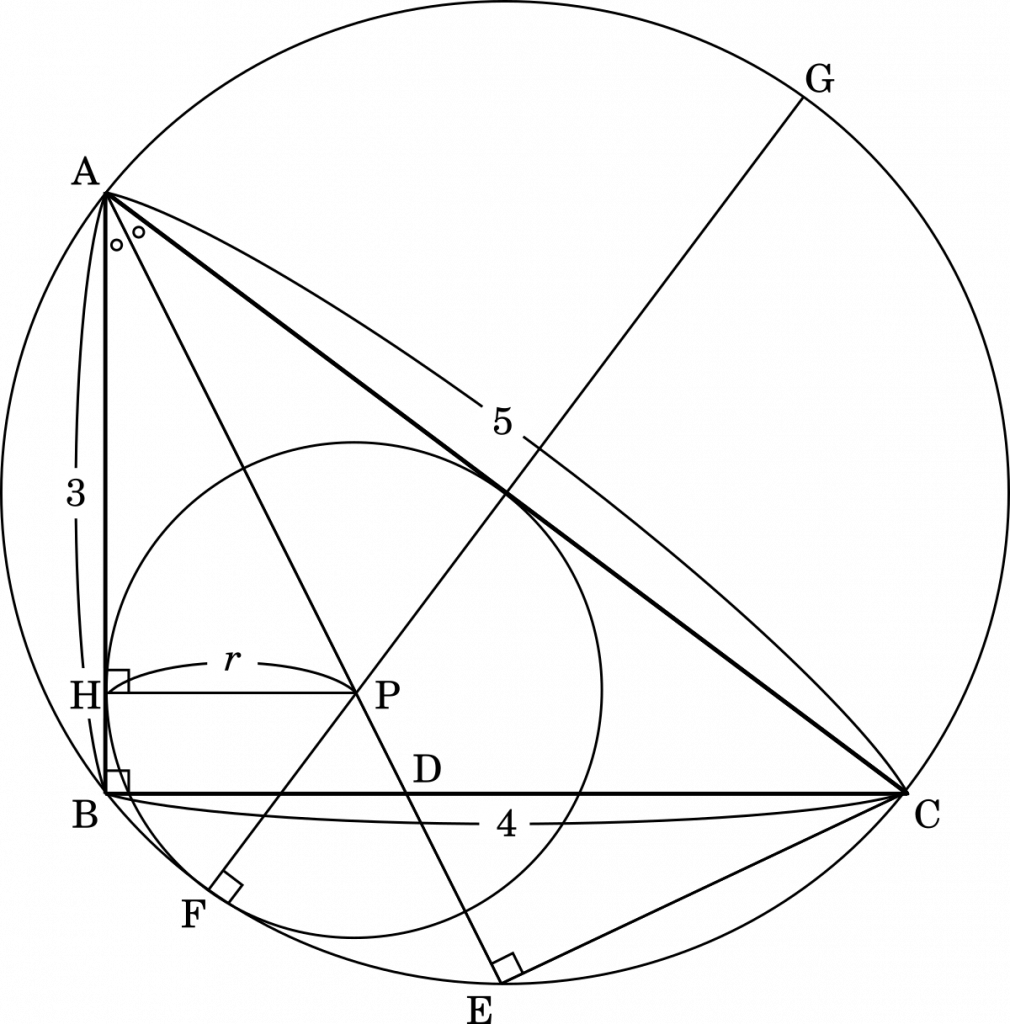
【補足】この問題は，辺の比が $3:4:5$ であることから，△ABCが直角三角形であることを見抜けるかどうかがポイントとなる。もし初めの段階で気づかなかったとしても，BD や AD を求める過程で余弦定理を試して，そのことに気づくと良い。
共通テストは暗記ではなく思考力を重視した試験であるため，仮定と検証のプロセスを実践して，与えられた条件の中から数式や図形の性質を発見する作業を心掛けるべきである。

余弦定理より

$5^2=3^2+4^2-2\times3\times4\times\cos B$
$25=9+16-24\cos B$
$24\cos B=0$
$\cos B=0$

よって，△ABCは $B=90\degree$ の直角三角形である。

BD を求めると

角の二等分線の性質より

AB : AC = BD : CD
BD : CD = $3:5$

したがって

BD = $4\times\cfrac{3}{8}=\cfrac{3}{2}$

・・・・・・アイ

次に，△ABD は直角三角形だから，三平方の定理より

$\text{AD}^2=3^2+\Big(\cfrac{3}{2}\Big)^2$
$=\cfrac{45}{4}$

AD ＞ 0 より

AD = $\cfrac{\sqrt{45}}{2}=\cfrac{3\sqrt{5}}{2}$

・・・・・・ウエオ

さらに，△AEC に着目すると，円周角の定理より

∠ABC = ∠AEC = $90\degree$

よって，△AEC は直角三角形である。

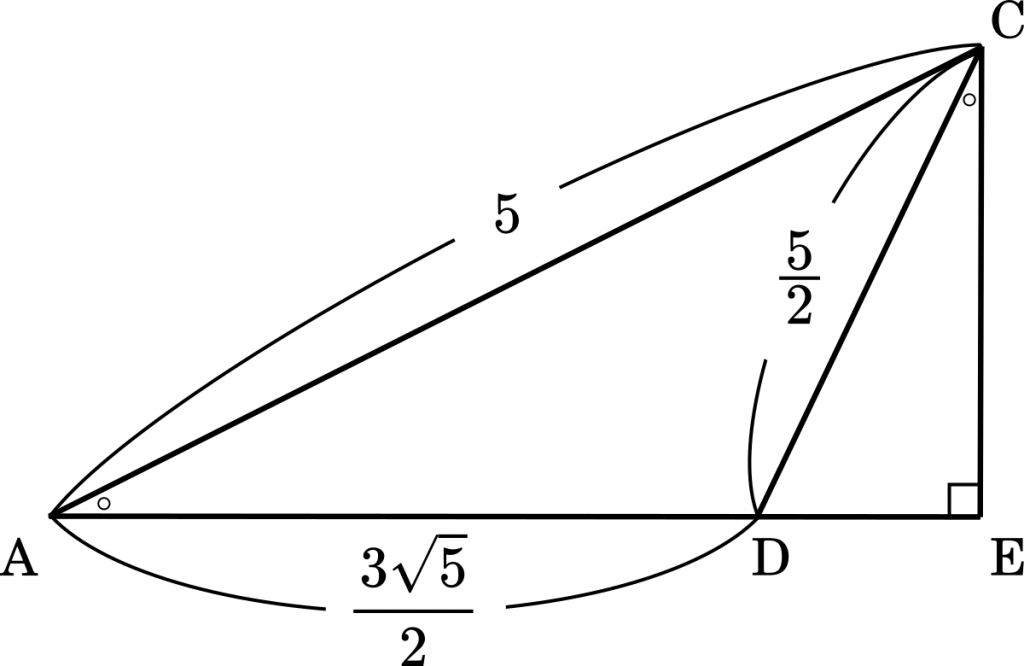
△AEC∽△CDE より

それぞれの辺の比は $5:\cfrac{5}{2}=2:1$

AE : CE = CE : DE
2 : 1 = CE : DE
2 : 1 = $\cfrac{1}{2}$AE : DE
$\cfrac{1}{2}$AE = 2DE
DE = $\cfrac{1}{4}$AE

よって AD : DE = 3 : 1

AE = $\cfrac{4}{3}\times\cfrac{3\sqrt{5}}{2}=2\sqrt{5}$

・・・・・・カキ

次に，AP，PG を考える。

点 P から辺 AB に下ろした垂線との接点を H とすると

△AHP∽△ABD より

AP : HP ＝ AD : BD
AP : $r$ = $\cfrac{3\sqrt{5}}{2}:\cfrac{3}{2}$
$=\sqrt{5}:1$
AP = $\sqrt{5}r$

・・・・・・ク

また，PG = FG – $r$ を考えると

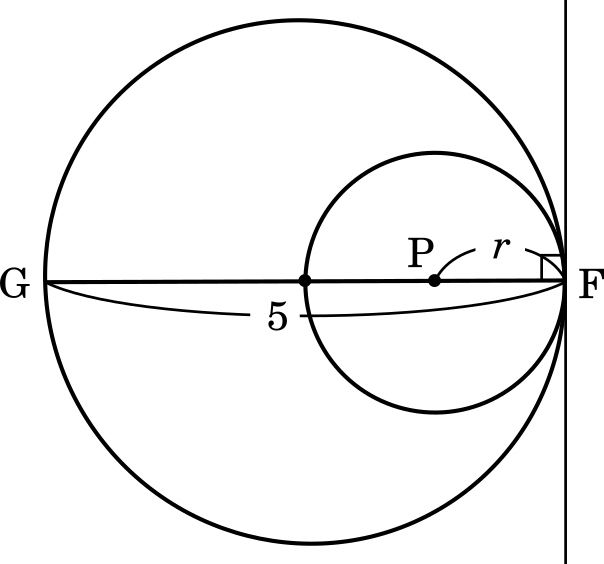
∠ABD = $90\degree$ より，辺 AC は外接円の直径であり，その直径は 5 である。

上の図のように，2 つの円が内接するとき，その接線から引いた垂線はそれぞれの円の中心を通る。

したがって

PG = 5 – $r$

・・・・・・ケ

したがって，方べきの定理より

$\text{PA}\cdot\text{PE}=\text{PG}\cdot\text{PF}$
$\text{PA}\cdot(\text{AE}-\text{AP})=\text{PG}\cdot\text{PF}$
$\sqrt{5}r\cdot(2\sqrt{5}-\sqrt{5}r)=(5-r)\cdot r$
$10r-5r^2=5r-r^2$
$4r^2+5r-10r=0$
$4r^2-5r=0$

$r\not= 0$ より

$4r-5=0$
$r=\cfrac{5}{4}$

・・・・・・コサ

【別解】∠ABC = $90\degree$ より辺 AC は△ABCの外接円の直径である。よって，辺 AC の中点が外接円の中心である。上のように 2 つの円が内接することを考えると，円 P が△ABCの外接円の中心を通ることは明らかだから，$r$ は 5 の 4 等分，すなわち $r=\cfrac{5}{4}$ である。

次に，内接円 Q を考える。

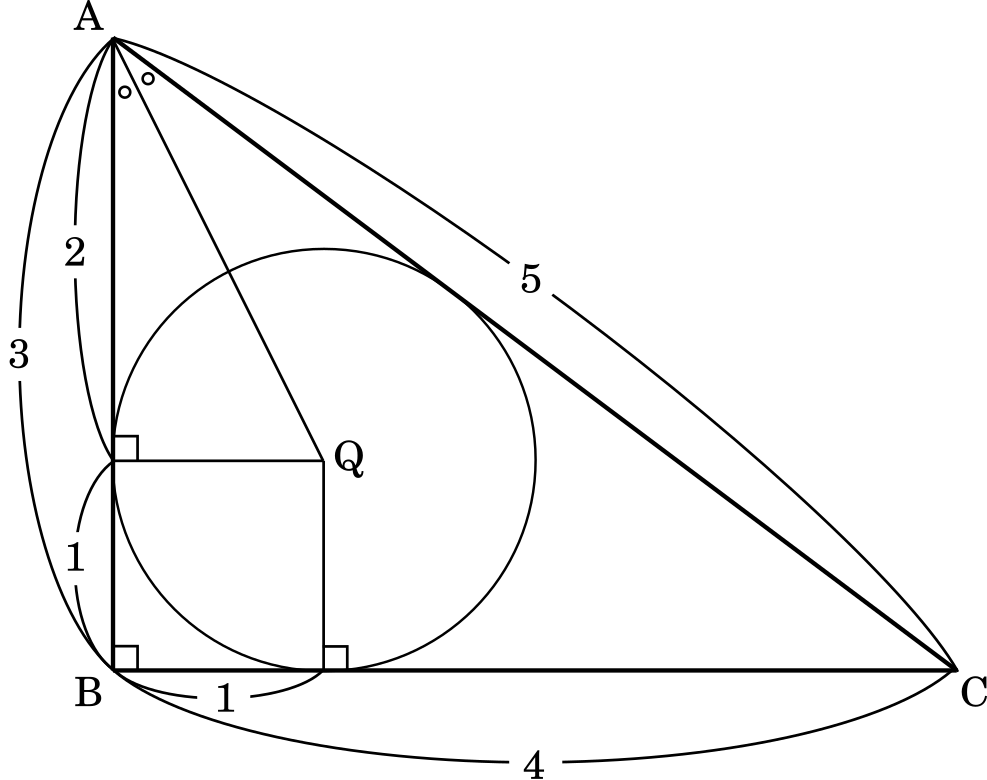
△ABC の面積は $\cfrac{1}{2}\times4\times3=6$ だから

公式 $S=\cfrac{1}{2}r(a+b+c)$ より

$6=\cfrac{1}{2}r(3+4+5)$
$r=1$

・・・・・・シ

三平方の定理より

$\text{AQ}^2=1^2+2^2=5$

AQ ＞ 0 より

$\text{AQ}=\sqrt{5}$

・・・・・・ス

また，円 P と辺 AB との接点を H とすると △ABD∽△AHP が成り立つ。

HP = $r$ = $\cfrac{5}{4}$ だから

BD : HP = $\cfrac{3}{2}:\cfrac{5}{4}$
$=6:5$

△ABD と △AHP の相似比は 6 : 5 である。したがって

$\text{AH}=\text{AB}\times\cfrac{5}{6}$
$=3\times\cfrac{5}{6}=\cfrac{5}{2}$

・・・・・・セソ

4 点が同一円周上にあるかどうかを調べるには，方べきの定理の逆を用いると良い。

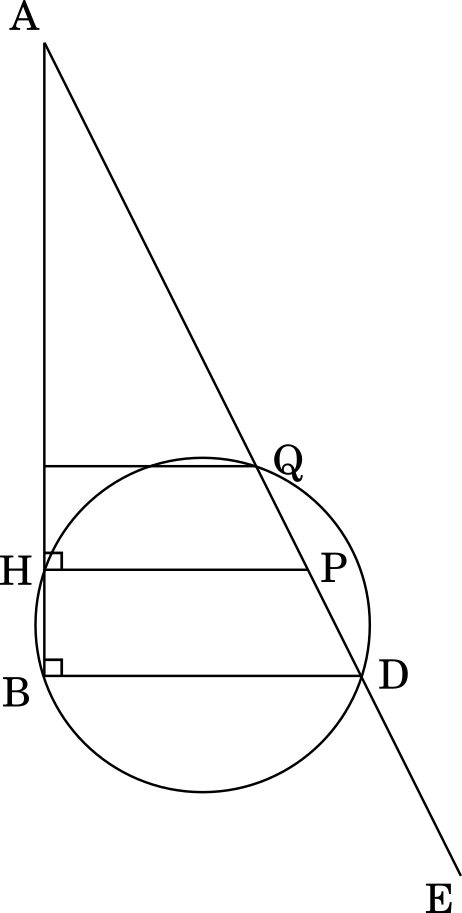
点 H，B，D，Q について，方べきの定理が成り立つと仮定して式を立てると

$\text{AQ}\cdot\text{AD}=\sqrt{5}\times\cfrac{3\sqrt{5}}{2}=\cfrac{15}{2}$
$\text{AH}\cdot\text{AB}=\cfrac{5}{2}\times3=\cfrac{15}{2}$

$\text{AQ}\cdot\text{AD}=\text{AH}\cdot\text{AB}$ が成り立つので，点 H，B，D，Q は同一円周上にある。

したがって，(a)は正。

また，点 H，B，E，Q について，上と同様に

$\text{AQ}\cdot\text{AE}=\sqrt{5}\times2\sqrt{5}=10$

$\text{AQ}\cdot\text{AE}\not=\text{AH}\cdot\text{AB}$ より，点 H，B，E，Q は同一円周上にない。

したがって，(b)は誤。

・・・・・・タ

問題文

第5問

△ABCにおいて，AB = $3$，BC = $4$，AC = $5$ とする。

∠BACの二等分線と辺 BC との交点を D とすると 

BD = $\cfrac{\boxed{\sf ア}}{\boxed{\sf イ}}$，AD = $\cfrac{\boxed{\sf ウ}\sqrt{\boxed{\sf エ}}}{\boxed{\sf オ}}$

である。 

また，∠BAC の二等分線と △ABC の外接円 O との交点で点 A とは異なる点 を E とする。△AEC に着目すると 

AE = $\boxed{\sf カ}\sqrt{\boxed{\sf キ}}$

である。 

△ABC の 2 辺 AB と AC の両方に接し，外接円 O に内接する円の中心を P とする。円 P の半径を $r$ とする。さらに，円 P と外接円 O との接点を F とし，直線 PF と外接円 O との交点で点 F とは異なる点を G とする。このとき

AP = $\sqrt{\boxed{\sf ク}}r$，PG = $\boxed{\sf ケ}-r$

と表せる。したがって，方べきの定理により $r=\cfrac{\boxed{\sf コ}}{\boxed{\sf サ}}$ である。 

△ABC の内心を Q とする。内接円 Q の半径は $\boxed{\sf シ}$ で，AQ = $\sqrt{\boxed{\sf ス}}$ である。また，円 P と辺 AB との接点を H とすると，AH =  $\cfrac{\boxed{\sf セ}}{\boxed{\sf ソ}}$ である。 

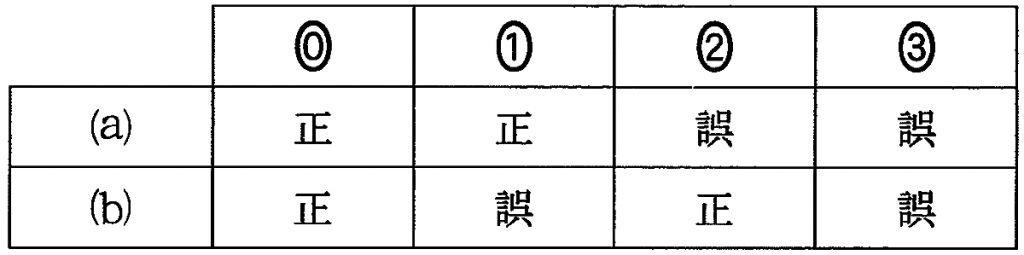
以上から，点 H に関する次の(a)，(b)の正誤の組合せとして正しいものは $\boxed{\boxed{\sf タ}}$ である。

(a)　点 H は 3 点 B，D，Q を通る円の周上にある。
(b)　点 H は 3 点 B，E，Q を通る円の周上にある。

$\boxed{\boxed{タ}}$ の解答群