【スマホで読む・わかりやすい】共通テスト数学IA2021本試【解説・正解・問題】

第1問　正解と解説

ア,イ,ウ 2,5,2　エ,オカ,キ -5,65,4
ク,ケコ,サ 5,65,2　シ 6 ス 3
セ,ソ 4,5　タチ 12　ツテ 12
ト 2　ナ 0　ニ 1　ヌ 3
ネ 2　ノ 2　ハ 0　ヒ 3

〔1〕(1)

$c=1$ のとき

①に $c=1$ を代入して
$2x^2+(4\times1-3)x+2\times1^2-1-11=0$
$2x^2+x-10=0$
$(2x+5)(x-2)=0$

・・・・・・アイウ

$x=-\cfrac{5}{2},\enspace2$

〔1〕(2)

$c=2$ のとき

①に代入して
$2x^2+(4\times2-3)x+2\times2^2-2-11=0$
$2x^2+5x-5=0$

二次方程式の解の公式より
$x=\cfrac{-5\pm\sqrt{25+40}}{4}$
$=\cfrac{-5\pm\sqrt{65}}{4}$

・・・・・・エオカキ

大きい方の解を $\alpha$ とすると
$\alpha=\cfrac{-5+\sqrt{65}}{4}$
両辺の逆数をとると
$\cfrac{1}{\alpha}=\cfrac{4}{-5+\sqrt{65}}$
両辺を 5 倍して
$\cfrac{5}{\alpha}=\cfrac{20}{-5+\sqrt{65}}$
分母を有理化して
$=\cfrac{20(-5-\sqrt{65})}{(-5+\sqrt{65})(-5-\sqrt{65})}$
$=\cfrac{-100-20\sqrt{65}}{25-65}$
$=\cfrac{-100-20\sqrt{65}}{-40}$
$=\cfrac{5+\sqrt{65}}{2}$

・・・・・・クケコサ

まず，$\sqrt{65}$ がどの範囲にあるかを考え，$\cfrac{5+\sqrt{65}}{2}$ に合わせていくと良い。

$64<65<81$
$8^2<65<9^2$
$8<\sqrt{65}<9$
$13<5+\sqrt{65}<14$
$\cfrac{13}{2}<\cfrac{5+\sqrt{65}}{2}<\cfrac{14}{2}$

ここで，$6<\cfrac{13}{2}$ だから
$6<\cfrac{5+\sqrt{65}}{2}<7$
したがって，$m=6$

・・・・・・シ

〔1〕(3)

①の解を，2 次方程式の解の公式を用いて求めると
$x=\cfrac{-(4c-3)\pm\sqrt{D}}{2\times2}$

このとき，$\sqrt{D}$ の部分が $\sqrt{\textsf{(有理数)}^2}$ の形であれば，解はともに有理数となる。$D$ を求めると

$D=(4c-3)^2-4\times2(2c^2-c-11)$
$=16c^2-24c+9-16c^2+8c+88$
$=-16c+97$

問題文より $c$ は正の整数であり，かつ $D$ は正の数でなければならない。

$-16c+97>0$
$16c<97$
$c<6.0625$

よって，$c$ は 1 から 6 の間のいずれかの整数である。

それぞれについて考えると

・$c=1$ のとき，(1)より解は有理数。

・$c=2$ のとき，(2)より解は無理数。

・$c=3$ のとき

$-16c+97=-16\times3+97=49=7^2$
$\sqrt{\textsf{(有理数)}^2}$ の形に当てはまるので，解は有理数。

・$c=4$ のとき

$-16\times4+97=33$
解は無理数。

・$c=5$ のとき

$-16\times5+97=17$
解は無理数。

・$c=6$ のとき

$-16\times6+97=1$
$1$ を $1^2$ として考えると $\sqrt{\textsf{(有理数)}^2}$ の形に当てはまるので，解は有理数。

したがって，①の解が異なる二つの有理数であるような正の整数 $c$ の個数は 3 個。

・・・・・・ス

〔2〕(1)

公式 $\sin^2x+\cos^2x=1$ を用いて
$\sin^2 A+\Big(\cfrac{3}{5}\Big)^2=1$
$\sin^2 A=1-\cfrac{9}{25}=\cfrac{16}{25}$

$\cos A=\cfrac{3}{5}$ より $A$ は鋭角だから
$\sin A=\cfrac{4}{5}$

・・・・・・セソ

△ABCの面積は，公式 $S=\cfrac{1}{2}bc\sin A$ を用いて
△ABC = $\cfrac{1}{2}\times6\times5\times\cfrac{4}{5}$
$=12$

・・・・・・タチ

次に，△AIDの面積を求める。上と同じ公式で求めるなら，∠DAI の大きさを考える必要がある。

$\angle\text{DAI}=360\degree-90\degree-90\degree-A$
$=180\degree-A$

三角比の相互関係 $\sin x=\sin(180\degree-x)$ を用いて
$\sin\angle\text{DAI}=\sin A$

また，辺 AI = $b$，AD = $c$ より，△AID の面積を求める式は △ABC と同じものになる。

したがって　△AID = $12$

・・・・・・ツテ

〔2〕(2)

$S_1-S_2-S_3=a^2-b^2-c^2$

式の形より三平方の定理を利用することを考えると良い。

$A=90\degree$ のとき，三平方の定理より $a^2=b^2+c^2$ が成り立つ。これをもとにして

・$0\degree<A<90\degree$ のとき
$a^2<b^2+c^2$
$a^2-b^2-c^2<0$

したがって，$S_1-S_2-S_3$ は負の値である。

・・・・・・ト

・$A=90\degree$ のとき
$a^2=b^2+c^2$
$a^2-b^2-c^2=0$

したがって，$S_1-S_2-S_3$ は $0$ である。

・・・・・・ナ

・$90\degree<A<180\degree$ のとき
$a^2>b^2+c^2$
$a^2-b^2-c^2>0$

したがって，$S_1-S_2-S_3$ は正の値である。

・・・・・・ニ

〔2〕(3)

(1)より $T_1=$△ABC

次に，$T_2$ も(1)と同様の方法で求められる。

△BEFにおいて
$\sin B=\sin \angle\text{EBF}$ だから
$T_2=\cfrac{1}{2}ac\sin\angle\text{EBF}$
$T_2=\cfrac{1}{2}ac\sin B$
= △ABC

$T_3$ も同様
△CGHにおいて
$\sin C=\sin \angle\text{GCH}$ だから
$T_3=\cfrac{1}{2}ab\sin C$
= △ABC

したがって
$a,b,c$ の値に関係なく，$T_1=T_2=T_3$

・・・・・・ヌ

〔2〕(4)

$0\degree<A<90\degree$ のとき，ID と BC を比べる。

実際の試験の場では，作図より角が大きくなるほど辺の長さが大きくなることを見抜いて ID ＞ BC としてよい。しかしながら，本来は余弦定理の性質を考えるべきである。

△AID において，三角比の相互関係より
$\cos\angle\text{DAI}=\cos(180\degree-A)$
$=-\cos A$

余弦定理 $a^2=b^2+c^2-2bc\cos A$ より
$\text{DI}^2=b^2+c^2-2bc(-\cos A)$
$=b^2+c^2+2bc\cos A$
また △ABC において，余弦定理より
$a^2=b^2+c^2-2bc\cos A$
$A$ は鋭角より $\cos A>0$ だから
ID ＞ BC　が成り立つ。

・・・・・・ネ

次に外接円の半径を考える。正弦定理 $\cfrac{a}{\sin A}=2R$ を考えて式を立てると良い。

$\text{ID}>\text{BC}$，$\angle\text{DAI}=A$ より
$\cfrac{\text{ID}}{\sin A}>\cfrac{\text{BC}}{\sin A}$
(△AIDの外接円の半径)＞(△ABCの外接円の半径)

・・・・・・ノ

また，上と同様にして
(△BEFの外接円の半径)＞(△ABCの外接円の半径)
(△CGHの外接円の半径)＞(△ABCの外接円の半径)
が成り立つ。

したがって
・$0\degree<A<B<C<90\degree$ のとき，外接円の半径が最も小さい三角形は △ABC である。

・・・・・・ハ

次に，$C>90\degree$ のときを考える。

このとき，$\angle\text{CGH}<90\degree$ である。

上と同様，作図より判断するか，余弦定理より，角が大きくなるほど辺の長さが大きくなる性質を用いて
AB ＞ GH

よって
$\cfrac{\text{AB}}{\sin C}>\cfrac{\text{GH}}{\sin C}$
(△ABCの外接円の半径)＞(△CGHの外接円の半径)

△AID と △BEF については上の不等式と同じである。したがって

・$0\degree<A<B<90\degree<C$ のとき，外接円の半径が最も小さい三角形は △CGH である。

・・・・・・ヒ

問題文

第1問

〔1〕$c$ を正の整数とする。$x$ の 2 次方程式

$2x^2+(4c-3)x+2c^2-c-11=0$ ・・・・・・①

について考える。

(1) $c=1$ のとき，①の左辺を因数分解すると

$(\boxed{\sf ア}x+\boxed{\sf イ})(x-\boxed{\sf ウ})$

であるから，①の解は

$x=-\cfrac{\boxed{\rm イ}}{\boxed{\rm ア}}，\boxed{\rm ウ}$

である。

(2) $c=2$ のとき，①の解は

$x=\cfrac{-\boxed{\sf エ}\pm\sqrt{\boxed{\sf オカ}}}{\boxed{\sf キ}}$

であり，大きい方の解を $\alpha$ とすると

$\cfrac{5}{\alpha}=\cfrac{\boxed{\sf ク}+\sqrt{\boxed{\sf ケコ}}}{\boxed{\sf サ}}$

である。また，$m<\cfrac{5}{\alpha}<m+1$ を満たす整数 $m$ は $\boxed{\sf シ}$ である。

(3) 太郎さんと花子さんは，①の解について考察している。

太郎：①の解は $c$ の値によって，ともに有理数である場合もあれば，ともに無理数である場合もあるよね。$c$ がどのような値のときに，解は有理数になるのかな。

花子：2 次方程式の解の公式の根号の中に着目すればいいんじゃないかな。

①の解が異なる二つの有理数であるような正の整数 $c$ の個数は $\boxed{\sf ス}$ 個である。

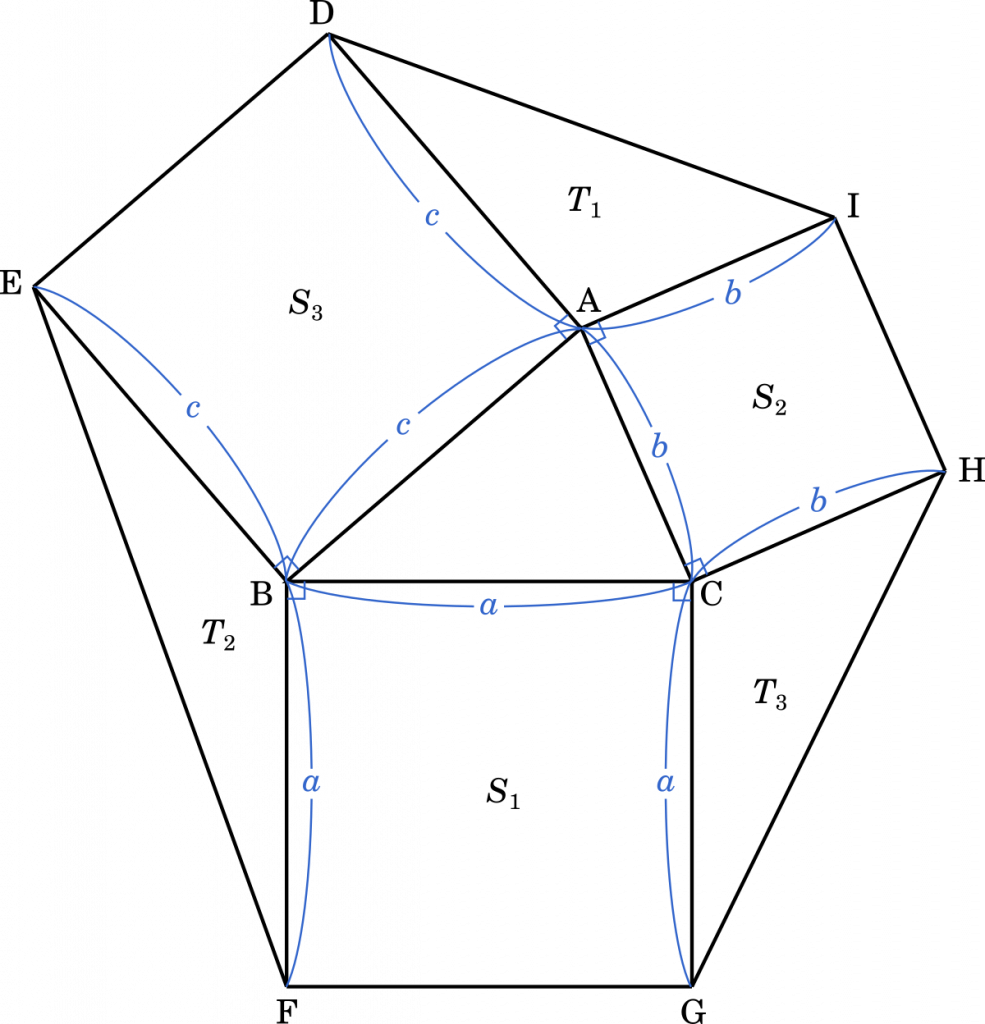
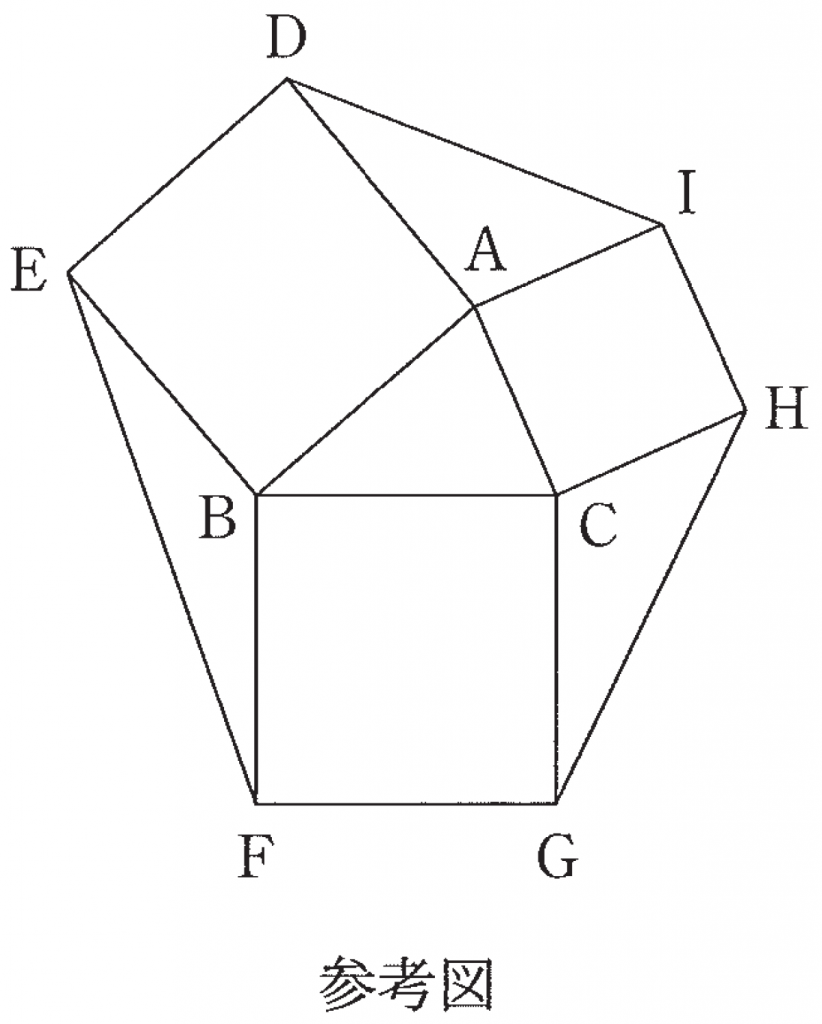
〔2〕右の図のように，△ABCの外側に辺 AB， BC， CA をそれぞれ 1 辺とする正方形 ADEB，BFGC，CHIA をかき，2 点 E と F，G と H，I と D をそれぞれ線分で結んだ図形を考える。以下において

$\text{BC}=a$，$\text{CA}=b$，$\text{AB}=c$
$\angle\text{CAB}=A$，$\angle\text{ABC}=B$，$\angle\text{BCA}=C$

とする。 

(1) $b=6$，$c=5$，$\cos A=\cfrac{3}{5}$ のとき，$\sin A=\cfrac{\boxed{\sf セ}}{\boxed{\sf ソ}}$ であり，△ABC の面積は $\boxed{\sf タチ}$，△AID の面積は $\boxed{\sf ツテ}$ である。

(2) 正方形 BFGC，CHIA，ADEB の面積をそれぞれ $S_1$，$S_2$，$S_3$ とする。このとき，$S_1-S_2-S_3$ は

・$0\degree<A<90\degree$ のとき，$\boxed{\boxed{\sf ト}}$ 。

・$A=90\degree$ のとき，$\boxed{\boxed{\sf ナ}}$ 。

・$90\degree<A<180\degree$ のとき，$\boxed{\boxed{ニ}}$ 。

$\boxed{\boxed{\text{ト}}}$ ～ $\boxed{\boxed{\text{ニ}}}$ の解答群（同じものを繰り返し選んでもよい。）

⓪　$0$ である
①　正の値である
②　負の値である
③　正の値も負の値もとる 

(3) △AID，△BEF，△CGH の面積をそれぞれ $T_1$，$T_2$，$T_3$ とする。このとき，$\boxed{\boxed{\sf ヌ}}$ である。

$\boxed{\boxed{\text{ヌ}}}$ の解答群

⓪　$a<b<c$ ならば，$T_1>T_2>T_3$
①　$a<b<c$ ならば，$T_1<T_2<T_3$
②　$A$ が鈍角ならば，$T_1<T_2$ かつ $T_1<T_3$
③　$a，b，c$ の値に関係なく，$T_1=T_2=T_3$ 

(4) △ABC，△AID，△BEF，△CGH のうち，外接円の半径が最も小さいものを求める。

$0\degree<A<90\degree$ のとき，ID $\boxed{\boxed{\sf ネ}}$ BCであり

(△AID の外接円の半径) $\boxed{\boxed{\sf ノ}}$ (△ABC の外接円の半径) 

であるから，外接円の半径が最も小さい三角形は

・$0\degree<A<B<C<90\degree$ のとき， $\boxed{\boxed{\sf ハ}}$ である。

・$0\degree<A<B<90\degree<C$ のとき，$\boxed{\boxed{\sf ヒ}}$ である。

$\boxed{\boxed{\text{ネ}}}$，$\boxed{\boxed{\text{ノ}}}$ の解答群(同じものを繰り返し選んでもよい。) 

⓪ $<$　① $=$　② $>$

$\boxed{\boxed{\text{ハ}}}$，$\boxed{\boxed{\text{ヒ}}}$ の解答群(同じものを繰り返し選んでもよい。)

⓪　△ABC　①　△AID　②　△BEF　③　△CGH