空間ベクトルと四面体：直角二等辺三角形を利用する(横浜国立大2020文系第1問)

空間内に 4 点 O，A，B，C があり，

$|\overrightarrow{\text{OA}}|=|\overrightarrow{\text{OB}}|=|\overrightarrow{\text{OC}}|=1$
$\overrightarrow{\text{OA}}\cdot\overrightarrow{\text{OB}}=\overrightarrow{\text{OB}}\cdot\overrightarrow{\text{OC}}=\overrightarrow{\text{OC}}\cdot\overrightarrow{\text{OA}}=k$ $(0<k<1)$

をみたしている。ただし，$\overrightarrow{\text{OA}}\cdot\overrightarrow{\text{OB}}$ は $\overrightarrow{\text{OA}}$ と $\overrightarrow{\text{OB}}$ の内積を表す。三角形 ABC の重心を M とする。線分 OM 上に点 P があり，∠APB = 90° をみたしている。

$\cfrac{|\overrightarrow{\text{OP}}|}{|\overrightarrow{\text{OM}}|}$ と $|\overrightarrow{\text{AP}}|$ をそれぞれ $k$ の式で表せ。

直角三角形を調べる

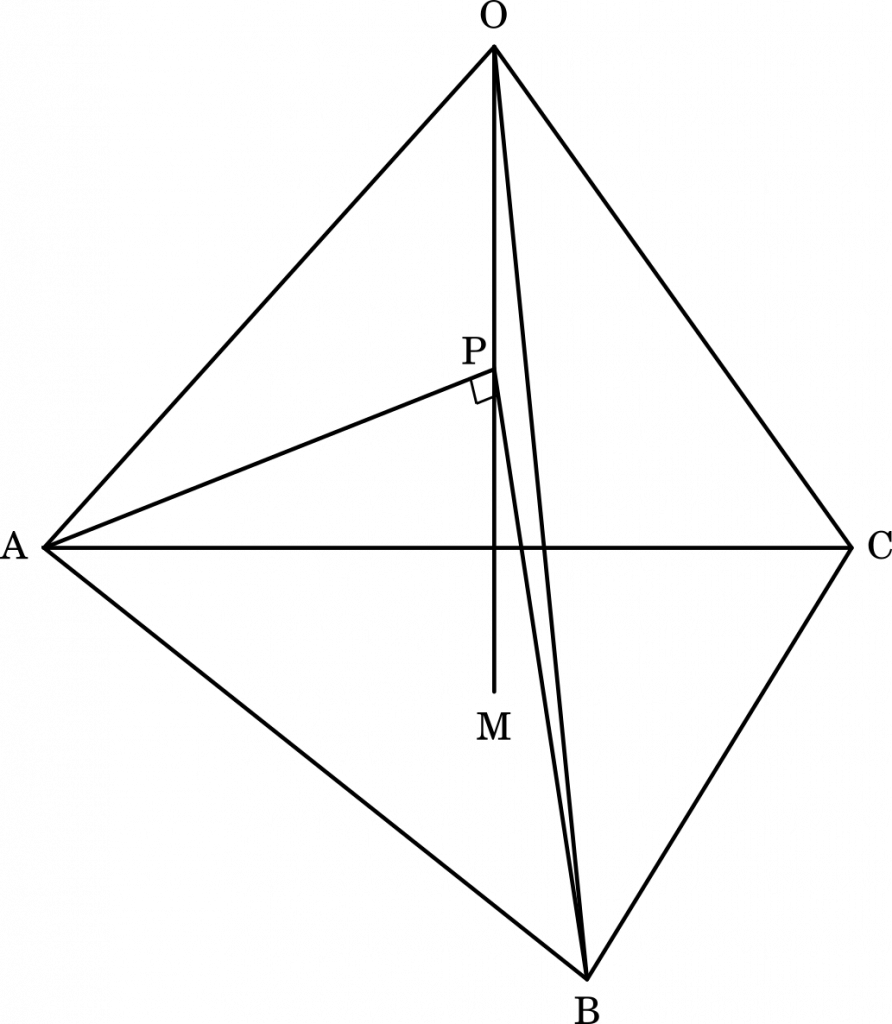
他に手がかりがないかを考えます。△APBは直角三角形です。これについてもう少し掘り下げてみましょう。

そもそも，内積がすべて $k$ であることから，△ABC のそれぞれの辺はすべて等しくなり，正三角形であると言えます。よって，AP と BP は同じ長さなのではないかという推測ができます。

△APB について
$\overrightarrow{\text{AP}}=\overrightarrow{\text{OP}}-\overrightarrow{\text{OA}}$
$|\overrightarrow{\text{AP}}|^2=(\overrightarrow{\text{OP}}-\overrightarrow{\text{OA}})^2$
$|\overrightarrow{\text{AP}}|^2=|\overrightarrow{\text{OP}}|^2-2\overrightarrow{\text{OP}}\cdot\overrightarrow{\text{OA}}+|\overrightarrow{\text{OA}}|^2$　・・・①

同様にして

$|\overrightarrow{\text{BP}}|^2=|\overrightarrow{\text{OP}}|^2-2\overrightarrow{\text{OP}}\cdot\overrightarrow{\text{OB}}+|\overrightarrow{\text{OB}}|^2$　・・・②

ここで，$\overrightarrow{\text{OP}}=t\overrightarrow{\text{OM}}$ とすると，M は △ABC の重心だから
$\overrightarrow{\text{OP}}=\cfrac{t}{3}(\overrightarrow{\text{OA}}+\overrightarrow{\text{OB}}+\overrightarrow{\text{OC}})$

よって

$\overrightarrow{\text{OP}}\cdot\overrightarrow{\text{OA}}=\cfrac{t}{3}(|\overrightarrow{\text{OA}}|^2+\overrightarrow{\text{OA}}\cdot\overrightarrow{\text{OB}}+\overrightarrow{\text{OA}}\cdot\overrightarrow{\text{OC}})$
$=\cfrac{t}{3}(1+2k)$　・・・③

また

$\overrightarrow{\text{OP}}\cdot\overrightarrow{\text{OB}}=\cfrac{t}{3}(\overrightarrow{\text{OA}}\cdot\overrightarrow{\text{OB}}+|\overrightarrow{\text{OB}}|^2+\overrightarrow{\text{OB}}\cdot\overrightarrow{\text{OC}})$
$=\cfrac{t}{3}(1+2k)$　・・・④

これらを①，②に代入すると

$|\overrightarrow{\text{AP}}|^2=|\overrightarrow{\text{BP}}|^2$
$|\overrightarrow{\text{AP}}|=|\overrightarrow{\text{BP}}|$

よって，△APB は AP＝BP の直角二等辺三角形である。

さらに，AB の長さを求めると

$\overrightarrow{\text{AB}}=\overrightarrow{\text{OB}}-\overrightarrow{\text{OA}}$

$|\overrightarrow{\text{AB}}|^2=(\overrightarrow{\text{OB}}-\overrightarrow{\text{OA}})^2$
$=|\overrightarrow{\text{OB}}|^2-2\overrightarrow{\text{OA}}\cdot\overrightarrow{\text{OB}}+|\overrightarrow{\text{OA}}|^2$
$=2-2k$

$|\overrightarrow{\text{AB}}|=\sqrt{2-2k}$

AP : BP : AB ＝ $1:1:\sqrt{2}$ だから

$|\overrightarrow{\text{AP}}|=|\overrightarrow{\text{AB}}|=\cfrac{\sqrt{2-2k}}{\sqrt{2}}$
$=\sqrt{1-k}$　（答え）

t の値を求める

いったん，$\overrightarrow{\text{OP}}=t\overrightarrow{\text{OM}}$ としたので，結局 $\cfrac{|\overrightarrow{\text{OP}}|}{|\overrightarrow{\text{OM}}|}=t$ です。

$t$ の値を求めていきましょう。

とりあえず，まだ内積 0 の関係を使っていないので，式にしてみましょう。

$\overrightarrow{\text{AP}}\cdot\overrightarrow{\text{BP}}=(\overrightarrow{\text{OP}}-\overrightarrow{\text{OA}})(\overrightarrow{\text{OP}}-\overrightarrow{\text{OB}})$
$=|\overrightarrow{\text{OP}}|^2-\overrightarrow{\text{OP}}\cdot\overrightarrow{\text{OB}}-\overrightarrow{\text{OP}}\cdot\overrightarrow{\text{OA}}+\overrightarrow{\text{OA}}\cdot\overrightarrow{\text{OB}}$

③，④より

$=|\overrightarrow{\text{OP}}|^2-\cfrac{2}{3}t(1+2k)+k=0$　・・・⑤

こうなると $|\overrightarrow{\text{OP}}|$ を求める必要が出てきます。

$|\overrightarrow{\text{OP}}|^2=\Big\{\cfrac{t}{3}(\overrightarrow{\text{OA}}+\overrightarrow{\text{OB}}+\overrightarrow{\text{OC}})\Big\}^2$

$=\cfrac{t^2}{9}(|\overrightarrow{\text{OA}}|^2+|\overrightarrow{\text{OB}}|^2+|\overrightarrow{\text{OC}}|^2+2\overrightarrow{\text{OA}}\cdot\overrightarrow{\text{OB}}+2\overrightarrow{\text{OB}}\cdot\overrightarrow{\text{OC}}+2\overrightarrow{\text{OC}}\cdot\overrightarrow{\text{OA}})$
$=\cfrac{t^2}{9}(3+6k)$
$=\cfrac{t^2}{3}(1+2k)$

⑤に代入して

$\cfrac{1}{3}(1+2k)t^2-\cfrac{2}{3}(1+2k)t+k=0$
$(1+2k)t^2-2(1+2k)t+3k=0$
$t=\cfrac{1+2k\pm\sqrt{(1+2k)^2-3k(1+2k)}}{1+2k}$
$=\cfrac{1+2k\pm\sqrt{(1+2k)(1+2k-3k)}}{1+2k}$
$=\cfrac{1+2k\pm\sqrt{(1+2k)(1-k)}}{1+2k}$
$=1\pm\sqrt{\cfrac{(1+2k)(1-k)}{(1+2k)^2}}$
$=1\pm\sqrt{\cfrac{1-k}{1+2k}}$

$0\leqq t\leqq1$ より

$ \cfrac{|\overrightarrow{\text{OP}}|}{|\overrightarrow{\text{OM}}|} =1-\sqrt{\cfrac{1-k}{1+2k}}$　（答え）