空間ベクトル・平面と直線の交点の求めかた(横浜国立大2019理系第2問(文系第2問))

1 辺の長さが 1 である正四面体 OABC がある。辺 OA 上に点 D，辺 OB 上に点 E，辺 OC 上に点 F があり，

OD：DA ＝ 1：1，OE：EB ＝ 2：1，OF：FC ＝ 2：3

をみたしている。さらに辺 OB と辺 AC の中点をそれぞれ M，N とする。平面 DEF と直線 MN の交点を P とする。ベクトル $\overrightarrow{\text{OA}}$，$\overrightarrow{\text{OB}}$，$\overrightarrow{\text{OC}}$ を $\vec{a}$，$\vec{b}$，$\vec{c}$ とおく。次の問いに答えよ。

(1) $|\overrightarrow{\text{MN}}|$ を求めよ。

(2) $\overrightarrow{\text{OP}}$ を $\vec{a}$，$\vec{b}$，$\vec{c}$ を用いて表せ。

(3) $|\overrightarrow{\text{MP}}|$ を求めよ。

絶対値の 2 乗を求める

(1)から始めます。

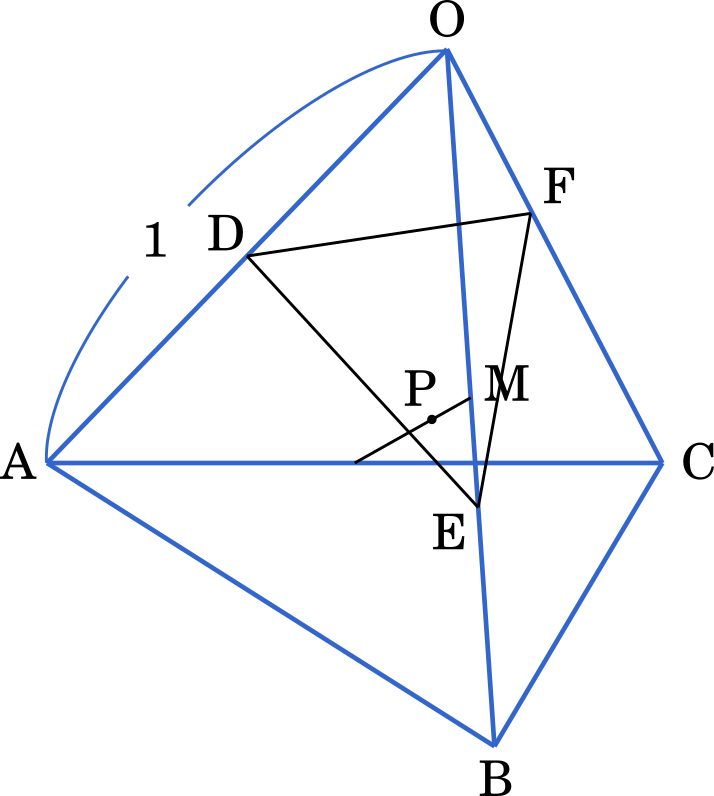
とりあえず $\overrightarrow{\text{MN}}$ を表してみます。

$\overrightarrow{\text{MN}}=\overrightarrow{\text{ON}}-\overrightarrow{\text{OM}}$
$=\cfrac{1}{2}(\vec{a}+\vec{c})-\cfrac{1}{2}\vec{b}$
$=\cfrac{1}{2}(\vec{a}+\vec{c}-\vec{b})$

$|\overrightarrow{\text{MN}}|^2=\cfrac{1}{4}(\vec{a}+\vec{c}-\vec{b})^2$

ここは公式を使いましょう。

$=\cfrac{1}{4}(|\vec{a}|^2+|\vec{c}|^2+|\vec{b}|^2+2\vec{a}\cdot\vec{c}-2\vec{c}\cdot\vec{b}-2\vec{b}\cdot\vec{a})$

△OAC は正三角形だから

$\vec{a}\cdot\vec{c}=|\vec{a}||\vec{c}|\cos60\degree$
$=1\cdot1\cdot\cfrac{1}{2}=\cfrac{1}{2}$

同様にして

$\vec{a}\cdot\vec{b}=\cfrac{1}{2}$
$\vec{b}\cdot\vec{c}=\cfrac{1}{2}$

これらを代入すると

$=\cfrac{1}{4}(1+1+1+1-1-1)$
$=\cfrac{1}{2}$

したがって

$|\overrightarrow{\text{MN}}|=\sqrt{\cfrac{1}{2}}=\cfrac{\sqrt{2}}{2}$　（答え）

平面と直線の交点

(2)に進みます。

平面と直線の交点を求めます。

$\overrightarrow{\text{OP}}=s\overrightarrow{\text{OD}}+t\overrightarrow{\text{OE}}+u\overrightarrow{\text{OF}}$　$(s+t+u=1)$
とする。

空間ベクトルでこの法則が成り立つことは，教科書の証明を読んでもあまりピンと来ない話かもしれません。ここではイメージだけ示しておきます。

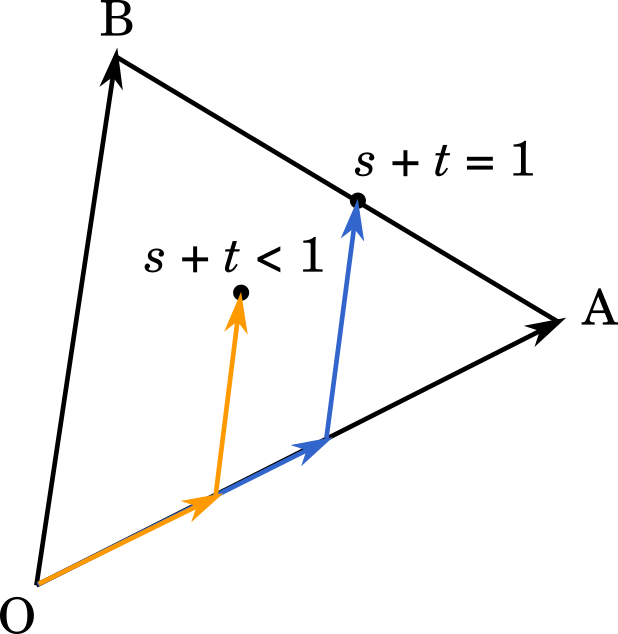
平面ベクトルを学習したとき，ベクトルを $s\overrightarrow{\text{OA}}+t\overrightarrow{\text{OB}}$ とすると，$s+t=1$ のとき，このベクトルは直線 AB 上のどこかを表すと習いました。また，$s+t<1$ のときには，原点 O を出発したベクトルは直線 AB まで届かず，その手前に到着します。

この直線 AB を広げて空間上の平面として考えると，$s+t+u=1$ のときにベクトルはその平面に達することになるのです。また，平面ベクトルで $s+t$ が 1 でないときに直線と違う点に達するのと同じように，$s+t+u$ が 1 でないときには平面ではない点に達するとも言えます。

よって

$\overrightarrow{\text{OP}}=\cfrac{1}{2}s\vec{a}+\cfrac{2}{3}t\vec{b}+\cfrac{2}{5}u\vec{c}$　・・・①

$\overrightarrow{\text{OP}}$ をもう一つ，別の方法で表してみましょう。$\overrightarrow{\text{OP}}$ は $\overrightarrow{\text{MN}}$ の延長線上にあるので，これをベクトル方程式として表してみます。

$\overrightarrow{\text{OP}}=\overrightarrow{\text{OM}}+k\overrightarrow{\text{MN}}$ とすると

$=\cfrac{1}{2}\vec{b}+\cfrac{1}{2}k(\vec{a}+\vec{c}-\vec{b})$
$=\cfrac{1}{2}k\vec{a}+\cfrac{1}{2}(1-k)\vec{b}+\cfrac{1}{2}k\vec{c}$ ・・・②

①，②を比べると

$\begin{cases}\cfrac{1}{2}s=\cfrac{1}{2}k・・・③\\\cfrac{2}{3}t=\cfrac{1}{2}(1-k)・・・④\\\cfrac{2}{5}u=\cfrac{1}{2}k・・・⑤\end{cases}$

連立方程式ができたので，これを解いていきます。

③より

$s=k$

④に代入して

$\cfrac{2}{3}t=\cfrac{1}{2}(1-s)$

$t=\cfrac{3}{4}(1-s)$ ・・・⑥

また，⑤は

$\cfrac{2}{5}u=\cfrac{1}{2}s$
$u=\cfrac{5}{4}s$ ・・・⑦

⑥，⑦を $s+t+u=1$ に代入すると

$s+\cfrac{3}{4}(1-s)+\cfrac{5}{4}s=1$

両辺を 4 倍して

$4s+3-3s+5s=4$
$6s=1$
$s=\cfrac{1}{6}$

⑦に代入して

$t=\cfrac{3}{4}\Big(1-\cfrac{1}{6}\Big)$

$=\cfrac{3}{4}\cdot\cfrac{5}{6}=\cfrac{5}{8}$

⑦に代入して

$u=\cfrac{5}{4}\cdot\cfrac{1}{6}=\cfrac{5}{24}$

したがって

$\overrightarrow{\text{OP}}=\cfrac{1}{2}\cdot\cfrac{1}{6}\vec{a}+\cfrac{2}{3}\cdot\cfrac{5}{8}\vec{b}+\cfrac{2}{5}\cdot\cfrac{5}{24}\vec{c}$
$=\cfrac{1}{12}\vec{a}+\cfrac{5}{12}\vec{b}+\cfrac{1}{12}\vec{c}$　（答え）

再び絶対値の２乗を求める

(3)に進みます。ここも(1)と同様，絶対値を２乗して内積を求めていきます。

$\overrightarrow{\text{MP}}=\overrightarrow{\text{OP}}-\overrightarrow{\text{OM}}$
$=\cfrac{1}{12}\vec{a}+\cfrac{5}{12}\vec{b}+\cfrac{1}{12}\vec{c}-\cfrac{1}{2}\vec{b}$
$=\cfrac{1}{12}(\vec{a}-\vec{b}+\vec{c})$

両辺を２乗して

$|\overrightarrow{\text{MP}}|^2=\cfrac{1}{144}(\vec{a}-\vec{b}+\vec{c})^2$
$=\cfrac{1}{144}(|\vec{a}|^2+|\vec{b}|^2+|\vec{c}|^2-2\vec{a}\cdot\vec{b}-2\vec{b}\cdot\vec{c}+2\vec{c}\cdot\vec{a})$
$=\cfrac{1}{144}(1+1+1-1-1+1)$
$=\cfrac{1}{72}$

したがって

$|\overrightarrow{\text{MP}}|=\sqrt{\cfrac{1}{72}}=\cfrac{\sqrt{2}}{12}$　（答え）