【数学Ⅱ三角関数】これでラジアンが求められる　弧度法が分かるようになる練習問題

古代メソポタミア人が発明した360°

日本人は小学4年生のときに一周360°という概念を習うことになっています。そのあと、私たちは高校2年生までその概念の枠組みの中で思考するように教育されるので、高校2年生で唐突に弧度法なる概念を教え込まれ、混乱する生徒が続出するのです。

360°という概念を発明したのは古代メソポタミア人だと言われています。およそ5000年ほど前の話です。彼らは夜の星空を観測して、星がおよそ360日で北極星の周りを1回転することを知っていました。それをギリシャ人のタレスという人物が角度を表す基準として用いたのが360°の起源だと考えられています。

弧度法の発明

こうして、円の一周は360°ということになります。しかし、よくよく考えてみると360という数値は中途半端だと思いませんか？ 円を100分割するとかの方がまだ納得いく感じがします。

こうして、18世紀ごろに新しい考え方が生まれます。それは、弧の長さをそのまま角度にすればいいじゃん！というものでした。

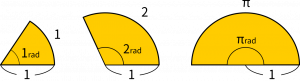
半径1の円において弧の長さが1のとき、その角度1ラジアンとする。弧の長さが2なら2ラジアン、弧の長さがπならπラジアンとしよう！となったのです。これを弧度法と言います。

結局、角度は弧の長さに比例するから、弧の長さをそのまま角度にした方が合理的である、という考えに至るわけです。

弧度法を用いることには利点があります。

みなさんが中学生のときに、円の半径が1で中心角が45°の弧の長さを求めようとするなら、次の計算をしたはずです。

$\displaystyle 2\pi\times1\times\frac{45}{360}=\frac{1}{4}\pi$

この計算は分数の約分が面倒です。しかし、弧度法を覚えたら 45°$\displaystyle =\frac{\pi}{4}$ だから弧の長さは $\displaystyle \frac{\pi}{4}$ だ！ と一発で答えを求めることができます。

弧度法の練習

まずは、180°=π の関係を覚えましょう。そこから考えていきます。

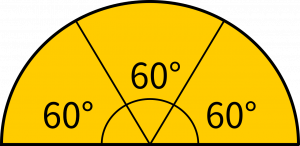
180°を3分割すれば60°になります。180°=π だから、60°は$\displaystyle\frac{\pi}{3}$ です。

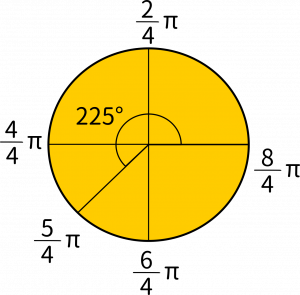
こういう場合は、分母を4にして考えましょう。180°を$\displaystyle\frac{4}{4}\pi$ として考えれば、$\displaystyle\frac{5}{4}\pi$ は180°+45°＝225°になると分かります。

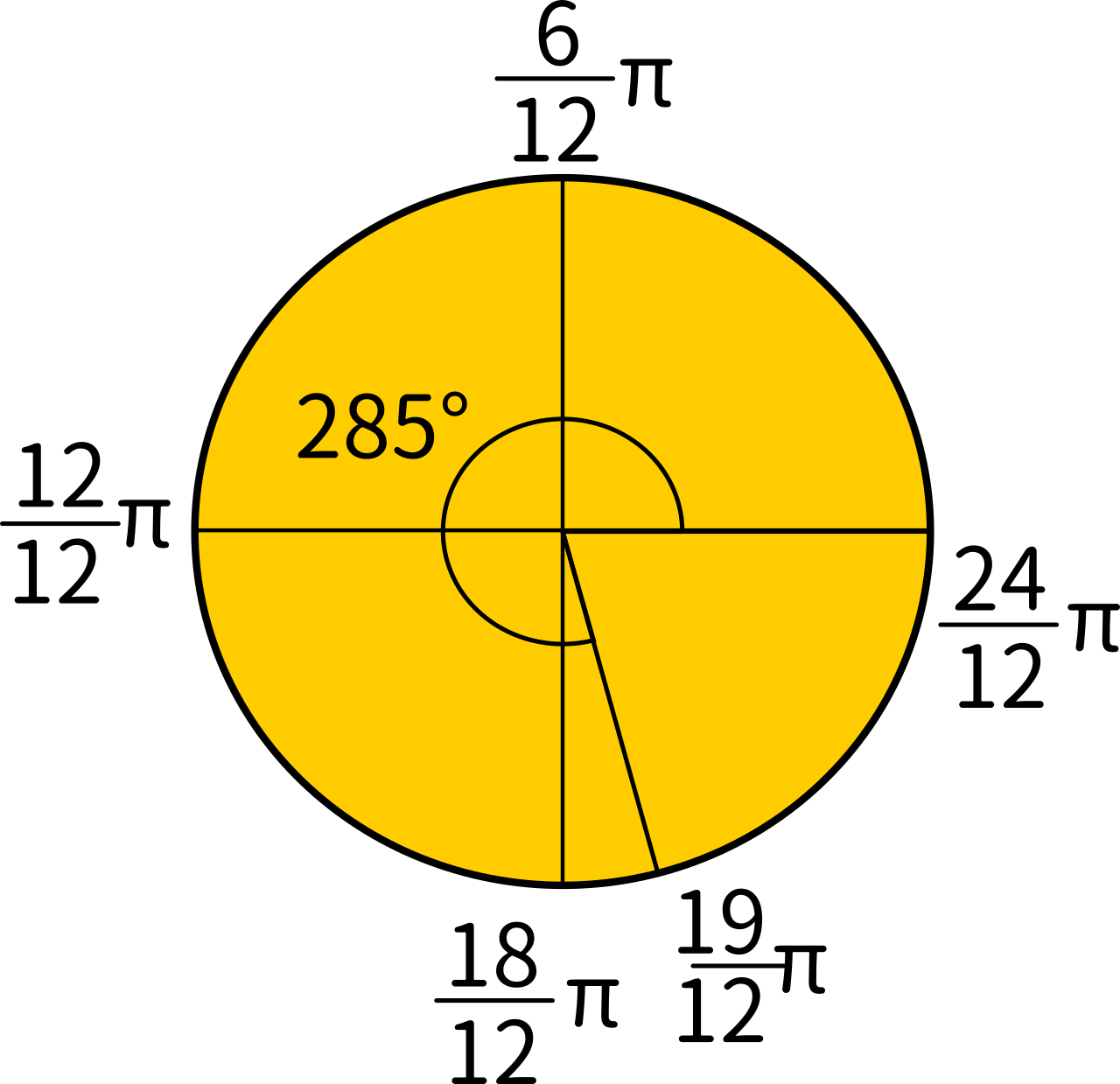
今度は、180°を$\displaystyle\frac{12}{12}\pi$ と考えます。そこから、180°を12分割すれば1つは15°になるので、$\displaystyle\frac{1}{12}\pi$＝15°です。単位円を描いてみると、$\displaystyle\frac{18}{12}\pi$ の位置が270°になるので、それに$\displaystyle\frac{1}{12}\pi$ を加えると $\displaystyle\frac{19}{12}\pi$ になります。つまり270°＋15°＝285°ということです。

弧度法の練習２

今度は角度をラジアンに直してみましょう。

180°を6つに分割すれば30°です。180°=$\pi$ から考えて、$\pi$ を6つに分割した $\displaystyle\frac{\pi}{6}$ が答えです。

慣れるまでは図を描くようにしましょう。

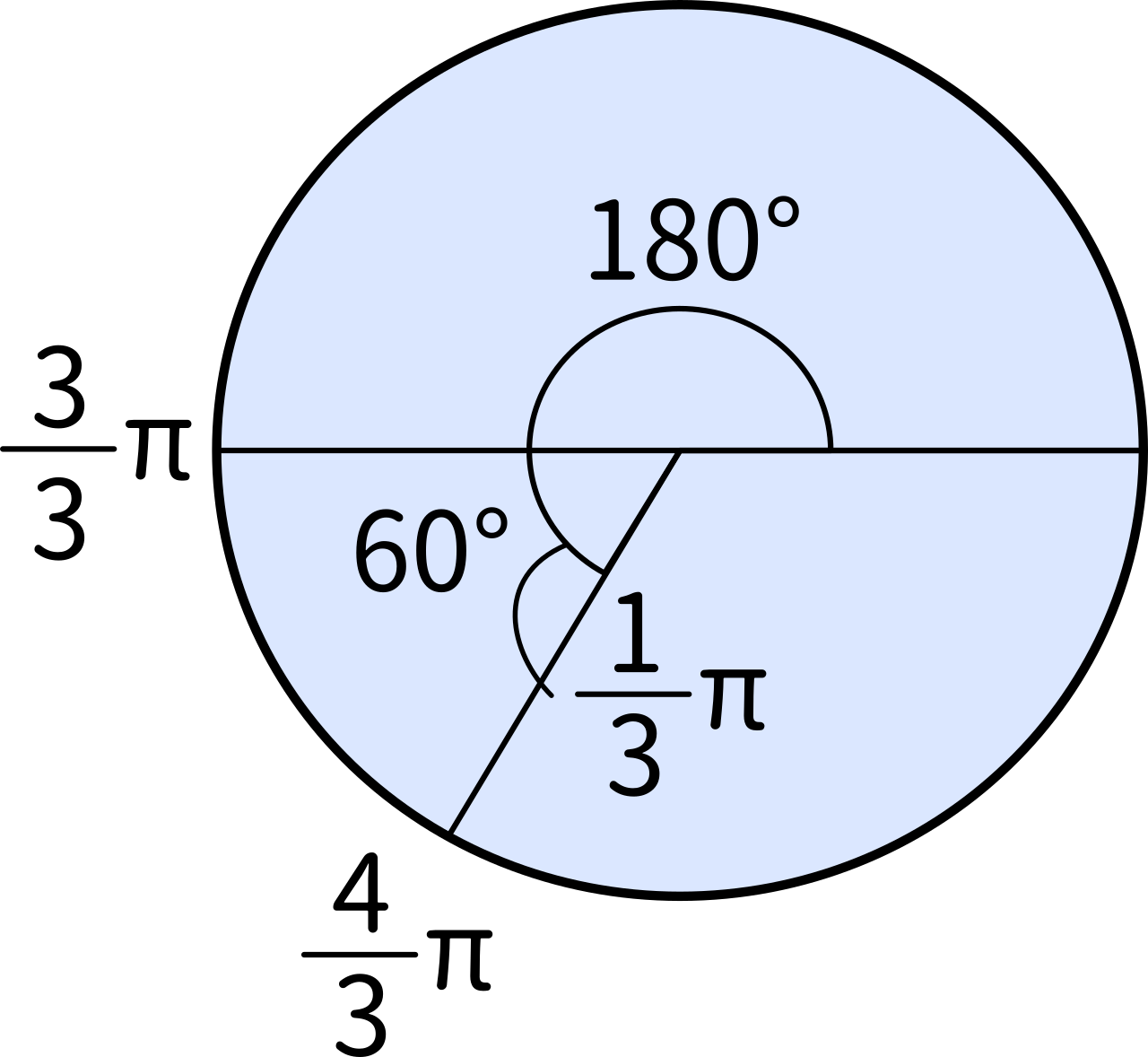
240°は180°＋60°と分割して考えます。60°が$\displaystyle\frac{\pi}{3}$ というのが思い出せれば、$\displaystyle\pi+\frac{1}{3}\pi=\frac{4}{3}\pi$ となります。

360°に近いほうの数が出てきたら、逆向きに考えるのも一つの手です。345°は360°－15°と考えることができます。15°は180°を12分割したもの、つまり$\displaystyle\frac{1}{12}\pi$ です。そこで 12 を分母として考えると、360°は $\displaystyle\frac{24}{12}\pi$ となるので、そこから $\displaystyle\frac{1}{12}\pi$ を引いて、$\displaystyle\frac{23}{12}\pi$ が答えとなります。