【数IIB帰納法・微分】帰納法を用いて数列がすべて整数であることを示す(北海道大2016理系第4問)

(1) 次の方程式が異なる 3 つの 0 でない実数解をもつことを示せ。

$x^3+x^2-2x-1=0$ ・・・・・・①

(2) 方程式①の 3 つの実数解を $s,t,u$ とし，数列 $\{a_n\}$ を

$a_n=\cfrac{s^{n-1}}{(s-t)(s-u)}+\cfrac{t^{n-1}}{(t-u)(t-s)}+\cfrac{u^{n-1}}{(u-s)(u-t)}$
$(n=1,2,3,\cdots)$

によって定める。このとき，

$a_{n+3}+a_{n+2}-2a_{n+1}-a_n=0$ $(n=1,2,3,\cdots)$

が成り立つことを示せ。

(3) (2)の $a_n$ がすべて整数であることを示せ。

(北海道大2016)

増減表から頂点の位置を考える

(1)から始めます。

$f(x)=x^3+x^2-2x-1$ としてグラフを考えるとこのようになります。

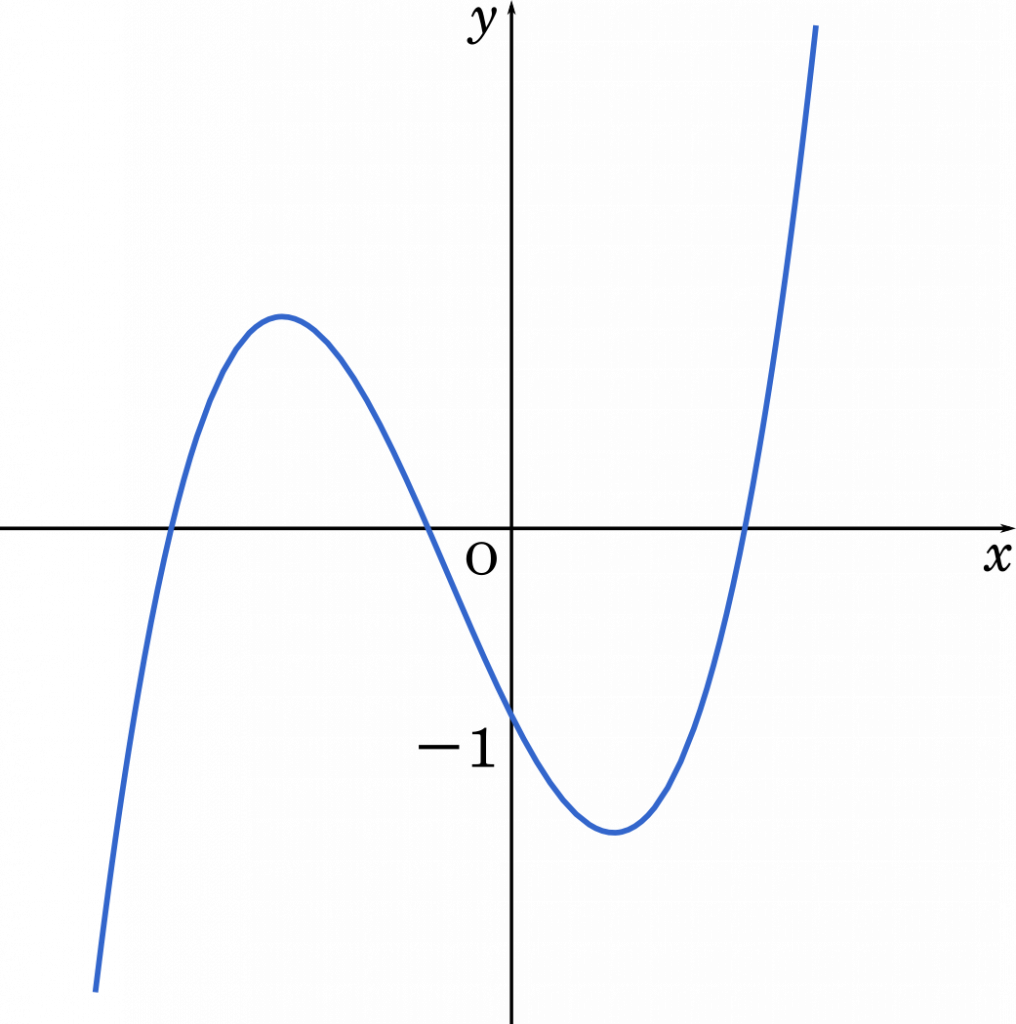
関数の実数解に 0 が含まれないことは $f(0)=-1$ から明らかです（反対に言えば，実数解に 0 が含まれるなら，$f(0)=0$ が成り立ちます）。

そして，グラフを見れば，関数が異なる 3 つの実数解を持つとき，2 つの頂点の $y$ 座標はそれぞれ正と負または負と正の組み合わせになることが分かります。

話を進める上で増減表があった方が良いので，いったん増減表を作りましょう。

$f'(x)=3x^2+2x-2$

$3x^2+2x-2=0$ として

$x=\cfrac{-1\pm\sqrt{7}}{3}$

増減表は

$\def\arraystretch{1.5}\begin{array}{|c||c|c|c|c|c|}\hline x&\cdots&\frac{-1-\sqrt{7}}{3}&\cdots&\frac{-1+\sqrt{7}}{3}&\cdots\\\hline f'(x)&+&0&-&0&+\\\hline f(x)&\nearrow&&\searrow&&\nearrow\\\hline\end{array}$

ここから，$f\Big(\cfrac{-1-\sqrt{7}}{3}\Big)$ が正の数であることを示します。

$-3<-\sqrt{7}<-2$ より

$-4<-1-\sqrt{7}<-3$
$-\cfrac{4}{3}<\cfrac{-1-\sqrt{7}}{3}<-1$

増減表より

$f\Big(\cfrac{-1-\sqrt{7}}{3}\Big)>f(-1)$

であることが分かる。$f(-1)$ を求めると

$f(-1)=1$

となるので

$f\Big(\cfrac{-1-\sqrt{7}}{3}\Big)>1>0$

よって，$f\Big(\cfrac{-1-\sqrt{7}}{3}\Big)$ は正の数である。

また

$2<\sqrt{7}<3$ より

$1<-1+\sqrt{7}<2$

$\cfrac{1}{3}<\cfrac{-1+\sqrt{7}}{3}<\cfrac{2}{3}$

増減表より

$f\Big(\cfrac{1}{3}\Big)>f\Big(\cfrac{-1-\sqrt{7}}{3}\Big)$

であることが分かる。$f\Big(\cfrac{1}{3}\Big)$ を求めると

$f\Big(\cfrac{1}{3}\Big)=\cfrac{1}{27}+\cfrac{1}{9}-\cfrac{2}{3}-1$
$=-\cfrac{5}{9}$

となるので

$0>-\cfrac{5}{9}>f\Big(\cfrac{-1-\sqrt{7}}{3}\Big)$

よって，$f\Big(\cfrac{-1-\sqrt{7}}{3}\Big)$ は負の数である。

したがって，$x^3+x^2-2x-1=0$ は異なる 3 つの実数解を持つ。(証明終わり)

(1)の式を利用することを考えて式変形する

(2)に進みます。

$a_n=\cfrac{s^{n-1}}{(s-t)(s-u)}+\cfrac{t^{n-1}}{(t-u)(t-s)}+\cfrac{u^{n-1}}{(u-s)(u-t)}$

このまま式変形しても良いのですが，計算がかなり大変そうです。

$s,t,u$ は定数だから，分数の分母の部分はすべて定数になります。そこで，いったん別の文字に置き換えて計算していきます。

$a_n=\cfrac{s^{n-1}}{p}+\cfrac{t^{n-1}}{q}+\cfrac{u^{n-1}}{r}$ として

$=\cfrac{1}{pqr}(s^{n-1}qr+t^{n-1}pr+u^{n-1}pq)$

これを $a_{n+3}+a_{n+2}-2a_{n+1}-a_n$ にあてはめていくと

$a_{n+3}=\cfrac{1}{pqr}(s^{n+2}qr+t^{n+2}pr+u^{n+2}pq)$
$a_{n+2}=\cfrac{1}{pqr}(s^{n+1}qr+t^{n+1}pr+u^{n+1}pq)$
$2a_{n+1}=\cfrac{2}{pqr}(s^{n}qr+t^{n}pr+u^{n}pq)$

よって

$a_{n+3}+a_{n+2}-2a_{n+1}-a_n$
$=\cfrac{1}{pqr}\{(s^{n+2}+s^{n+1}-2s^n-s^{n-1})qr+(t^{n+2}+t^{n+1}-2t^n-t^{n-1})pr+(u^{n+2}+u^{n+1}-2u^n-u^{n-1})pq\}$
$=\cfrac{1}{pqr}\{s^{n-1}(s^3+s^2-2s-1)qr+t^{n-1}(t^3+t^2-2t-1)pr+u^{n-1}(u^3+u^2-2u-1)pq\}$

ここで，(1)で登場した方程式①を利用します。

$x^3+x^2-2x-1=0$

つまり

$s^3+s^2-2s-1=0$
$t^3+t^2-2t-1=0$
$u^3+u^2-2u-1=0$

となるので，式は

$=0$

である。（証明終わり）

帰納法を用いて数列の値がすべて整数であることを示す

(3)に進みます。

問題文から言えば，帰納法を用いるところです。

(2)で証明した

$a_{n+3}+a_{n+2}-2a_{n+1}-a_n=0$

は，変形すると

$a_{n+3}=-a_{n+2}+2a_{n+1}+a_n$

という漸化式になります。

帰納法では、まず $n=1$ からスタートでした。

$a_4=-a_3+2a_2+a_1$

もし，$a_1,a_2,a_3$ が整数なら $a_4$ も整数であることは式の形から明らかです。

$n$ を増やしていきます。

$a_5=-a_4+2a_3+a_2$

$a_2,a_3,a_4$ は整数であることが分かっているので，$a_5$ も整数です。

あとは同じことの繰り返しで，$a_n$ はすべて整数であると言えます。

教科書の練習問題では $n=k+1$ の式を作って，それを変形していく作業を行ったと思いますが，今回は式を見れば $a_{n+1}$ が整数であることは明らかなので，そうした作業は必要ありません。

問題は，$a_1,a_2,a_3$ が整数であることを示す作業です。$a_n$ の式の $s,t,u$ はすべて実数であり整数ではありません。したがって，式変形で消去することで，それぞれ整数であることを示します。

$a_n=\cfrac{s^{n-1}}{(s-t)(s-u)}+\cfrac{t^{n-1}}{(t-u)(t-s)}+\cfrac{u^{n-1}}{(u-s)(u-t)}$

式をよくみると，共通因数が作れそうです。

$(t-s)=-(s-t)$
$(u-s)=-(s-u)$
$(u-t)=-(t-u)$

だから

$a_n=\cfrac{s^{n-1}}{(s-t)(s-u)}-\cfrac{t^{n-1}}{(t-u)(s-t)}+\cfrac{u^{n-1}}{(s-u)(t-u)}$
$a_n=\cfrac{(t-u)s^{n-1}-(s-u)t^{n-1}+(s-t)u^{n-1}}{(s-t)(s-u)(t-u)}$

これより

$a_1=\cfrac{t-u-s+u+s-t}{(s-t)(s-u)(t-u)}$
$=0$

整数であることが示されました。同様に

$a_2=\cfrac{(t-u)s-(s-u)t+(s-t)u}{(s-t)(s-u)(t-u)}$
$=\cfrac{st-su-st+tu+su-tu}{(s-t)(s-u)(t-u)}$
$=0$

$a_3=\cfrac{(t-u)s^2-(s-u)t^2+(s-t)u^2}{(s-t)(s-u)(t-u)}$

ここで，分子だけを考えて因数分解していきます。方針としては文字を一つ決めて，降べきの順に並べ替えていくと良いでしょう。どの文字でも構わないのですが，とりあえず $s$ を降べきの順に並べ替えてみます。

$(t-u)s^2-(s-u)t^2+(s-t)u^2$
$=(t-u)s^2-t^2s+t^2u+u^2s-tu^2$
$=(t-u)s^2-(t^2-u^2)s+tu(t-u)$
$=(t-u)s^2-(t+u)(t-u)s+tu(t-u)$
$=(t-u)\{s^2-(t+u)s+tu\}$
$=(t-u)(s-t)(s-u)$

よって

$a_3=1$

これで，$a_1,a_2,a_3$ が整数であることが示されました。あとは，帰納法の手順で証明していきましょう。

$a_{n+3}=-a_{n+2}+2a_{n+1}+a_n$ ・・・(A)

として

[I] $n=1$ のとき

$a_4=-a_3+2a_2+a_1$

$a_1,a_2,a_3$ は整数より，$a_4$ は整数である。

[II] $n=k$ のとき(A)の$a_n,a_{n+1},a_{n+2},a_{n+3}$が整数であると仮定すると，$n=k+1$ のとき
$a_{n+4}=-a_{n+3}+2a_{n+2}+a_{n+1}$

$a_{n+1},a_{n+2},a_{n+3}$ は整数より，$a_{n+4}$ は整数である。

[I]，[II]より，すべての自然数 $n$ において $a_n$ は整数である。(証明終わり)