【数IIB確率分布と統計的な推測②】二項分布を標準正規分布にするときの考え方
前回,読書アンケートで二項分布をざっくり理解してみる で二項分布と正規分布の関係について解説しました。今回は標準正規分布について考えていきます。
標準正規分布
前回,二項分布は近似的に正規分布に従うという話をしました。これをもとに実際に計算を行ってみましょう。
まず,二項分布を正規分布に変換してみます。
二項分布 $B(n,p)$ に従う確率変数 $X$ は,$n$ が十分に大きいとき,近似的に正規分布 $N(np,\sigma^2)$ に従う。

$\sigma$ (シグマと読む)は標準偏差のことです。
ある学校で 100 人の生徒を無作為に選び,読書時間のアンケートを行ったとします。このとき全く読書をしなかった生徒の母比率を 0.5 とし,標準偏差を 5 とします。
このとき,確率変数 $X$ は二項分布 $B(100,0.5)$ に従い,近似的に正規分布 $N(100\times0.5,5^2)$ に従います。つまり $N(50,25)$ です。
このようにして,二項分布をいったん正規分布に置きかえます。


標準正規分布と正規分布表
ここでコンピュータを使えば,正規分布のまま確率を計算することもできます。その他にも,教科書に載っている正規分布表を使って計算を行う方法があります。


正規分布表を記事の最後に掲載しておきます。分布表に載っている数字は確率を表しますが,これは標準正規分布というグラフおける確率です。
正規分布表を利用するためには,正規分布を標準正規分布に変換しなければなりません。


確率変数 $X$ が正規分布 $N(m,\sigma^2)$ に従うとき
$Z=\cfrac{X-m}{\sigma}$
とおくと,確率変数 $Z$ は標準正規分布 $N(0,1)$ に従う。


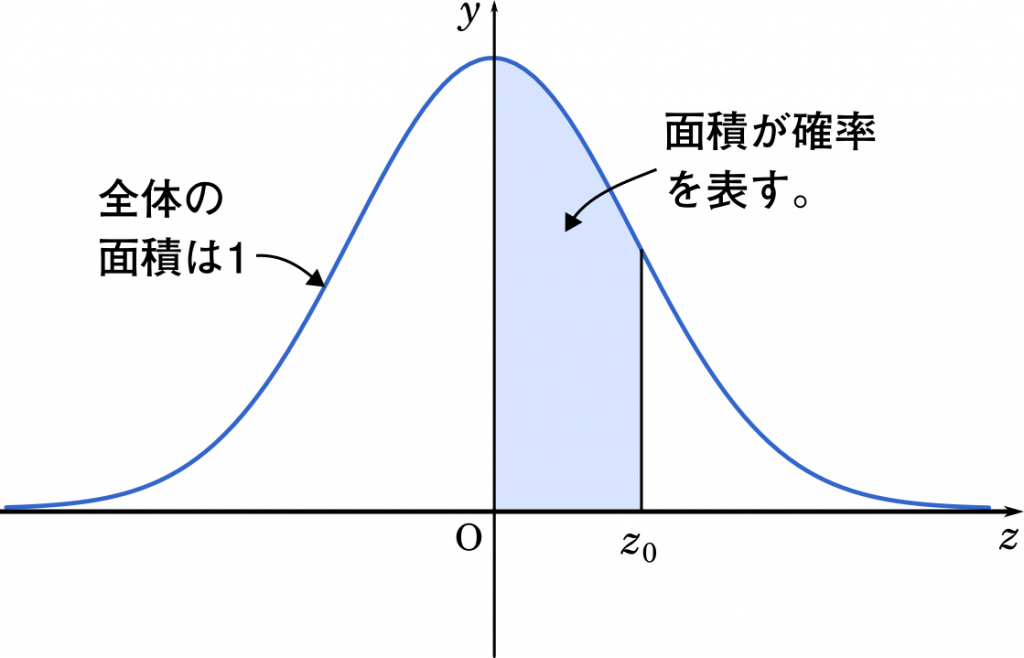
このときグラフを塗りつぶした部分の面積が確率を表します。ちなみにグラフ全体の面積は 1,つまり 100 パーセントを表します。
読書時間の話に戻りましょう。
$N(50,5^5)$ のとき
$Z=\cfrac{X-50}{5}$
とすると,$Z$ は標準正規分布に従います。
ここで,全く読書をしなかった生徒の数が 50 人以上 60 人以下である確率を求めてみましょう。
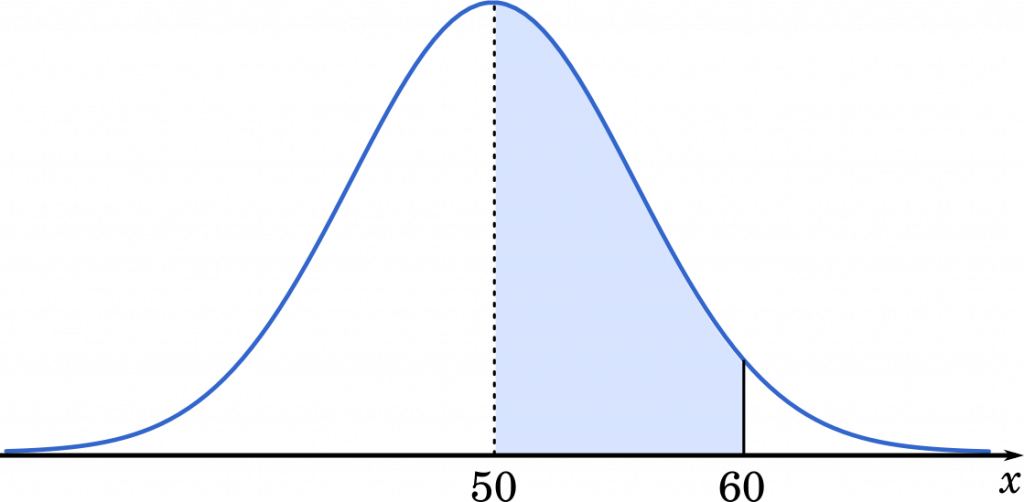
求める確率はグラフの色を塗った部分の面積です。これを,標準正規分布のグラフになおします。
$X=60$ として
$Z=\cfrac{60-50}{5}=2$
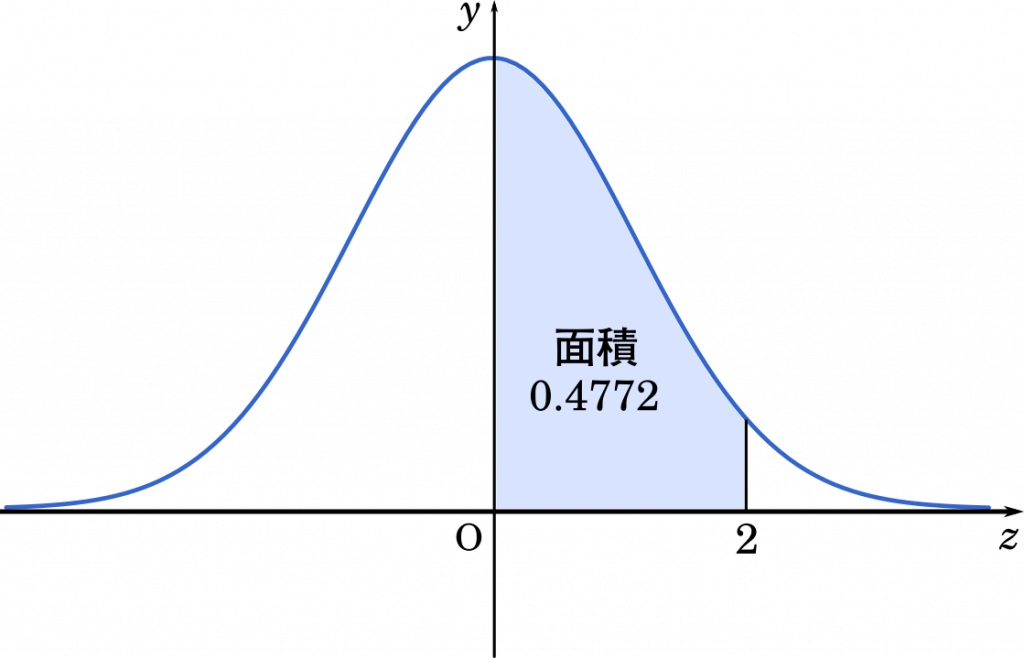
正規分布表の 2.0 の値は 0.4772 です。
確率を $P$ として式で表すとこうなります。
$P(50\leqq X\leqq 60)=P(0\leqq Z\leqq2)$
$=0.4772$




このように,正規分布表を用いると,$Z$ がある範囲の中に存在する確率,というものが求められます。
ここでもう一つ練習してみましょう。今度は,全く読書をしなかった生徒が 36 人以下となる確率を求めます。
上と同様に,$X=36$ として,$Z$ を求めましょう。
$Z=\cfrac{36-50}{5}=-2.8$
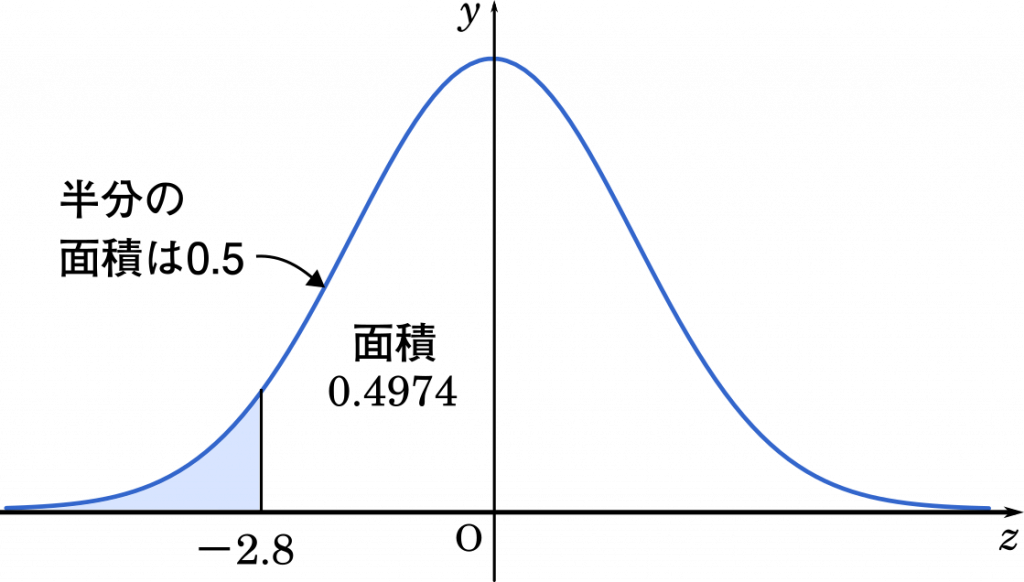
求めたいのはグラフの色を塗った部分の面積です。


グラフは左右対称なので,左側の面積を右側に置き換えても同じことです。
$P(Z<-2.8)=P(2.8<Z)$
グラフ全体の面積は 1 なので,右半分の面積は 0.5 になります。色を塗った部分の面積を求めるには引き算をします。
$P(2.8<Z)=0.5-P(0\leqq Z\leqq2.8)$
$=0.5-0.4974$
$=0.0026$
話をまとめるとこういうことです。ある学校で全く読書をしなかった生徒が全体の 50 パーセントいるとして,そこから 100 人を無作為に抽出します。そのとき,100 人のうち全く読書をしなかった生徒が 36 以下となる確率はおよそ 0.26 パーセントということです。


最後に,正規分布表を掲載します。
正規分布表

SNSでシェア