カージオイド（心臓形）の描き方／曲線の長さを求める(神戸大2016理系第5問)

極方程式で表された $xy$ 平面上の曲線 $r=1+\cos\theta$ $(0\leqq\theta\leqq2\pi)$ を $C$ とする。以下の問に答えよ。

(1) 曲線 $C$ 上の点を直交座標 $(x,y)$ で表したとき，$\cfrac{dx}{d\theta}=0$ となる点，および $\cfrac{dy}{d\theta}=0$ となる点の直交座標を求めよ。

(2) $\displaystyle\lim_{\theta\rightarrow\pi}\cfrac{dy}{dx}$ を求めよ。

(3) 曲線 $C$ の概形を $xy$ 平面上にかけ。

(4) 曲線 $C$ の長さを求めよ。

極値を求める

(1)から始めます。今回描く図形は以下のようになります。

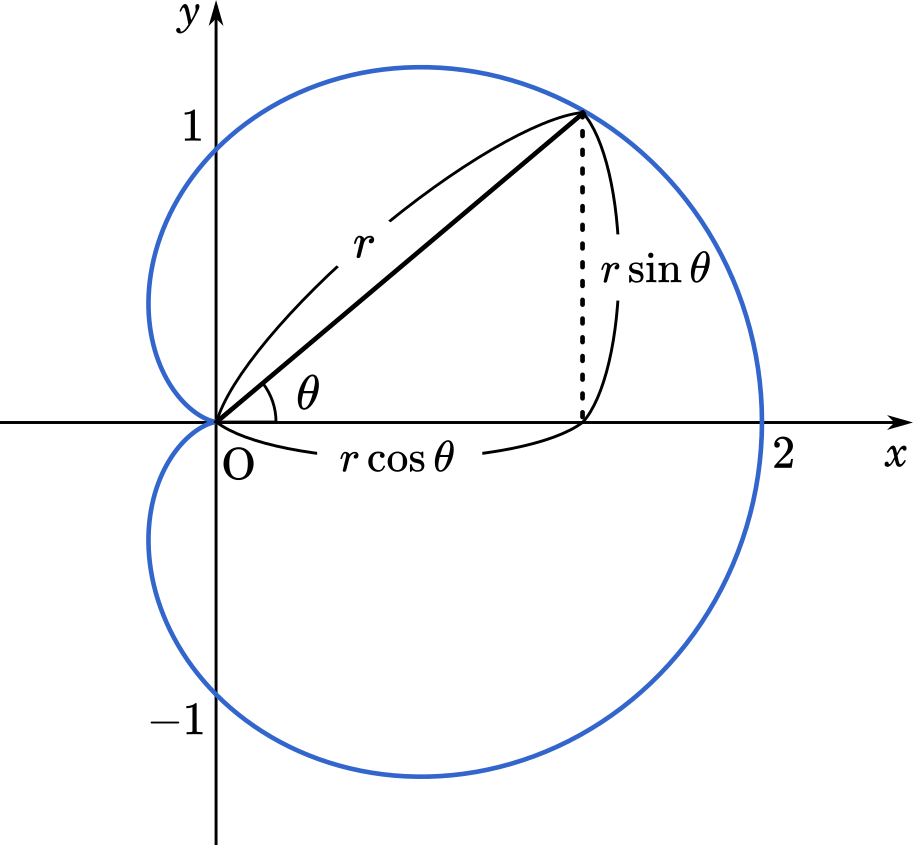
$\theta$ の値によって，$r$ の大きさが変わることによって，上のような図ができあがります。

手順としては，$x$ 座標と $y$ 座標をそれぞれ $\theta$ で微分し，増減表を作って概形を求めます。

$x=r\cos\theta$
$=(1+\cos\theta)\cos\theta$
$=\cos\theta+\cos^2\theta$
$y=r\sin\theta$
$=(1+\cos\theta)\sin\theta$
$=\sin\theta+\sin\theta\cos\theta$

とする。

$x$ を $\theta$ で微分すると

$\cfrac{dx}{d\theta}=-\sin\theta+2\cos\theta(-\sin\theta)$
$=-\sin\theta-2\sin\theta\cos\theta$

$-\sin\theta-2\sin\theta\cos\theta=0$ とすると

$-\sin\theta(1+2\cos\theta)=0$

$\sin\theta=0$ より

$\theta=\pi$

また $\cos\theta=-\cfrac{1}{2}$ だから

$\theta=\cfrac{2}{3}\pi,\cfrac{4}{3}\pi$

$\theta=\pi$ のとき

$r=1+\cos\pi=1-1=0$

よって，$(x,y)=(0,0)$

$\theta=\cfrac{2}{3}\pi$ のとき

$r=1+\cos\cfrac{2}{3}\pi=1-\cfrac{1}{2}=\cfrac{1}{2}$
$x=\cfrac{1}{2}\cos\cfrac{2}{3}\pi=\cfrac{1}{2}\Big(-\cfrac{1}{2}\Big)=-\cfrac{1}{4}$
$y=\cfrac{1}{2}\sin\cfrac{2}{3}\pi=\cfrac{1}{2}\cdot\cfrac{\sqrt{3}}{2}=\cfrac{\sqrt{3}}{4}$
$(x,y)=\Big(-\cfrac{1}{4},\space\cfrac{\sqrt{3}}{4}\Big)$

$\theta=\cfrac{4}{3}\pi$ のとき

$r=1+\cos\cfrac{4}{3}\pi=1-\cfrac{1}{2}=\cfrac{1}{2}$
$x=\cfrac{1}{2}\cos\cfrac{4}{3}\pi=\cfrac{1}{2}\Big(-\cfrac{1}{2}\Big)=-\cfrac{1}{4}$
$y=\cfrac{1}{2}\sin\cfrac{4}{3}\pi=\cfrac{1}{2}\Big(-\cfrac{\sqrt{3}}{2}\Big)=-\cfrac{\sqrt{3}}{4}$
$(x,y)=\Big(-\cfrac{1}{4},-\cfrac{\sqrt{3}}{4}\Big)$

したがって，$\cfrac{dx}{d\theta}=0$ となる点は

$\Big(-\cfrac{1}{4},\pm\cfrac{\sqrt{3}}{4}\Big)$　（答え）

さらに

$y=\sin\theta+\sin\theta\cos\theta$ を $\theta$ で微分すると

$\cfrac{dy}{d\theta}=\cos\theta+\cos\theta\cos\theta-\sin\theta\sin\theta$
$=\cos\theta+\cos^2\theta-\sin^2\theta$
$=\cos\theta+\cos^2\theta-(1-\cos^2\theta)$
$=2\cos^2\theta+\cos\theta-1$

$2\cos^2\theta+\cos\theta-1=0$ とすると

$(2\cos\theta-1)(\cos\theta+1)=0$
$\cos\theta=\cfrac{1}{2},-1$

$\cos\theta=\cfrac{1}{2}$ のとき

$\theta=\cfrac{\pi}{3},\cfrac{5}{3}\pi$

$\theta=\cfrac{\pi}{3}$ のとき

$r=1+\cos\cfrac{\pi}{3}$
$=1+\cfrac{1}{2}=\cfrac{3}{2}$

$x=\cfrac{3}{2}\cos\cfrac{\pi}{3}$
$=\cfrac{3}{2}\cdot\cfrac{1}{2}=\cfrac{3}{4}$

$y=\cfrac{3}{2}\sin\cfrac{\pi}{3}$
$=\cfrac{3}{2}\cdot\cfrac{\sqrt{3}}{2}=\cfrac{3\sqrt{3}}{4}$
$(x,y)=\Big(\cfrac{3}{4},\cfrac{3\sqrt{3}}{4}\Big)$

$\theta=\cfrac{5}{3}\pi$ のとき

$r=1+\cos\cfrac{5}{3}\pi$
$=1+\cfrac{1}{2}=\cfrac{3}{2}$

$x=\cfrac{3}{2}\cos\cfrac{5}{3}\pi$
$=\cfrac{3}{2}\cdot\cfrac{1}{2}=\cfrac{3}{4}$

$y=\cfrac{3}{2}\sin\cfrac{5}{3}\pi$
$=\cfrac{3}{2}\cdot\Big(-\cfrac{\sqrt{3}}{2}\Big)$
$=-\cfrac{3\sqrt{3}}{4}$

$(x,y)=\Big(\cfrac{3}{4},-\cfrac{3\sqrt{3}}{4}\Big)$

また $\cos\theta=-1$ のとき

$\theta=\pi$

$(x,y)=(0,0)$

したがって $\cfrac{dy}{d\theta}=0$ となる点は

$\Big(\cfrac{3}{4},\pm\cfrac{3\sqrt{3}}{4}\Big),(0,0)$　（答え）

極値を求める

(2)に進みます。

$\cfrac{dy}{dx}=\cfrac{\space\cfrac{dy}{d\theta}\space}{\cfrac{dx}{d\theta}}$
$=\cfrac{(2\cos\theta-1)(\cos\theta+1)}{-\sin\theta(2\cos\theta+1)}$

このまま $\theta\rightarrow\pi$ とすると，$\sin\pi=0$ で分母が 0 になってしまうので，極限を求めることができません。

ここは，試行錯誤して 分母の $\sin$ を約分して消去する方法を考えましょう。

$=\cfrac{(2\cos\theta-1)(\cos\theta+1)(\cos\theta-1)}{-\sin\theta(2\cos\theta+1)(\cos\theta-1)}$
$=\cfrac{(2\cos\theta-1)(\cos^2\theta-1)}{-\sin\theta(2\cos\theta+1)(\cos\theta-1)}$
$=\cfrac{(2\cos\theta-1)(1-\sin^2\theta-1)}{-\sin\theta(2\cos\theta+1)(\cos\theta-1)}$
$=\cfrac{-\sin^2\theta(2\cos\theta-1)}{-\sin\theta(2\cos\theta+1)(\cos\theta-1)}$
$=\cfrac{\sin\theta(2\cos\theta-1)}{(2\cos\theta+1)(\cos\theta-1)}$

したがって

$\displaystyle\lim_{\theta\rightarrow\pi}\cfrac{\sin\theta(2\cos\theta-1)}{(2\cos\theta+1)(\cos\theta-1)}$
$=\cfrac{0}{-1\cdot(-2)}=0$　（答え）

グラフの概形を描く

(3)に進みます。いったん(1)で極値を求めているので，あとは増減表を書いてグラフの概形を描きます。

$r=1+\cos\theta$ のグラフは $x$ 軸対称なので，$0$ から $\pi$ までの区間で増減表を作れば大丈夫です。

$\def\arraystretch{1.5}\begin{array}{|c||c|c|c|c|c|c|c|}\hline\theta&0&\cdots&\frac{\pi}{3}&\cdots&\frac{2}{3}\pi&\cdots&\pi\\\hline\frac{dx}{d\theta}&&-&-&-&0&+\\\hline x&2&\searrow&\frac{3}{4}&\searrow&-\frac{1}{4}&\nearrow&0\\\hline\frac{dy}{d\theta}&&+&0&-&-&-\\\hline y&0&\nearrow&\frac{3\sqrt{3}}{4}&\searrow&\frac{\sqrt{3}}{4}&\searrow&0\\\hline\end{array}$

グラフの概形は

曲線の長さ

(4)に進みます。

曲線の長さは次の公式を用います。

$\displaystyle L=2\int_0^{\pi}\sqrt{\Big(\cfrac{dx}{d\theta}\Big)^2+\Big(\cfrac{dy}{d\theta}\Big)^2}\space d\theta$

まずはルートの中を整理していきましょう。

$\Big(\cfrac{dx}{d\theta}\Big)^2+\Big(\cfrac{dy}{d\theta}\Big)^2$
$=\{-\sin\theta(1+2\cos\theta)\}^2+\{(2\cos\theta-1)(\cos\theta+1)\}^2$
$=\sin^2\theta(1+2\cos\theta)^2+(2\cos\theta-1)^2(\cos\theta+1)^2$

ここは式を $\cos$ でまとめた方がいいでしょう。

$=(1-\cos^2\theta)(1+2\cos\theta)^2+(2\cos\theta-1)^2(\cos\theta+1)^2$
$=(1+\cos\theta)(1-\cos\theta)(1+2\cos\theta)^2+(2\cos\theta-1)^2(\cos\theta+1)^2$
$=(1+\cos\theta)\{(1-\cos\theta)(1+2\cos\theta)^2+(2\cos\theta-1)^2(1+\cos\theta)\}$
$=(1+\cos\theta)\{(1-\cos\theta)(1+4\cos\theta+4\cos^2\theta)+(4\cos^2\theta-4\cos\theta+1)(1+\cos\theta)\}$
$=(1+\cos\theta)(1+4\cos\theta+4\cos^2\theta-\cos\theta-4\cos^2\theta-4\cos^3\theta+4\cos^2\theta-4\cos\theta+1+4\cos^3\theta-4\cos^2\theta+\cos\theta)$
$=2(1+\cos\theta)$

$=4\cdot\cfrac{1+\cos\theta}{2}$
$=4\cos^2\cfrac{\theta}{2}$

よって

$\displaystyle L=2\int_0^\pi\sqrt{4\cos^2\cfrac{\theta}{2}}\space d\theta$
$\displaystyle=2\int_0^\pi2\cos\cfrac{\theta}{2}\space d\theta$
$\displaystyle=4\int_0^\pi\cos\cfrac{\theta}{2}\space d\theta$
$=4\Big[2\sin\cfrac{\theta}{2}\Big]_0^\pi$

$=8\Big(\sin\cfrac{\pi}{2}-\sin0\Big)$
$=8$　（答え）