【数III積分】回転体の体積の求め方(九州大)

関数 $\displaystyle f(x)=x-\sin x\space\left(0\leqq x\leqq\frac{\pi}{2}\right)$ を考える。曲線 $y=f(x)$ の接線で傾きが $\displaystyle\frac{1}{2}$ となるものを $\ell$ とする。
(1) $\ell$ の方程式と接点の座標 $(a,b)$ を求めよ。
(2) $a$ は (1) で求めたものとする。曲線 $y=f(x)$、直線 $x=a$、および $x$ 軸で囲まれた領域を、$x$ 軸のまわりに 1 回転してできる回転体の体積 $V$ を求めよ。（九州大2014）

---

傾きから接線を求める

傾きが出てくるので、まずは微分します。
$\displaystyle f'(x)=1-\cos x=\frac{1}{2}$ だから
$\displaystyle x=\frac{\pi}{3}$
$f(x)$ に代入して、$\displaystyle f(x)=\frac{\pi}{3}-\sin\frac{\pi}{3}=\frac{2\pi-3\sqrt{3}}{6}$
よって接点の座標は $\displaystyle (a,b)=\left(\frac{\pi}{3},\frac{2\pi-3\sqrt{3}}{6}\right)$（答え）

ここから接線の式は
$\displaystyle y-\frac{2\pi-3\sqrt{3}}{6}=\frac{1}{2}\left(x-\frac{\pi}{3}\right)$
よって $\displaystyle \ell:\space y=\frac{1}{2}+\frac{\pi-3\sqrt{3}}{6}$（答え）

回転体の体積を求める

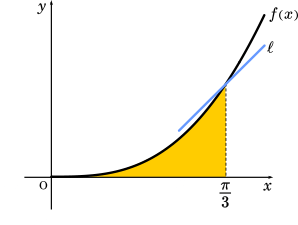
次に回転体の体積を求めます。求める回転体は上の黄色の部分を $x$ 軸を中心にして回転させたものです。体積を求めるイメージは以下のような感じです。

円の面積を重ねていく、つまり積分することで回転体の体積になります。

円の面積を積分する式を作ると
$\displaystyle V=\int_0^{\frac{\pi}{3}} \pi(x-\sin x)^2\space dx$
$\pi$ は定数なので積分の外に出して、2乗を展開します。
$\displaystyle =\pi\int_0^{\frac{\pi}{3}} x^2-2x\sin x+\sin^2 x\space dx$

$\displaystyle =\pi\int_0^{\frac{\pi}{3}} x^2-2x\sin x+\frac{1-\cos {2x}}{2}\space dx$
$\displaystyle =\pi\int_0^{\frac{\pi}{3}} x^2-2x\sin x+\frac{1}{2}-\frac{\cos {2x}}{2}\space dx$

ここで、$\displaystyle \int 2x\sin x\space dx$ を考えてみましょう。

今回は $2x$ を微分したら $2$ になって簡単になりそうなので、$\sin x$ を積分します。

$\displaystyle \int 2x\sin x\space dx$
$\displaystyle =\int 2x(-\cos x)’\space dx$

ここから公式に当てはめて
$\displaystyle =-2x\cos x-\int (2x)'(-\cos x)\space dx$
$\displaystyle =-2x\cos x+2\int \cos x\space dx$
$\displaystyle =-2x\cos x+2\sin x$
これを $V$ の式に当てはめて積分すると
$\displaystyle V=\pi\left[\frac{x^3}{3}-2\sin x+2x\cos x+\frac{x}{2}-\frac{\sin 2x}{4}\right]_0^{\frac{\pi}{3}}$
$\displaystyle =\frac{\pi^4}{81}+\frac{\pi^2}{2}-\frac{9\sqrt{3}}{8}\pi$（答え）