【数III積分】回転体の体積の応用 回転体どうしで引き算(九州大)
原点 O を中心とし、点 A$(0,1)$ を通る円を $S$ とする。点 B$\displaystyle \left(\frac{1}{2},\frac{\sqrt{3}}{2}\right)$ で内接する円 $T$ が、点 C で $y$ 軸に接しているとき、以下の問いに答えよ。
(1) 円 $T$ の中心 D の座標と半径を求めよ。
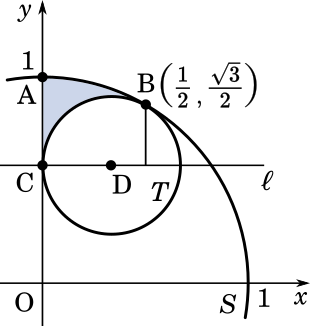
(2) 点 D を通り $x$ 軸に平行な直線を $l$ とする。円 $S$ の短い方の弧 $\overgroup{\text{AB}}$、円 $T$ の短い方の弧 $\overgroup{\text{BC}}$、および線分 AC で囲まれた図形を $l$ のまわりに 1 回転してできる立体の体積を求めよ。(九州大2013)
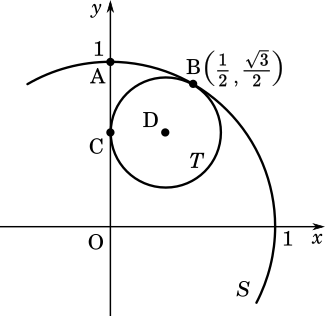

円の中心と半径を求める
回転体に入る前に、(1) を解決しておきます。
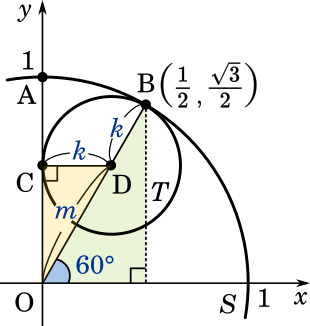
まず、円の中心 D は図で表すとこのような位置にあります。



そして点B の座標から $60\degree$ の直角三角形が 2 つ出来ます。辺の比は $1:2:\sqrt{3}$ だから
$k:m=1:2$
$k+m=1$($k+m$ は円 $S$ の半径になる)
よって $\displaystyle k=\frac{1}{3},m=\frac{2}{3}$
これをもとにして
点D $\displaystyle \left(\frac{1}{3},\frac{\sqrt{3}}{3}\right)$ 半径 $\displaystyle \frac{1}{3}$
回転体の体積を求める
ここから回転体の話です。



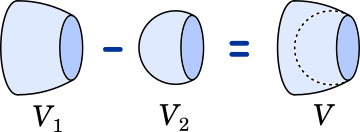


立体を 2 つに分けて考える
まず $V_1$ から。
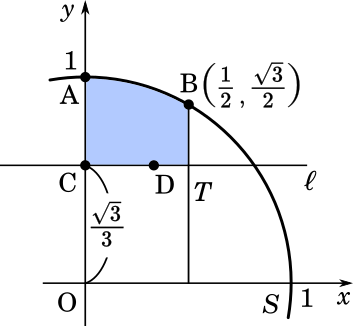
$V_1$ は青い部分の高さを考えます。円 $S$ は原点を中心とする半径 $1$ の円なので
$x^2+y^2=1$
の関係が成り立ちます。これを変形して
$y=\sqrt{1-x^2}$
これは $x$ 軸からの高さを表しているので、引き算して
$\displaystyle y=\sqrt{1-x^2}-\frac{\sqrt{3}}{3}$
となります。これを円の半径として円の面積 $\pi r^2$ を積分すると
$\displaystyle V_1=\pi \int_0^{\frac{1}{2}}\left(\sqrt{1-x^2}-\frac{\sqrt{3}}{3}\right)^2\space dx$
となります。展開して計算していきましょう。
$\displaystyle =\pi\int_0^{\frac{1}{2}} 1-x^2-\frac{2\sqrt{3}}{3}\sqrt{1-x^2}+\frac{1}{3}\space dx$
ルートのついた部分を分けておきます。
$\displaystyle =\pi\int_0^{\frac{1}{2}} \frac{4}{3}-x^2\space dx -\frac{2\sqrt{3}}{3}\pi\int_0^{\frac{1}{2}} \sqrt{1-x^2}\space dx$
ここで
$\displaystyle =\pi\int_0^{\frac{1}{2}} \frac{4}{3}-x^2\space dx$
$\displaystyle =\pi\left[\frac{4}{3}x-\frac{x^3}{3}\right]_0^{\frac{1}{2}}$
$\displaystyle =\pi\left(\frac{2}{3}-\frac{1}{24}\right)=\frac{5}{8}\pi$
置換積分と半角の公式を利用する
また $\displaystyle -\frac{2\sqrt{3}}{3}\pi\int_0^{\frac{1}{2}} \sqrt{1-x^2}\space dx$ を求めると

$x=\sin t$ として
$dx=\cos t\space dt$
$\displaystyle x\space 0\rightarrow \frac{1}{2}$
$\displaystyle t\space 0\rightarrow \frac{\pi}{6}$
よって
$\displaystyle =-\frac{2\sqrt{3}}{3}\pi\int_0^{\frac{\pi}{6}} \sqrt{1-\sin^2 t}\cos t\space dt$
$\displaystyle =-\frac{2\sqrt{3}}{3}\pi\int_0^{\frac{\pi}{6}} \cos^2 t\space dt$
半角の公式 $\displaystyle \cos^2 x=\frac{1+\cos 2x}{2}$ より
$\displaystyle =-\frac{\sqrt{3}}{3}\pi\int_0^{\frac{\pi}{6}} 1+\cos 2t\space dt$
$\displaystyle =-\frac{\sqrt{3}}{3}\pi\left[t+\frac{1}{2}\sin 2t\right]_0^{\frac{\pi}{6}}$
$\displaystyle =-\frac{\sqrt{3}}{3}\pi\left(\frac{\pi}{6}+\frac{\sqrt{3}}{4}\right)$
$\displaystyle =-\frac{\sqrt{3}}{18}\pi^2-\frac{1}{4}\pi$
したがって
$\displaystyle V_1=\frac{5}{8}\pi-\frac{\sqrt{3}}{18}\pi^2-\frac{1}{4}\pi$
$\displaystyle =-\frac{\sqrt{3}}{18}\pi^2+\frac{3}{8}\pi$


もう一つの回転体を考える
次に $V_2$ を求めます。
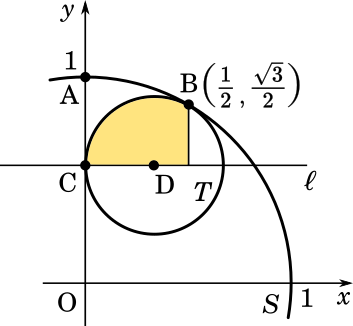
今度は黄色の部分の高さで式を作っていくのですがこのままだと計算が面倒なので中心を原点に移動してしまいましょう。


円の半径は $\displaystyle \frac{1}{3}$ だったので、$x$ 軸方向に $\displaystyle -\frac{1}{3}$ 移動すると、もともとの積分区間 $\displaystyle \left[0,\space\frac{1}{2}\right]$ が $\displaystyle \left[-\frac{1}{3},\space\frac{1}{6}\right]$ になります。
また、円 $T$ は $\displaystyle x^2+y^2=\frac{1}{9}$ の関係が成り立つので、式変形して
$\displaystyle y=\sqrt{\frac{1}{9}-x^2}$
となります。これが回転体の半径です。
よって
$\displaystyle V_2=\pi\int_{-\frac{1}{3}}^{\frac{1}{6}} \left(\sqrt{\frac{1}{9}-x^2}\right)^2\space dx$
$\displaystyle =\pi\int_{-\frac{1}{3}}^{\frac{1}{6}} \frac{1}{9}-x^2\space dx$
$\displaystyle =\pi\left[\frac{1}{9}x-\frac{x^3}{3}\right]_{-\frac{1}{3}}^{\frac{1}{6}}$
$\displaystyle =\frac{1}{24}\pi$
したがって
$\displaystyle V=V_1-V_2=-\frac{\sqrt{3}}{18}\pi^2+\frac{3}{8}\pi-\frac{1}{24}\pi$
$\displaystyle =\frac{1}{3}\pi-\frac{\sqrt{3}}{18}\pi^2$(答え)
SNSでシェア