回転しながら水平方向に移動する動点 Q の描く軌跡(神戸大2017理系第5問)

$r,c,\omega$ は正の定数とする。座標平面上の動点 P は時刻 $t=0$ のとき原点にあり，毎秒 $c$ の速さで $x$ 軸上を正の方向に動いているとする。また，動点 Q は時刻 $t=0$ のとき点 $(0,-r)$ にあるとする。点 P から見て，動点 Q が点 P を中心とする半径 $r$ の円周上を毎秒 $\omega$ ラジアンの割合で反時計回りに回転しているとき，以下の問に答えよ。

(1) 時刻 $t$ における動点 Q の座標 $(x(t),y(t))$ を求めよ。

(2) 動点 Q の描く曲線が交差しない，すなわち，$t_1\not=t_2$ ならば $(x(t_1),y(t_1))\not=(x(t_2),y(t_2))$ であるための必要十分条件を $r,c,\omega$ を用いて与えよ。

Q の座標を求める

(1)から始めます。

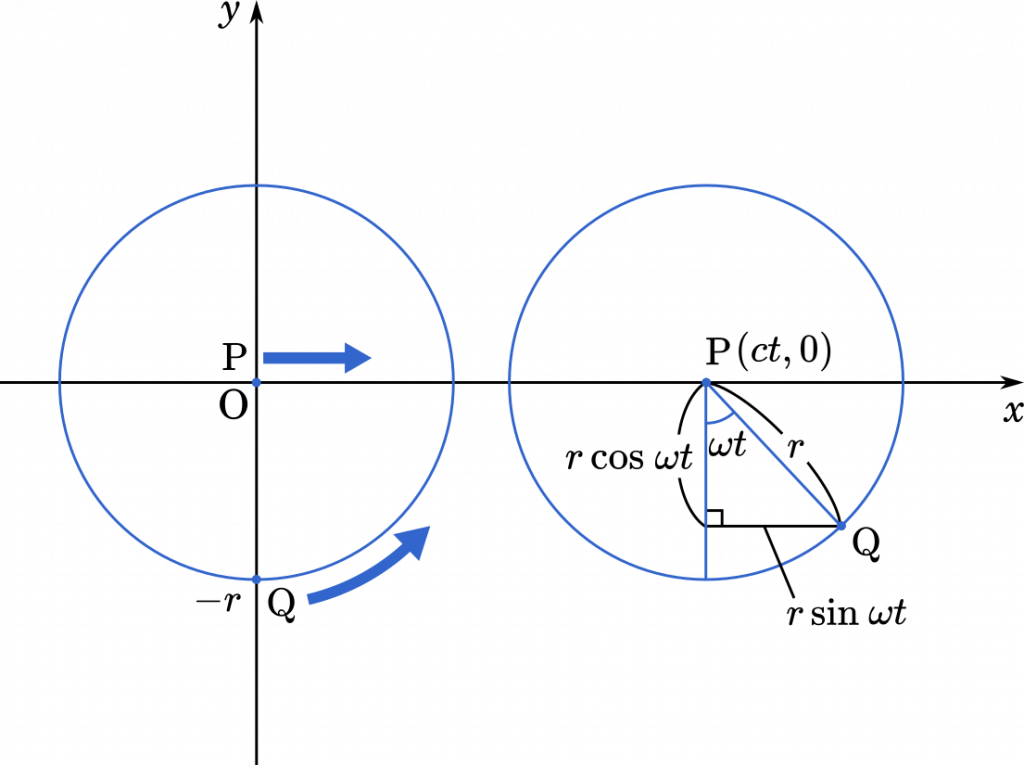
時刻 $t$ における，点 P の座標は

$\text{P}(ct,0)$

となります。また，点 Q の座標は

$x(t)=ct+r\sin\omega t$
$y(t)=-r+(r-r\cos\omega t)$
$=-r\cos\omega t$

よって

$\text{Q}(ct+r\sin\omega t,-r\cos\omega t)$　（答え）

動点 Q の描く軌跡

(2)に進みます。

まずは動点 Q がどのような軌跡を描くかを考えましょう。

$x(t)$，$y(t)$ を微分して，増減表を作ります。

$x(t)=ct+r\sin\omega t$ を $t$ で微分すると

$x'(t)=c+r\omega\cos\omega t$

$\sin\omega t$ は合成関数だから，$\omega t$ を微分した $\omega$ をかけるのを忘れずに。

$c+r\omega\cos\omega t=0$ とすると

$\cos\omega t=-\cfrac{c}{r\omega}$

ここから $t$ の値を求めることはできません。しかし，$0\leqq\omega t\leqq2\pi$ の範囲で，何らかの解が 2 つ存在するだろうということだけは分かります。

ただし，$-\cfrac{c}{r\omega}$ が $-1$ から $1$ の範囲になければ，解は存在しません。

解が存在する場合は極値を持つので，たとえば増加しているグラフが減少する，ということが起きて，$x$ 座標が同じ点が 2 か所以上できる可能性が生まれます。つまり，曲線が交差する可能性があるということです。

逆に，解が存在しない場合は，関数はつねに増加，または減少するので，$y$ 座標が何であろうと曲線は交差しません。

そこで，交差しない条件を考えましょう。

$-\cfrac{c}{r\omega}<-1$ とすると

$\cfrac{c}{r\omega}>1$
$c>r\omega$

このとき

$x'(t)=c+r\omega\cos\omega t$

について考えると，$\cos$ の値は最小で $-1$ です。$c,r,\omega$ が正の数で，かつ $c>r\omega$ なら $x'(t)$ はつねに正の値になります。

また

$-\cfrac{c}{r\omega}=-1$
$\cfrac{c}{r\omega}=1$
$c=r\omega$

この場合，$\cos$ が $-1$ のときに $x'(t)=0$ となりますが，それ以外は $x'(t)$ はつねに正の値です。

今度は $-\cfrac{c}{r\omega}$ が 1 より大きい場合を求めます。

$-\cfrac{c}{r\omega}>1$
$\cfrac{c}{r\omega}<-1$
$c<-r\omega$

$c,r,\omega$ が正の数であることから，この不等式が成り立つ場合はありません。また，$-\cfrac{c}{r\omega}=1$ とすると，$c=-r\omega$ となるので，やはり成り立ちません。

したがって，$c\geqq r\omega$ のとき，動点 Q の描く曲線は交差しない。

今度は，$c<r\omega$ の条件で曲線が交差することを示しましょう。

このとき $x'(t)=0$ は 2 つの実数解をもちます。これらを $\alpha,\beta$ としておきます。

この条件で，今度は $y(t)$ を考えてみましょう。

$y(t)=-r\cos\omega t$
$y'(t)=r\omega\sin\omega t$

$r\omega\sin\omega t=0$ とすると

$\sin\omega t=0$

$0\leqq\omega t\leqq2\pi$ の範囲で

$\omega t=0,\pi,2\pi$
$t=0,\cfrac{\pi}{\omega},\cfrac{2\pi}{\omega}$

ここで，$\omega t=\pi$ のとき，$x'(t)=c-r\omega$ となり，$c<r\omega$ から $x'(t)$ は負の値となります。

また，$\omega t=2\pi$ のとき，$x'(t)=c+r\omega$ となるので，$x'(t)$ は正の値です。

増減表は

$\def\arraystretch{1.5}\begin{array}{|c|c|c|c|c|c|c|c|c|c|}\hline t&0&\cdots&\alpha&\cdots&\frac{\pi}{\omega}&\cdots&\beta&\cdots&\frac{2\pi}{\omega}\\\hline x'(t)&+&+&0&-&-&-&0&+&+\\\hline x(t)&0&\nearrow&&\searrow&&\searrow&&\nearrow\\\hline y'(t)&0&+&+&+&0&-&-&-&0\\\hline y(t)&-r&\nearrow&&\nearrow&r&\searrow&&\searrow&-r\\\hline\end{array}$

よって，$c<r\omega$ のとき曲線は交差する。

したがって，動点 Q の描く曲線が交差しない必要十分条件は

$c\geqq r\omega$　（証明終わり）