【数Ⅰ式と計算】因数分解のいくつか忘れやすいパターンをまとめて復習する

因数分解で忘れがちな３つの作業

$a^3+b^3=(a+b)(a^2-ab+b^2)$ のパターン

問　$x^3+8y^3$　$8y^3$ は $(2y)^3$ で考える

$=(x+2y)(x^2-2xy+4y^2)$ (答え）

$A$ に置き換えパターン

問　$x^6+7x^3-8$　$x^3=A$ として
$A^2+7A-8\\=(A+8)(A-1)\\=(x^3+8)(x^3-1)\\=(x+2)(x^2-2x+4)(x-1)(x^2+x+1)\\=(x-1)(x+2)(x^2+x+1)(x^2-2x+4)$

（答え）

係数をそろえて $A$ に置き換え

問　$(x+1)(x+2)(x+4)(x+5)-10$

順番を並べかえて

$=(x+1)(x+5)(x+2)(x+4)-10\\=(x^2+6x+5)(x^2+6x+8)-10$

$x^2+6x=A$ として

$=(A+5)(A+8)-10\\=A^2+13A+40-10\\=A^2+13A+30$

ここから因数分解

$=(A+3)(A+10)\\=(x^2+6x+3)(x^2+6x+10)$

（答え）

たすきがけ（複雑なやつ）(1)

問　$a^2(b+c)+b^2(c+a)+c^2(a+b)+2abc$

$=a^2b+a^2c+b^2c+ab^2+ac^2+bc^2+2abc$

$a^2$ の項→$a$ の項→それ以外、で並べる

$=(b+c)a^2+(b^2+c^2+2bc)a+b^2c+bc^2\\=(b+c)a^2+(b+c)^2a+bc(b+c)$

$(b+c)$ が共通しているので

$=(b+c)\left\{a^2+(b+c)a+bc\right\}\\=(b+c)(a+b)(a+c)\\=(a+b)(a+c)(b+c)$

（答え）

たすきがけ（複雑なやつ）(2)

問　$2x^2+5xy+2y^2-x+4y-6$

　$x$ を基準に降べきの順で並べかえ

$=2x^2+(5y-1)x+2y^2+4y-6\\=2x^2+(5y-1)x+2(y^2+2y-3)\\=2x^2+(5y-1)x+2(y+3)(y-1)$

　ここから、たすきがけをする

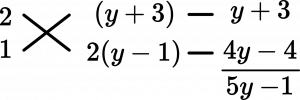
$=(2x+y+3)(x+2y-2)$ （答え）

チャレンジ問題

問　$a^3b-ab^3+b^3c-bc^3+c^3a-ca^3$

$a$ について降べきの順に並べる

$=a^3b-ca^3-ab^3+c^3a+b^3c-bc^3\\=(b-c)a^3-(b^3-c^3)a+bc(b^2-c^2)\\=(b-c)a^3-(b^3-c^3)a+bc(b+c)(b-c)$

　ここで $a^3-b^3=(a-b)(a^2+ab+b^2)$ の公式を思い出す

$=(b-c)a^3-(b-c)(b^2+bc+c^2)a+bc(b+c)(b-c)$

$(b-c)$ が共通しているので

$=(b-c)\left\{a^3-(b^2+bc+c^2)a+bc(b+c)\right\}$

　展開する

$=(b-c)(a^3-ab^2-abc-ac^2+b^2c+bc^2)$

$b$ について降べきの順で並べかえると

$=(b-c)(-ab^2+b^2c-abc+bc^2+a^3-ac^2)\\=(b-c)\left\{(c-a)b^2+(c^2-ac)b+a(a^2-c^2)\right\}\\=(b-c)\left\{(c-a)b^2+c(c-a)b+a(a+c)(a-c)\right\}\\=(b-c)\left\{(c-a)b^2+c(c-a)b-a(c+a)(c-a)\right\}$

$(c-a)$ が共通しているので

$=(b-c)(c-a)\left\{b^2+bc-a(c+a)\right\}\\=(b-c)(c-a)(b-a)(b+c+a)\\=(b-a)(b-c)(c-a)(a+b+c)$

（答え）