【数ⅡBベクトル】位置ベクトルの意味が分からない 三角形の重心


位置ベクトルの考え方










重心を求める方法その1


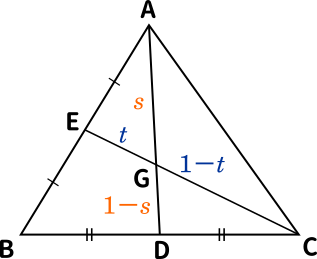
問題 三角形ABCにおいて、AE=BE、BD=CD とするとき、AG:GDを求めよ。


内分点の公式より
$\displaystyle\overrightarrow{\text{AD}}=\frac{1\cdot\overrightarrow{\text{AB}}+1\cdot\overrightarrow{\text{AC}}}{1+1}=\frac{1}{2}\overrightarrow{\text{AB}}+\frac{1}{2}\overrightarrow{\text{AC}}$
また $\overrightarrow{\text{AG}}=k\overrightarrow{\text{AD}}$ とおくと
$\displaystyle\overrightarrow{\text{AG}}=\frac{1}{2}k\overrightarrow{\text{AB}}+\frac{1}{2}k\overrightarrow{\text{AC}}\cdots$①
さらに点Gを辺ECの内分点として式を作ると
$\overrightarrow{\text{AG}}=(1-t)\overrightarrow{\text{AE}}+t\overrightarrow{\text{AC}}$
$\displaystyle\overrightarrow{\text{AE}}=\frac{1}{2}\overrightarrow{\text{AB}}$ だから
$\displaystyle\overrightarrow{\text{AG}}=\frac{1}{2}(1-t)\overrightarrow{\text{AB}}+t\overrightarrow{\text{AC}}\cdots$②
①、②より係数を比べて
$\displaystyle\frac{1}{2}k=\frac{1}{2}(1-t)\cdots$③
$\displaystyle \frac{1}{2}k=t\cdots$④
③、④より
$\displaystyle\frac{1}{2}k=\frac{1}{2}(1-\frac{1}{2}k)$
$\displaystyle k=\frac{2}{3}$
したがって、AG:DG=2:1 (答え)

重心を求める方法2
問題 A$(\vec{a})$、B$(\vec{b})$、C$(\vec{c})$、D$(\vec{d})$、E$(\vec{e})$、G$(\vec{g})$ とするとき、$\vec{g}$ を $\vec{a}$、$\vec{b}$、$\vec{c}$ を用いて表せ。


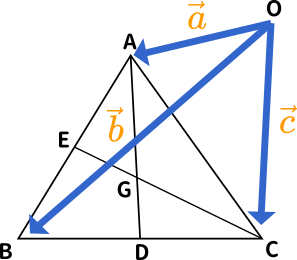

$\overrightarrow{\text{AB}}=\overrightarrow{\text{OB}}-\overrightarrow{\text{OA}}=\vec{b}-\vec{a}$
として表せる。




点D、Eはそれぞれ中点だから
$\displaystyle\vec{e}=\frac{1}{2}\vec{a}+\frac{1}{2}\vec{b}$
$\displaystyle\vec{d}=\frac{1}{2}\vec{b}+\frac{1}{2}\vec{c}$
$\vec{g}=(1-t)\vec{e}+t\vec{c}$
$\displaystyle\vec{g}=\frac{1}{2}(1-t)\vec{a}+\frac{1}{2}(1-t)\vec{b}+t\vec{c}\cdots$①
また
$\vec{g}=(1-s)\vec{a}+s\vec{d}$
$\displaystyle\vec{g}=(1-s)\vec{a}+\frac{1}{2}s\vec{b}+\frac{1}{2}s\vec{c}\cdots$②
①、②より係数を比べて
$\displaystyle\frac{1}{2}(1-t)=1-s\cdots$③
$\displaystyle\frac{1}{2}(1-t)=\frac{1}{2}s\cdots$④
$\displaystyle t=\frac{1}{2}s\cdots$⑤
③、④より
$\displaystyle 1-s=\frac{1}{2}s$
$\displaystyle s=\frac{2}{3}$
②に代入して
$\displaystyle\vec{g}=(1-\frac{2}{3})\vec{a}+\frac{1}{2}\cdot\frac{2}{3}\vec{b}+\frac{1}{2}\cdot\frac{2}{3}\vec{c}$
$\displaystyle\vec{g}=\frac{\vec{a}+\vec{b}+\vec{c}}{3}$ (答え)

SNSでシェア