2 つの二次関数で囲まれた図形の面積の求め方－最小値を微分で求める(東京都立大2018理系第1問)

実戦問題

$a$ を $a>1$ をみたす実数とし，2 つの放物線 $y=x^2$ と $y=a(x^2-1)$ をそれぞれ $C_1$，$C_2$ とする。以下の問いに答えなさい。（東京都立大2018）
(1) $C_1$ と $C_2$ の 2 つの交点の座標を求めなさい。
(2) $C_1$ と $C_2$ で囲まれた部分の面積 $S(a)$ を求めなさい。
(3) (2)で求めた $S(a)$ を最小にする $a$ の値，およびそのときの $S(a)$ の値を求めなさい。

式を連立して交点を求める

(1)から始めます。
$C_1: y=x^2$
$C_2: y=a(x^2-1)=ax^2-a$
グラフは以下のようになります。

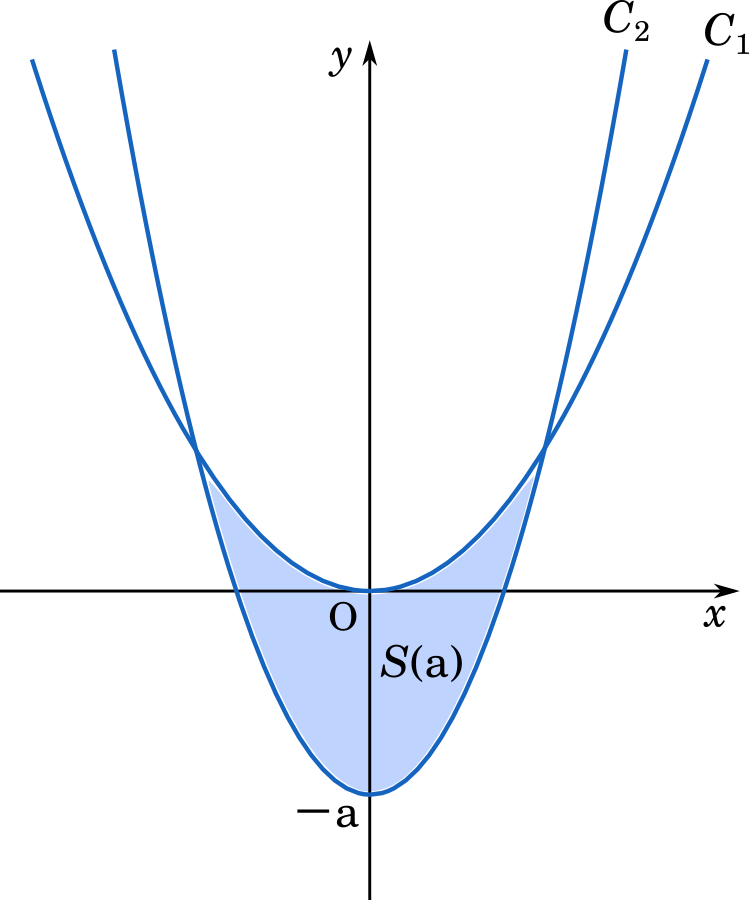
式を連立して交点を求めましょう。
$x^2=ax^2-a$
$ax^2-x^2=a$
$(a-1)x^2=a$
$x^2=\cfrac{a}{a-1}$
$x=\pm\sqrt{\cfrac{a}{a-1}}$
$x$ の値を，それぞれ $y=x^2$ に代入すると，交点の座標は
$\Big(-\sqrt{\cfrac{a}{a-1}},\space\cfrac{a}{a-1}\Big),\space\Big(\sqrt{\cfrac{a}{a-1}},\space\cfrac{a}{a-1}\Big)$
（答え）

積分で面積を求める

(2)に進みます。
今度は積分で面積を求めましょう。グラフは $y$ 軸対称の形なので，面積の半分を求めてそれを 2 倍した方が速く求められます。

$\displaystyle S(a)=2\int_0^{\small{\sqrt{\frac{a}{a-1}}}}x^2-a(x^2-1)\space dx$
$\displaystyle=2\int_0^{\small{\sqrt{\frac{a}{a-1}}}}x^2-ax^2+a\space dx$
$\displaystyle=2\int_0^{\small{\sqrt{\frac{a}{a-1}}}}(1-a)x^2+a\space dx$
$\displaystyle=2\Big[\cfrac{1-a}{3}x^3+ax\Big]_0^{\small{\sqrt{\frac{a}{a-1}}}}$
$=2\Big\{\cfrac{1-a}{3}\Big(\sqrt{\cfrac{a}{a-1}}\Big)^3+a\sqrt{\cfrac{a}{a-1}}\Big\}$
$=2\sqrt{\cfrac{a}{a-1}}\Big(\cfrac{1-a}{3}\cdot\cfrac{a}{a-1}+a\Big)$
$=2\sqrt{\cfrac{a}{a-1}}\Big\{\cfrac{-(a-1)}{3}\cdot\cfrac{a}{a-1}+a\Big\}$
$=2\sqrt{\cfrac{a}{a-1}}\Big\{-\cfrac{a}{3}+a\Big\}$
$=2\sqrt{\cfrac{a}{a-1}}\cdot\cfrac{2}{3}a$
$=\cfrac{4a}{3}\sqrt{\cfrac{a}{a-1}}$
（答え）

微分して面積を最小値を求める

(3)に進みます。
$S(a)=\cfrac{4a}{3}\sqrt{\cfrac{a}{a-1}}$
$=\cfrac{4}{3}\sqrt{\cfrac{a^3}{a-1}}$
として
$\cfrac{a^3}{a-1}$ の最小値を考えます。
$f(a)=\cfrac{a^3}{a-1}$ とする。

$f'(a)=\cfrac{(a^3)'(a-1)-a^3(a-1)’}{(a-1)^2}$
$=\cfrac{3a^2(a-1)-a^3}{(a-1)^2}$
$=\cfrac{3a^3-3a^2-a^3}{(a-1)^2}$
$=\cfrac{2a^3-3a^2}{(a-1)^2}$
$=\cfrac{a^2(2a-3)}{(a-1)^2}$
ここで $\cfrac{a^2(2a-3)}{(a-1)^2}=0$ とすると
問題文より，$a>1$ だから $a^2\not=0$
よって
$2a-3=0$
$a=\cfrac{3}{2}$
増減表は
$\def\arraystretch{1.5}\begin{array}{|c|c|c|c|c|}\hline a&(1)&\cdots&\frac{3}{2}&\cdots\\\hline f'(a)&&-&0&+\\\hline f(a)&&\searrow&&\nearrow\\\hline\end{array}$
最小値は $a=\cfrac{3}{2}$ のとき
$S\Big(\cfrac{3}{2}\Big)=\cfrac{4}{3}\cdot\cfrac{3}{2}\sqrt{\cfrac{\cfrac{3}{2}}{\cfrac{3}{2}-1}}$
$=2\sqrt{\cfrac{\enspace\cfrac{3}{2}\enspace}{\cfrac{1}{2}}}$
$=2\sqrt{3}$
したがって
$S(a)$ の最小値は，$a=\cfrac{3}{2}$ のとき $2\sqrt{3}$　（答え）