【数Ⅲ複素数平面】図形の回転と等比数列の和
複素平面上に点 $P_0(0),P_1(1),P_2,P_3,\cdots$ を図のようにとる。ただし、
$\displaystyle\begin{cases}\angle P_{n-1}P_nP_{n+1}=120\text{°}\\\displaystyle P_nP_{n+1}=\frac{1}{2}P_{n-1}P_n\end{cases}$
$\enspace (n=1,2,\cdots)$
このとき、$P_n$ を表す複素数を求めよ。
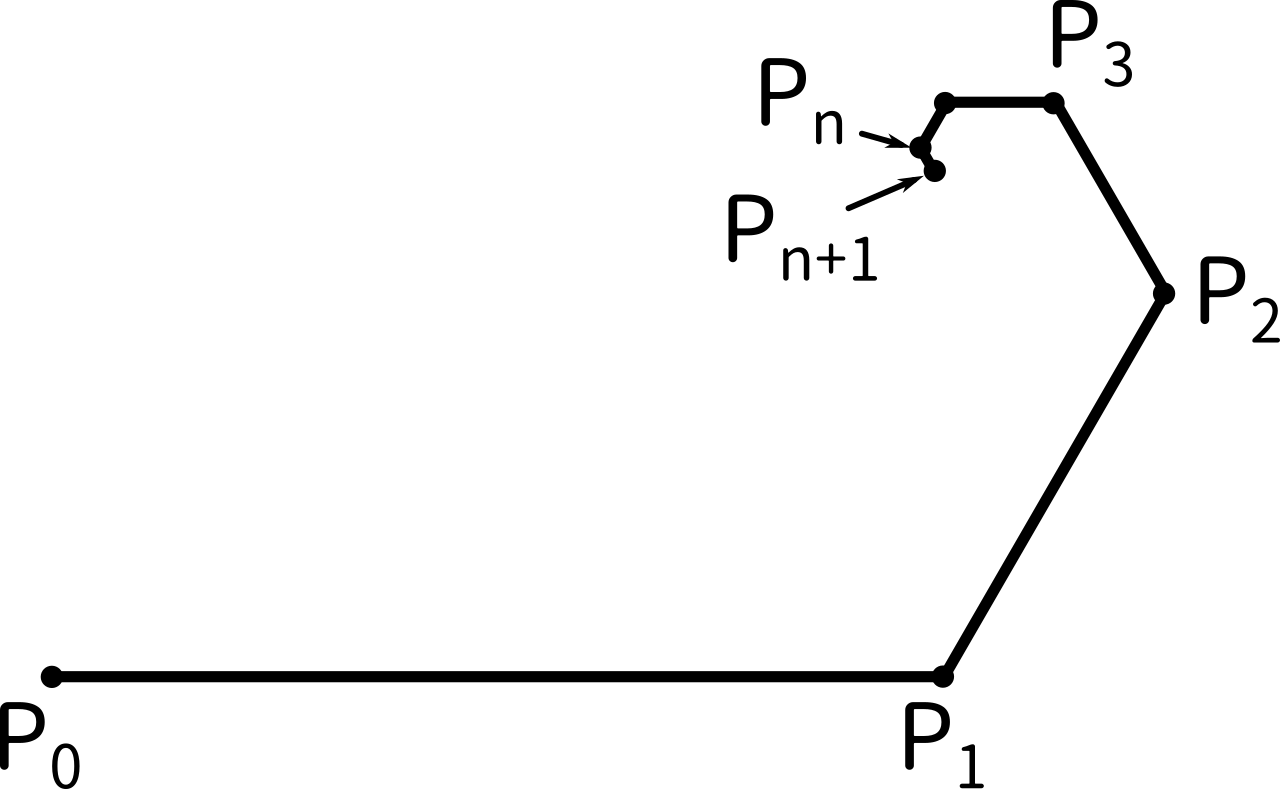


複素数平面における図形の回転
[student]
$\displaystyle\begin{cases}\angle P_{n-1}P_nP_{n+1}=120\text{°}\\\displaystyle P_nP_{n+1}=\frac{1}{2}P_{n-1}P_n\end{cases}$
って何言ってるか分からない。

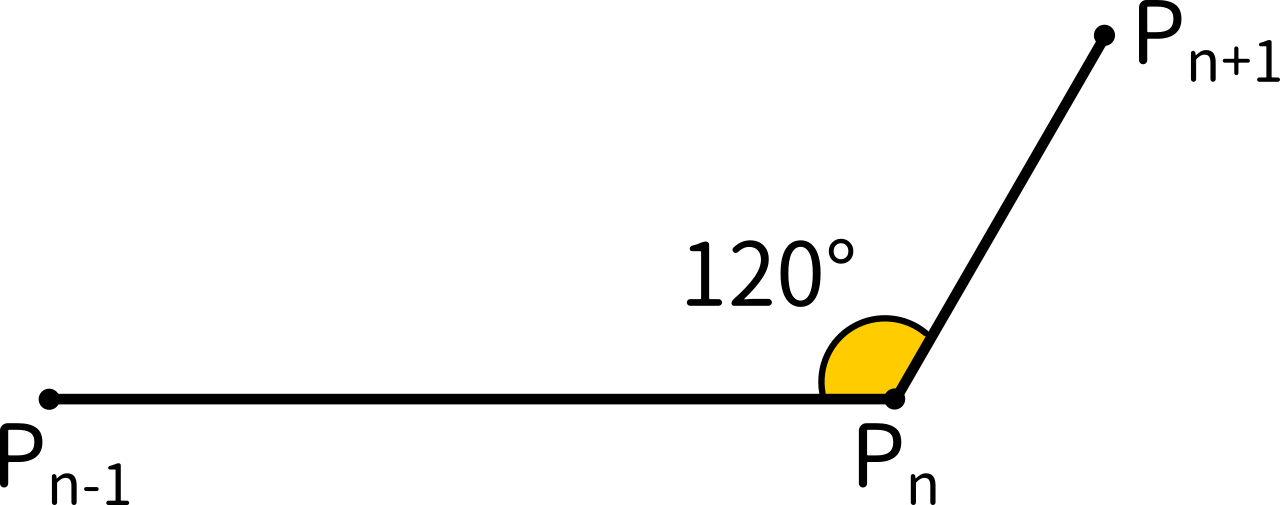






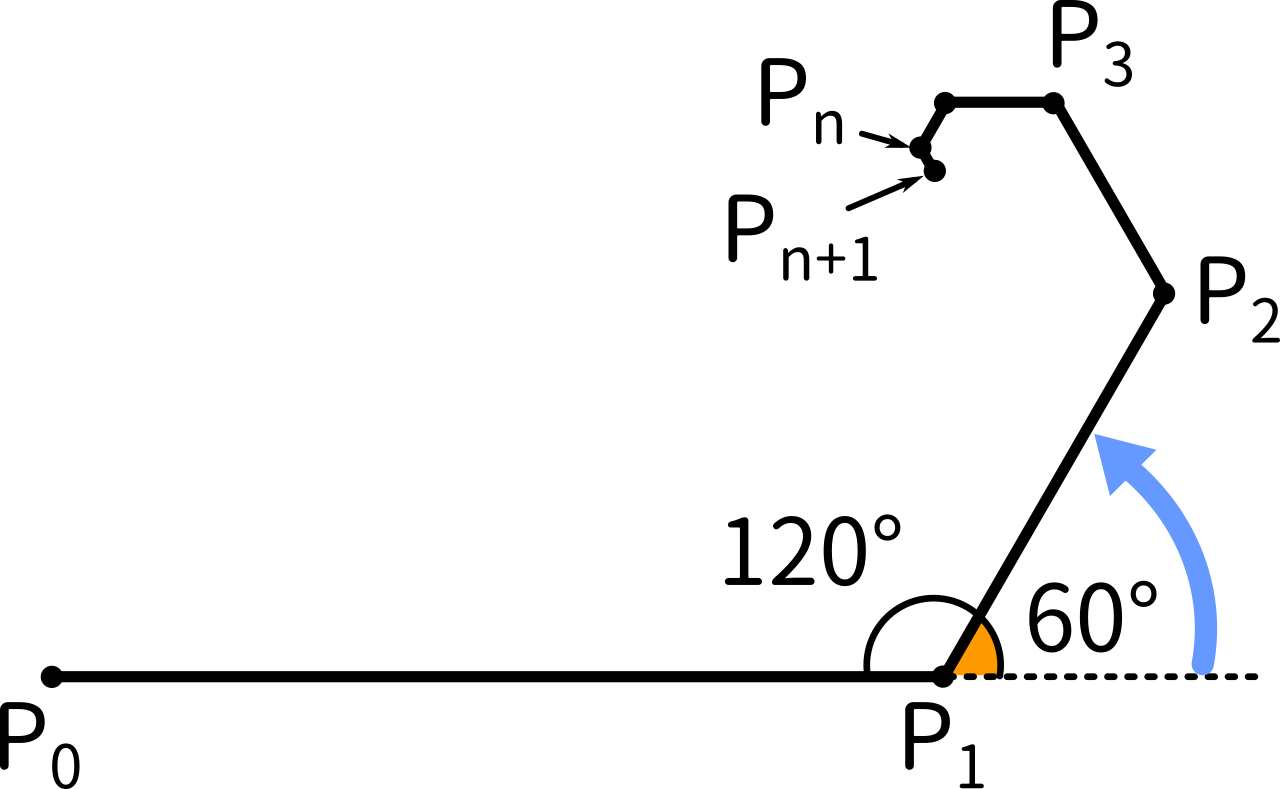
複素数平面における図形の回転は、角度を極座標で表してかけ算をすればよかったことを思い出しましょう。60°回転させて長さを $ \displaystyle\frac{1}{2}$ にするなら、
$\displaystyle\frac{1}{2}(\cos 60\text{°}+i\sin 60\text{°})$
をかけます。
ここで、いったんこの式を計算して $\alpha$ とします。
$\displaystyle\alpha=\frac{1}{2}(\cos 60\text{°}+i\sin 60\text{°})\\\displaystyle=\frac{1}{2}\left(\frac{1}{2}+\frac{\sqrt3}{2}i\right)\\\displaystyle=\frac{1+\sqrt3 i}{4}$
始点が原点 $O$ で始まる場合は単にかけ算すればいいのですが、始点が原点でない場合は、いったん始点を原点に戻す→回転→始点をもとに戻す、という作業が必要になります。
例えば、$P_3$ を求める場合は、このようになります。
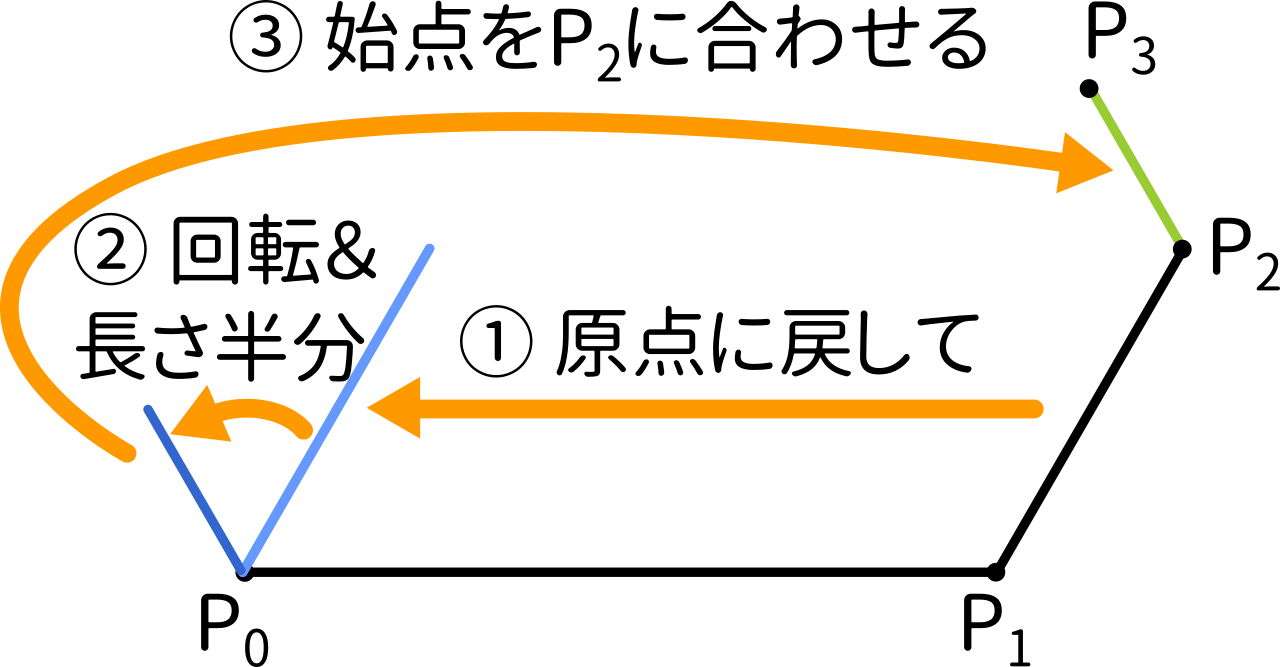
これを式で表すとこうなります。
$P_3=(P_2-P_1)\alpha+P_2$

Pnを求める数列を作る
ここから、この式を $n$ で表してみましょう。$P_2$ を $n$ とすると
$P_{n+1}=(P_n-P_{n-1})\alpha+P_n\\P_{n+1}-P_n=(P_n-P_{n-1})\alpha\enspace\cdots\text{①}$
となります。
$P_n-P_{n-1}$ は、一つの直線を表しています。
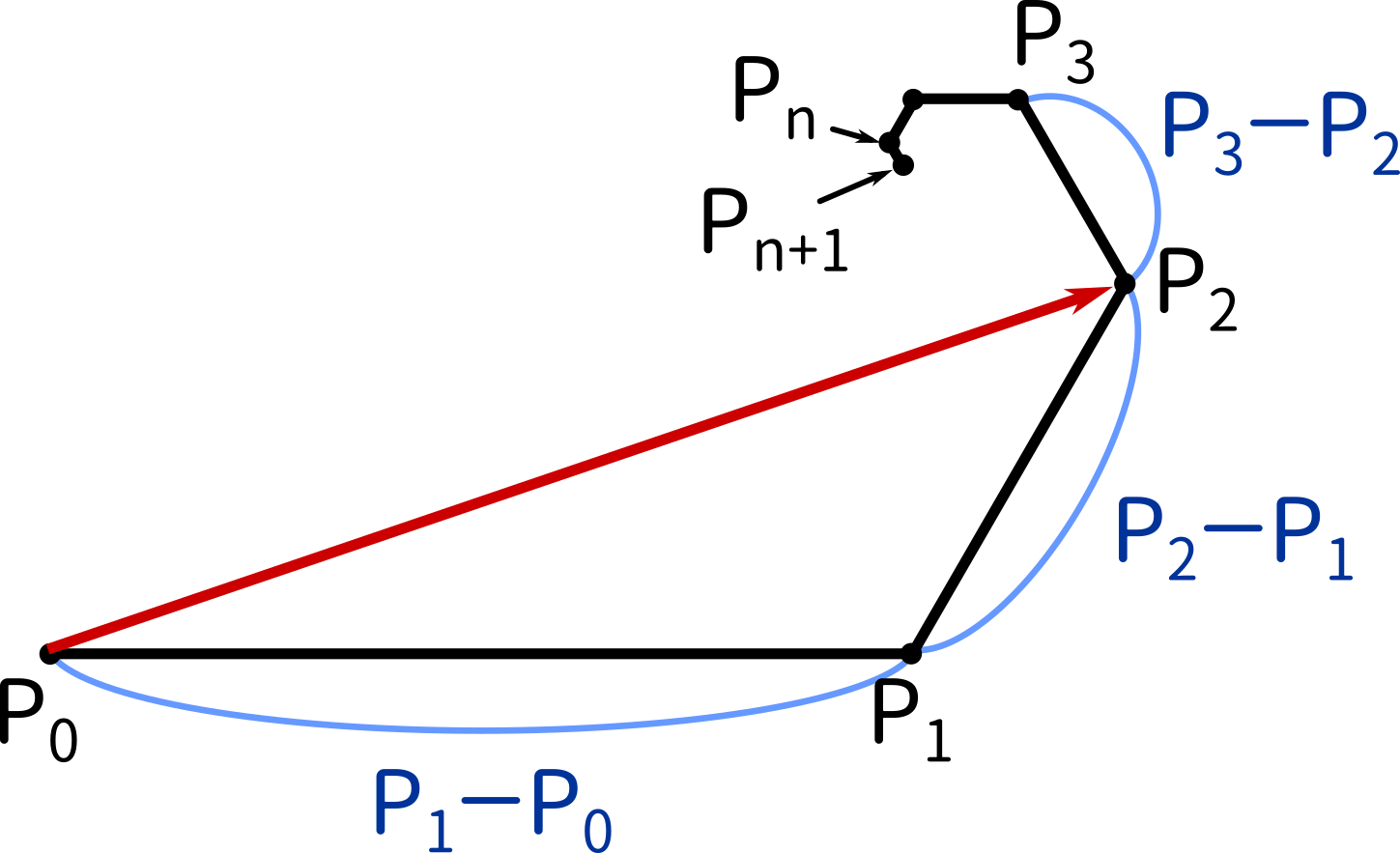

ここで、例えば $P_3$ を考えると、3本の直線を足し合わせればよいことが分かります。
$P_3=(P_1-P_0)+(P_2-P_1)+(P_3-P_2)\enspace\cdots\text{②}$
ここで、①の $P_n-P_{n-1}$ を $b_n$ とすると
$b_{n+1}=b_n\alpha\enspace\cdots\text{①}’$

②にあてはめてみると
$P_3=b_{1}+b_{2}+b_{3}$


等比数列の和の公式を用いてPnを求める
数列 $b_n$ の初項は $n=1$ のときです。よって、初項は $P_1-P_0=1-0=1$ です。また、公比は $\alpha$ でした。
これを公式を使って和を求めると
$\displaystyle\frac{1\cdot(1-\alpha^n)}{1-\alpha}\\\displaystyle=\frac{1-\alpha^n}{1-\alpha}$
あとは、$\displaystyle\alpha=\frac{1+\sqrt3 i}{4}$ を代入してもとに戻していきます。
$\displaystyle\frac{1-\alpha^n}{1-\alpha}\\\displaystyle=\frac{1}{1-\alpha}\cdot(1-\alpha^n)$
分数を代入していくので、いったん分母と分子を分離しておくと計算しやすいでしょう。
$\displaystyle=\frac{1}{1-\frac{1+\sqrt{3}i}{4}}\cdot\left\{\left(1-\frac{1+\sqrt{3}i}{4}\right)^n\right\}$
ここで、
$\displaystyle=\frac{1}{1-\frac{1+\sqrt{3}i}{4}}=\frac{4}{4-(1+\sqrt{3}i)}\\\displaystyle=\frac{4}{3-\sqrt{3}i}=\frac{4(3+\sqrt{3}i)}{9+3}=\frac{3+\sqrt{3}i}{3}$
よって、
$\displaystyle P_n=\frac{3+\sqrt{3}i}{3}\left\{1-\left(\frac{1+\sqrt{3}i}{4}\right)^n\right\}$
(答え)
この問題は、それぞれの直線同士が「長さ半分&60°回転」と一定の関係になっていて、複素数平面ではこれをかけ算で行うことから、等比数列に持ち込めばよいのではないか?と見立てることがポイントです。図形と数列を組み合わせた問題は大事なので色々な問題にチャレンジしましょう。
SNSでシェア