【数Ⅲ複素数平面】入試で問われやすい z+1/z を対処する(2)

前回に引き続き $\displaystyle z+\frac{1}{z}$ の形をやります。今回は複素数を極形式で表したり $x+yi$ で表したりするなど、複素数の様々な表現の方法を学習しましょう。

---

$w$ を $0$ でない複素数、$x$、$y$ を $\displaystyle w+\frac{1}{w}=x+yi$ を満たす実数とする。
(1) 実数 $R$ は $R>1$ を満たす定数とする。$w$ が絶対値 $R$ の複素数全体を動くとき、$xy$ 平面上の点 $(x,y)$ の軌跡を求めよ。
(2) 実数 $\alpha$ は $\displaystyle 0<\alpha<\frac{\pi}{2}$ を満たす定数とする。$w$ が偏角 $\alpha$ の複素数全体を動くとき、$xy$ 平面上の点 $(x,y)$ の軌跡を求めよ。（京都大）

---

極形式を作る

(1) から考えます。複素数平面では複素数の絶対値は原点からの距離を表すのでした。

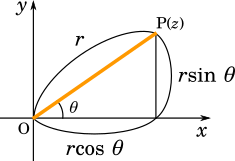
問題文に絶対値が登場するので、極形式で考えると良さそうです。$w$ の絶対値が $R$ ということは、原点からの距離が $R$ であるということです。
$w=R(\cos\theta+i\sin\theta)$
これを問題文の式に代入します。
$\displaystyle w+\frac{1}{w}=R(\cos\theta+i\sin\theta)+\frac{1}{R(\cos\theta+i\sin\theta)}$
分母に $i$ があるときは早めに有理化しておいた方が計算が楽になります。
$\displaystyle =R(\cos\theta+i\sin\theta)+\frac{\cos\theta-i\sin\theta}{R(\cos\theta+i\sin\theta)(\cos\theta-i\sin\theta)}$
$\displaystyle =R(\cos\theta+i\sin\theta)+\frac{\cos\theta-i\sin\theta}{R(\cos^2\theta+\sin^2\theta)}$

よって
$\displaystyle w+\frac{1}{w}=R(\cos\theta+i\sin\theta)+\frac{\cos\theta-i\sin\theta}{R}$
問題文より $\displaystyle w+\frac{1}{w}=x+yi$ だったので、式の実数の部分が $x$ で、虚数の部分が $y$ となります。
$\displaystyle x=R\cos\theta+\frac{\cos\theta}{R}=\left(R+\frac{1}{R}\right)\cos\theta\cdots\text{①}$
$\displaystyle y=R\sin\theta-\frac{\sin\theta}{R}=\left(R-\frac{1}{R}\right)\sin\theta\cdots\text{②}$

解答に近づいてきましたが、 $\theta$ はこちらが勝手に作った文字なので解答には使えません。つまり$\theta$ を消去する必要があります。

よって上の式を変形します。
①より $\displaystyle \cos\theta=\frac{x}{R+\frac{1}{R}}$
②より $\displaystyle \sin\theta=\frac{y}{R-\frac{1}{R}}$
$\sin^2\theta+\cos^2\theta=1$ に当てはめて
$\displaystyle \frac{x^2}{\left(R+\frac{1}{R}\right)^2}+\frac{y^2}{\left(R-\frac{1}{R}\right)^2}=1$ （答え）

偏角を固定する場合

(2) に進みます。偏角が $\alpha$ で固定されていると考えると $w$ は直線であると考えられます。

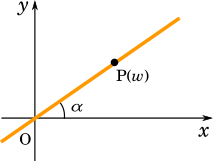
偏角が出てくるのでやはり極形式で考えた方が良さそうです。よって
$w=r(\cos\alpha+i\sin\alpha)$
としておきます。

また、(1)では原点からの距離を $R$ として固定していましたが、今度は偏角を $\alpha$ として固定していて、原点からの距離は固定されてない点にも注意しましょう。

(1) において固定されていた $R$ を固定されていない $r$ に変えて (1) では固定されていなかった $\theta$ を固定された値である $\alpha$ に変えます。
$\displaystyle x=\left(r+\frac{1}{r}\right)\cos\alpha$
$\displaystyle y=\left(r-\frac{1}{r}\right)\sin\alpha$
とします。そして、自分で設定した $r$ は消去しなければなりません。

$\displaystyle x^2=\left(r+\frac{1}{r}\right)^2\cos^2\alpha$
$\displaystyle =\left(r^2+2+\frac{1}{r^2}\right)\cos^2\alpha$
$\displaystyle \frac{x^2}{\cos^2\alpha}=r^2+2+\frac{1}{r^2}\cdots\text{③}$
$\displaystyle y^2=\left(r-\frac{1}{r}\right)^2\sin^2\alpha$
$\displaystyle =\left(r^2-2+\frac{1}{r^2}\right)\sin^2\alpha$
$\displaystyle \frac{y^2}{\sin^2\alpha}=r^2-2+\frac{1}{r^2}\cdots\text{④}$
$r$ を消去します
③－④
$\displaystyle \frac{x^2}{\cos^2\alpha}-\frac{y^2}{\sin^2\alpha}=4$
$\displaystyle \frac{x^2}{(2\cos\alpha)^2}-\frac{y^2}{(2\sin^2\alpha)^2}=1$

これも式変形から初めて分かることです。$w$ が固定された偏角 $\alpha$ の直線上にあるとき、$\displaystyle w+\frac{1}{w}$ は双曲線になるのです。

ここで一応答えは出たのですが、$\displaystyle 0<\alpha<\frac{\pi}{2}$ の条件があったことを思い出しましょう。これに当てはまるように範囲を絞る必要があります。
$\displaystyle x=\left(r+\frac{1}{r}\right)\cos\alpha$
$\displaystyle y=\left(r-\frac{1}{r}\right)\sin\alpha$
から範囲を絞りましょう。
$\displaystyle 0<\alpha<\frac{\pi}{2}$ より
$0<\cos\alpha<1$
$0<\sin\alpha<1$
次に、$\displaystyle r+\frac{1}{r}$と$\displaystyle r-\frac{1}{r}$の範囲も考えます。
$\displaystyle r+\frac{1}{r}$ の範囲から考えます。

$\displaystyle f(r)=r+\frac{1}{r}$ として
$\displaystyle f'(r)=1-\frac{1}{r^2}$
極値を求めます。
$\displaystyle 1-\frac{1}{r^2}=0$ のとき
$r^2-1=0$
$r^2=1$
$r=\pm 1$
ここで $r$ は原点からの距離なのでマイナスの値になることはありません。よって
$r=1$
増減表は

$r$	$\cdots$	1	$\cdots$
$f'(r)$	$-$	0	$+$
$f(r)$		2

最小値は $2$ となるのですが、$\cos$ の最小値が $0$ なので $\displaystyle\left(r+\frac{1}{r}\right)\cos\alpha$ の最小値は結局 $0$ になります。つまり、$x>0$ ということです。

次に $\displaystyle r-\frac{1}{r}$ を考えます。
$\displaystyle g(r)=r-\frac{1}{r}$ として
$\displaystyle g'(r)=1+\frac{1}{r^2}$
極値を求めます。
$\displaystyle 1+\frac{1}{r^2}=0$ のとき
$r^2+1=0$
これは二次関数の解の公式で解きます。
$\displaystyle r=\frac{0\pm\sqrt{0-4}}{2}$
$\displaystyle =\frac{2i}{2}=i$

$\displaystyle r-\frac{1}{r}$ は極値が存在しない単純増加の関数なので範囲も存在しません。つまり、あらゆる値を取りうるということです。よって、$y$ の値に制限はありません。
結果として制限があるのは $x$ の値だけです。よって
$\displaystyle \frac{x^2}{(2\cos\alpha)^2}-\frac{y^2}{(2\sin^2\alpha)^2}=1\enspace(x>0)$ （答え）