【数Ⅲ数列の極限・複素数平面】数列を偶数列と奇数列に分けて考える　階差数列の初項の考え方

このページでマスターしたいこと：偶数列と奇数列で異なる数列になる場合、漸化式から階差数列を求める方法、数列の極限

---

$\alpha$ は $0<|\alpha|<1$ を満たす虚数であるとする。複素数平面上の点の列 $z_1,z_2,z_3,\cdots$ を、
$z_1=0,z_2=1$ および
$\begin{cases}z_{2n+1}-z_{2n}=\alpha(z_{2n}-z_{2n-1})\\z_{2n+2}-z_{2n+1}=\bar \alpha(z_{2n+1}-z_{2n})\end{cases}$
で定める。だたし、虚数とは虚部が $0$ でない複素数のことであり、また、$\bar\alpha$ は $\alpha$ に共役な複素数を表すものとする。このとき以下の問いに答えよ。（岡山大）
(1) 次の等式が成り立つことを示せ。
$z_{2n+2}-z_{2n}=|\alpha|^2(z_{2n}-z_{2n-2})\enspace(n=2,3,4,\cdots)$
(2) 偶数番目の点の列 $z_2,z_4,z_6,\cdots$ および奇数番目の列 $z_1,z_3,z_5,\cdots$ は、それぞれ同一直線上にあることを示せ。
(3) $\displaystyle \lim_{n\rightarrow\infty}|z_n-w|=0$ を満たす複素数 $w$ を求めよ。

---

式同士を足してみる

(1)から取り掛かります。まず問題文の式に番号を振っておきましょう。

$\begin{cases}z_{2n+1}-z_{2n}=\alpha(z_{2n}-z_{2n-1})\cdots\text{①}\\z_{2n+2}-z_{2n+1}=\bar \alpha(z_{2n+1}-z_{2n})\cdots\text{②}\end{cases}$

証明する式から逆算で考えていきます。左辺を見て $z_{2n+1}$ を消したものが証明する式であることに気づくでしょう。そこで
①＋②
$z_{2n+2}-z_{2n}=\alpha(z_{2n}+z_{2n-1})+\bar\alpha(z_{2n+1}-z_{2n})\cdots\text{③}$
今度は右辺を調整します。①と③を見ると $\alpha(z_{2n}-z_{2n-1})$ の部分が共通しています。また、証明する式の右辺に $z_{2n-2}$ があるので、②の式を変形して $z_{2n-2}$ を作ってみます。
$z_{2n}-z_{2n-1}=\bar\alpha(z_{2n-1}-z_{2n-2})\cdots\text{④}$
こうすると、$z_{2n-1}-z_{2n-2}$ の部分が③と共通します。こうやって共通する部分を作ったうえで
①、④を③に代入すると
$z_{2n+2}-z_{2n}=\alpha\bar\alpha(z_{2n-1}-z_{2n-2})+\alpha\bar\alpha(z_{2n}-z_{2n-1})\\=|\alpha|^2(z_{2n}-a_{2n-2})\cdots\text{⑤}$（答え）

階差数列を考える

(2)に進みます。⑤の項は $2n+2,2n,2n-2$ となっていてどれも偶数であることに気づきましょう。ここから偶数の項である $z_2,z_4,z_6,\cdots$ を考えればよいです。

ということは、奇数の項である $z_1,z_3,z_5,\cdots$ の式も必要です。そこで今まで作った式を見て、とりあえず左辺が奇数の項の組み合わせになる式を作れないか考えてみます。

①＋④
$z_{2n+1}-z_{2n-1}=\alpha(z_{2n}-z_{2n+1})+\bar\alpha(z_{2n-1}-z_{2n-2})\cdots\text{⑥}$
左辺が出来たので今度は右辺も奇数の項の式になるように調整します。

①の項数を2減らして
$z_{2n-1}-z_{2n-2}=\alpha(z_{2n-2}-z_{2n-3})\cdots\text{⑦}$
④、⑦を⑥に代入して
$z_{2n+1}-z_{2n-1}=\alpha\bar\alpha(z_{2n-1}-z_{2n-2})+\alpha\bar\alpha(z_{2n-2}-z_{2n-3})\\=|\alpha|^2(z_{2n-1}-z_{2n-3})\cdots\text{⑧}$
これで、奇数の項の式ができました。

⑤の式で考えてみましょう。例えば、$n=2$ なら式は
$z_6-z_4=|\alpha|^2(z_4-z_2)$ となります。これは $z_4$と$z_2$ の差に $|\alpha|^2$ をかけると $z_6$ と $z_4$ の差になるということです。
たとえば、$z_8$ を求めるなら
$z_8=z_2+(z_4-z_2)+(z_4-z_2)|\alpha|^2+(z_4-z_2)|\alpha|^4$
となります。

ここで $|\alpha|^2$ は絶対値なので実数です。$z_4-z_2$ は $z_2$ から $z_4$ に引いた直線のことであり、$z_6-z_4$ は $z_4$ から $z_6$ に引いた直線のことです。問題文より $|\alpha|$が1より小さいなら、$|\alpha|^2$ も1より小さい数になるはずです。そして、$|\alpha|^2$ 倍するということは線の長さが徐々に短くなるということです。

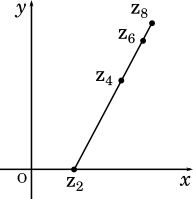
収束の話は(3)で使います。ここでは、一直線になることを証明するのでした。よって、
⑤、⑧より
$z_{2n},z_{2n+1}$ は階差数列であり、項を実数倍したものをその項に加えたものが次の項になるので、一直線である。（答え）

階差数列の初項に注意する

(3)に進みます。

ここから $z_n$ の極値を考えてみます。(2)の問題文より数列を偶数の項と奇数の項で分けて考えると良さそうです。上で解いた問題は次の問題のヒントになることが多いので見逃さないように。

忘れがちですが、階差数列の初項と数列の初項は別です。

このままではらちが明かないのでそれぞれの項を一度計算して、そこから一般項を考えていきましょう。

$z_1=0,z_2=1$
①より
$z_3-z_2=\alpha(z_2-z_1)\\z_3=1+\alpha(1-0)\\z_3=1+\alpha$
②より
$z_4-z_3=|\bar\alpha|(z_3-z_2)$
$z_4=1+\alpha+\bar\alpha(1+\alpha-1)$
$z_4=1+\alpha+|\alpha|^2$
①より
$z_5-z_4=\alpha(z_4-z_3)$
$z_5=1+\alpha+|\alpha|^2+\alpha(1+\alpha+|\alpha|^2-1-\alpha)$
$z_5=1+\alpha+|\alpha|^2(1+\alpha)$
②より
$z_6-z_5=\bar\alpha(z_5-z_4)$
$z_6=1+\alpha+|\alpha|^2(1+\alpha)+\bar\alpha(1+\alpha+|\alpha|^2+\alpha|\alpha|^2-1-\alpha-|\alpha|^2)$
$z_6=1+\alpha+|\alpha|^2+|\alpha|^2(\alpha+|\alpha|^2)$

まずは奇数列の一般項から考えます。各項を並べると

$z_1=0$
$z_3=1+\alpha$
$z_5=1+\alpha+|\alpha|^2(1+\alpha)$

ということで、初項 $1+\alpha$ 公比 $|\alpha|^2$ の極限を考えましょう。

よって、
$\displaystyle\lim_{n\rightarrow\infty} z_{2n+1}=0+\frac{1+\alpha}{1-|\alpha|^2}$
$\displaystyle =\frac{1+\alpha}{1-|\alpha|^2}$
次に偶数列を並べてみると
$z_2=1$
$z_4=1+\alpha+|\alpha|^2$
$z_6=1+\alpha+|\alpha|^2+|\alpha|^2(\alpha+|\alpha|^2)$

よって極限を求めると
$\displaystyle\lim_{n\rightarrow\infty} z_{2n+2}=1+\frac{\alpha+|\alpha|^2}{1-|\alpha|^2}$
$\displaystyle =\frac{1-|\alpha|^2+\alpha+|\alpha|^2}{1-|\alpha|^2}$
$\displaystyle =\frac{1+\alpha}{1-|\alpha|^2}$

よって
$\displaystyle =\frac{1+\alpha}{1-|\alpha|^2}$ （答え）