【数Ⅲ複素数平面】「反対の反対は正しいのだ」の理屈　背理法を用いて値を定める(九州大)

$a$,$b$ を複素数、$c$ を純虚数でない複素数とし、$i$ を虚数単位とする。複素数平面において、点 $z$ が虚軸全体を動くとき
$$\displaystyle w=\frac{az+b}{cz+1}$$
で定まる点 $w$ の軌跡を $C$ とする。次の 3 条件が満たされているとする。
（ア）$z=i$ のときに $w=i$ となり、$z=-i$ のときに $w=-i$ となる。
（イ）$C$ は単位円の周に含まれる。
（ウ）点 $-1$ は $C$ に属さない。
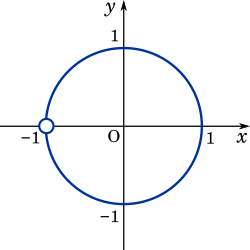
このとき $a,b,c$ の値を求めよ。さらに $C$ を求め、複素数平面上に図示せよ。（九州大2019）

---

条件から 式を作る

まずは条件（ア）は代入するだけなので簡単に式がつくれます。
条件（ア）より
$\displaystyle i=\frac{ia+b}{ic+1}\cdots\text{①}$
$\displaystyle -i=\frac{-ia+b}{-ic+1}\cdots\text{②}$

また、問題文をよく読んでいくつか前提となる式を作っておきます。

まず、 $c$ が純虚数ではないということは $c+\bar c\not =0$
$z$ が虚軸全体を動くということは $z$ は純虚数であるということ
よって　$z+\bar z=0$

（イ）で $C$ が単位円周上を動くということは $|w|=1$

また （ウ）に$-1$ を含まないとあるので $w\not =-1$

①を変形すると
$\displaystyle i=\frac{ia+b}{ic+1}$
$i(ic+1)=ia+b$
$-c+i=ia+b\cdots\text{③}$
②を変形すると
$\displaystyle -i=\frac{-ia+b}{-ic+1}$
$\displaystyle -i(-ic+1)=-ia+b$
$\displaystyle -c-i=-ia+b\cdots\text{④}$
③＋④
$-2c=2b$
$b=-c$
③－④
$2i=2ia$
$a=1$
よって与式は
$\displaystyle w=\frac{z-c}{cz+1}\cdots\text{⑤}$

$z=0$ を代入すると
$\displaystyle w=\frac{-c}{1}$
両辺の絶対値をとって
$|w|=|-c|$

$|w|=|-1|\times|c|$
$|w|=1\times|c|$
$|w|=|c|$

ここで条件（イ）より $|w|=1$ だったので
$|c|=1$

これは言いかえると、複素数 $c$ 全体は原点を中心とする半径 $1$ の円であるということです。しかし、これでは$c$ はいろんな値を取りうるので $1$ つに決めることができません。

$c+\bar c\not =0$ で式を作れそうにないので、$w\not =-1$ で考えてみます。
$w\not =-1$ より
$\displaystyle -1\not =\frac{z-c}{cz+1}$
$-cz-1\not =z-c$
$-cz-z\not =-c+1$
$cz+z\not =c-1$
$(c+1)z\not =c-1$
$\displaystyle z\not =\frac{c-1}{c+1}$

ここで左辺の $z$ は純虚数でした。つまり右辺の $\displaystyle \frac{c-1}{c+1}$ は純虚数になってはいけない、ということです。そうは言っても、右辺が純虚数でないことを検証する方法を考えなければなりません。

そこで複素数を、$c=x+yi$ という形に変換して検証してみます。

また、$c$ は半径 $1$ の円になるので三平方の定理を使って、$x^2+y^2=1$ という関係も作ることができます。

$c=x+yi$ とすると
$\displaystyle z\not =\frac{x-1+yi}{x+1+yi}$
また、$x^2+y^2=1$ より
$y=\sqrt{1-x^2}$
$\displaystyle z\not =\frac{x-1+\sqrt{1-x^2}i}{x+1+\sqrt{1-x^2}i}$

右辺について
$\displaystyle \frac{(x-1+\sqrt{1-x^2}i)(x+1-\sqrt{1-x^2}i)}{(x+1+\sqrt{1-x^2}i)(x+1-\sqrt{1-x^2}i)}$
$\displaystyle =\frac{x^2-1-(x-1)\sqrt{1-x^2}i+(x+1)\sqrt{1-x^2}i+1-x^2}{(x+1)^2+1-x^2}$
$\displaystyle =\frac{(-x+1+x+1)\sqrt{1-x^2}i}{x^2+2x+1+1-x^2}$
$\displaystyle =\frac{2\sqrt{1-x^2}i}{2x+2}$
$\displaystyle =\frac{\sqrt{1-x^2}}{x+1}i$

$x$ が $-1$ 以外のとき、右辺は純虚数となり矛盾する。よって $x=-1$
また、$x^2+y^2=1$ より $y=0$。よって $c=-1$

$c=-1$ のとき $b=1$ である
与式に代入すると
$\displaystyle w=\frac{z+1}{1-z}$
$w(1-z)=z+1$
$w-wz=z+1$
$-wz-z=1-w$
$wz+z=w-1$
$(w+1)z=w-1$
$\displaystyle z=\frac{w-1}{w+1}\enspace(w\not =-1)$

よって
$a=1,b=1,c=-1$　（答え）

$\displaystyle w=\frac{z+1}{1-z}$
$\displaystyle w\bar w=\frac{z+1}{1-z}\cdot\frac{\bar z+1}{1-\bar z}$
$\displaystyle =\frac{z\bar z+z+\bar z+1}{1-\bar z-z+z\bar z}$
条件 $z+\bar z=0$ より
$\displaystyle =\frac{1+z\bar z}{1+z\bar z}=1$
よって
$|w|=1$
また、$z\not =-1$ より、$w$ は原点を中心とする半径 $1$ の円から $w=-1$ を除いた部分。