法線と曲線との交点－始点の座標の置き方を工夫する(横浜国立大2019文系第3問)

実数 $a$ に対し，$xy$ 平面上の曲線 $y=x^3-ax$ を $C$ とする。$C$ 上の異なる 2 点 $\text{P}_1$，$\text{P}_2$ と，2 つの直線 $\ell_1$，$\ell_2$ があり，$k=1,2$ に対して以下の条件をみたしている。

(i) $\text{P}_k$ の $x$ 座標は正である。

(ii) $\ell_k$ は $\text{P}_k$ を通り，さらに $\text{P}_k$ における $C$ の接線と直交する。

(iii) $\ell_k$ は $\text{P}_k$ 以外の点で $C$ と接する。

次の問いに答えよ

(1) $a$ のとる得る値の範囲を求めよ。

(2) $k=1,2$ に対して，$C$ と $\ell_k$ によって囲まれる部分の面積を $S_k$ とする。$S_1+S_2$ を $a$ の式で表せ。

法線が接する点を t とおく

(1)から始めます。

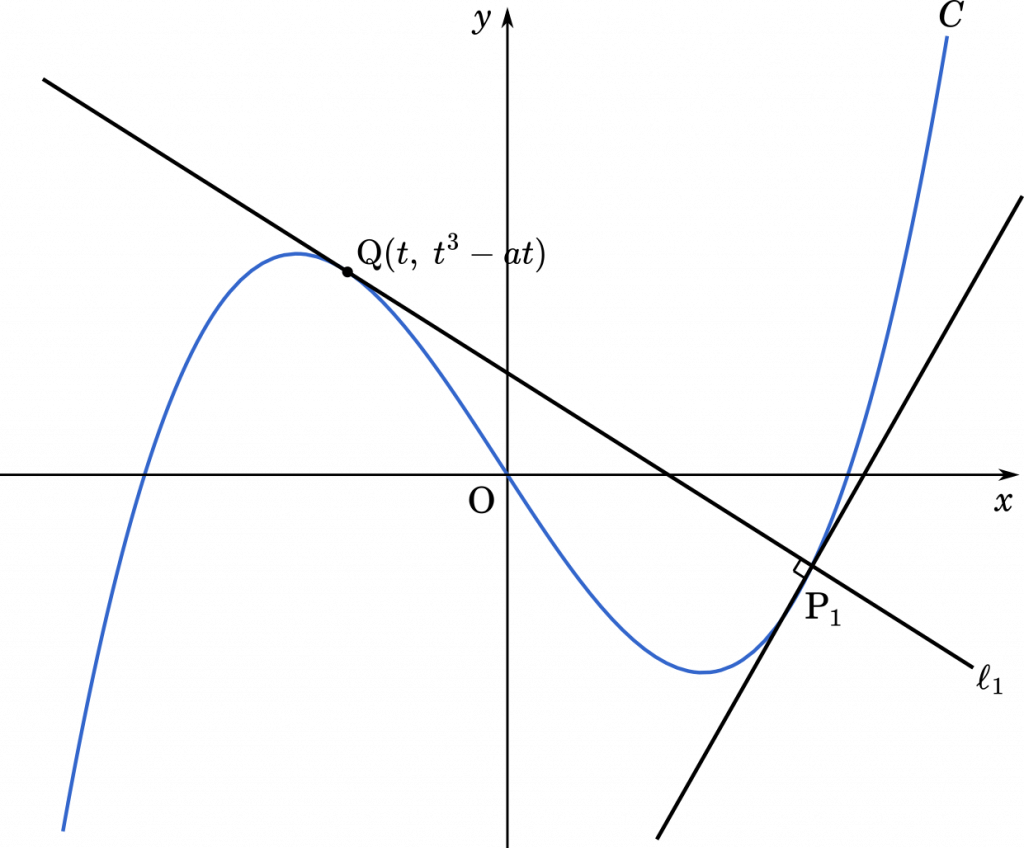
とりあえず，$\text{P}_1$ について考えてみます。

このような問題の場合，一般的には $\text{P}_1$ の $x$ 座標を $t$ とします。しかしながら，これで計算を進めていくとかなりやっかいなことになります（解けないわけではないが一般的にはおそらく解けない）。

そこで，もう一つの手として，$\text{P}_1$ ではない方の接点を $\text{Q}(t,t^3-at)$ として考えてみます。

$y=x^3-ax$ を微分して

$y’=3x^2-a$

Q$(t,t^3-at)$ とすると $x=t$ における接線の傾きは $y’=3t^2-a$ となるので，$\ell_1$ は

$y=(3t^2-a)(x-t)+t^3-at$
$=(3t^2-a)x-3t^3+at+t^3-at$
$=(3t^2-a)x-2t^3$

$C$ と共有点をもつので，式を連立すると

$x^3-ax=(3t^2-a)x-2t^3$
$x^3-3t^2x+2t^3=0$

$\ell_1$ と $C$ は 点Q で共有点をもつので，方程式の解の一つは $x=t$ です。つまり，式は $x-t$ で因数分解できることになります。組立除法を用いて

$\begin{matrix}1&0&-3t^2&2t^3&|\underline{t}\\&t&t^2&-2t^3\\\hline 1&t&-2t^2&0\end{matrix}$

$(x-t)(x^2+tx-2t^2)=0$
$(x-t)(x+2t)(x-t)=0$
$(x-t)^2(x+2t)=0$

よって，もう一つの交点の $x$ 座標は $-2t$ です。

次に，$\text{P}_1$ における $C$ の接線の傾きを求めると

$y’=3(-2t)^2-a$
$=12t^2-a$

となります。$\ell_1$ と $\text{P}_1$ における接線は垂直に交わるので

$(3t^2-a)(12t^2-a)=-1$

の関係が成り立ちます。

展開して整理すると

$36t^4-12at^2-3at^2+a^2+1=0$
$36t^4-15at^2+a^2+1=0$

ここで，$t^2=X$ とすると
$36X^2-15aX+a^2+1=0$

このとき，$X$ は異なる 2 つの正の実数解をもちます。よって，判別式 $D>0$ が成り立ちます。

次に，$D=0$ ではダメなのか，という問題です。このとき $X$ は重解をとります。

たとえば，重解として $X=3$ になったとします。そうすると，$t^2=3$ となり，$t=\pm\sqrt{3}$ となります。

ここで，問題発生です。$\text{P}_1$ の $x$ 座標は $-2t$ ですが，問題文からしてこの値は正の数です。つまり，$t$ は負の数となるので，$t=-\sqrt{3}$ だけが解として適することになります。

問題文からすると，$\text{P}_1$，$\text{P}_2$ が存在する以上，$t$ が一つしか存在しない，というのではつじつまが合いません。$t$ は少なくとも 2 個必要です。

関数が異なる 2 つの正の実数解をもつとき，以下の条件が成り立ちます。これは，基本パターンなので，問題集などで復習しておきましょう。

関数 $f(x)$ が 2 つの正の実数解をもつとき

$\begin{cases}D>0\\\textsf{軸} > 0\\f(0)>0\end{cases}$

$D=225a^2-144(a^2+1)>0$
$81a^2-144>0$
$9a^2-16>0$
$(3a+4)(3a-4)>0$
$a<-\cfrac{4}{3}$，$a>\cfrac{4}{3}$　・・・①

次に，軸は $\cfrac{15}{2}a$ だから

$\cfrac{15}{2}a>0$
$a>0$　・・・②

$f(0)>0$ より

$a^2+1>0$　・・・③

左辺の $a$ にどんな値を代入しても不等式は成り立ちます。つまり，$a$ はすべての実数，となります。

①，②，③より

$a>\cfrac{4}{3}$　（答え）

積分で面積を求める

(2)に進みます。

(1)の結果を用いて，$\ell_1$ と $C$ の共有点の $x$ 座標をそれぞれ $s$，$-2s$，$\ell_2$ と $C$ の共有点の $x$ 座標をそれぞれ $t$，$-2t$ とします。

(1)より $a$ は正の数なので，最初に描いてみたグラフで概形はあっています。積分区間においてグラフの位置関係を考えると，$\ell_1$，$\ell_2$ の方が $C$ より上です。

$\displaystyle S_1=\int_s^{-2s}(3s^2-a)x-2s^3-x^3+ax\space dx$
$\displaystyle =\int_s^{-2s}-x^3+3s^2x-2s^3\space dx$
$=\Big[-\cfrac{x^4}{4}+\cfrac{3}{2}s^2x^2-2s^3x\Big]_s^{-2s}$
$=-4s^4+6s^4+4s^4+\cfrac{s^4}{4}-\cfrac{3}{2}s^4+2s^4$
$=\cfrac{27}{4}s^4$

同様にして

$S_2=\cfrac{27}{4}t^4$

よって

$S_1+S_2=\cfrac{27}{4}(s^4+t^4)$

$36X^2-15aX+a^2+1=0$ の解を $s^2,t^2$ とすると，解と係数の関係より

$s^2+t^2=\cfrac{15}{36}a=\cfrac{5}{12}a$
$s^2t^2=\cfrac{a^2+1}{36}$
$s^4+t^4=(s^2+t^2)^2-2s^2t^2$
$=\cfrac{25}{144}a^2-\cfrac{a^2+1}{18}$
$=\cfrac{17a^2-8}{144}$

したがって

$S_1+S_2=\cfrac{27}{4}\cdot\cfrac{17a^2-8}{144}$
$=\cfrac{51a^2-24}{64}$　（答え）