東京都立大2019理学部第２問　はさみうちの原理と区分求積 |sin nx| の山が並ぶパターン

関数 $f(x)$ は閉区間 $[0,\pi]$ で連続であり、$0\leqq x< y \leqq \pi$ ならばつねに $f(x)\leqq f(y)$ が成り立つとする。以下の問いに答えなさい。（首都大学東京（東京都立大）2019）

(1) 自然数 $n$ に対し、不等式
$$\displaystyle\sum_{k=0}^{n-1} f\left(\frac{\pi}{n}k\right)\int_{\frac{\pi}{n}k}^{\frac{\pi}{n}(k+1)}|\sin nx|dx\leqq\int_0^\pi f(x)|\sin nx|dx\\\leqq\sum_{k=0}^{n-1} f\left(\frac{\pi}{n}(k+1)\right)\int_{\frac{\pi}{n}k}^{\frac{\pi}{n}(k+1)}|\sin nx|dx$$
が成り立つことを示しなさい。
(2) 自然数 $n$ と整数 $k$ に対し、定積分
$$\displaystyle \int_{\frac{\pi}{n}k}^{\frac{\pi}{n}(k+1)}|\sin nx|dx$$
を求めなさい。
(3)$\displaystyle a_n=\int_0^\pi f(x)|\sin nx|dx$
で定まる数列 $\{a_n\}$ が収束することを示しなさい。

---

式変形で証明する

まず、$0\leqq x< y \leqq \pi$ ならばつねに $f(x)\leqq f(y)$ というのは $f(x)$ が単調増加する関数である、という意味です。

ここから $f(x)|\sin nx|$ のグラフをイメージするとこのような感じです。

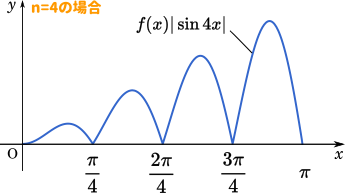
また、不等式の左側の式はグラフで表すと以下のオレンジの部分になります。

右側はこうなります。

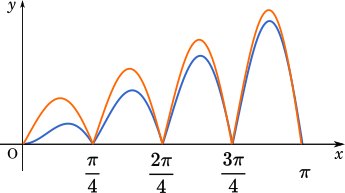
$\sin$ の山の一つについて検討する

まずは式の中で明確に大小関係が言える部分を考えます。そうすると関数 $f(x)$ のカッコの中の部分を使って
$\displaystyle\frac{\pi}{n}k\leqq x\leqq \frac{\pi}{n}(k+1)$
とできます。

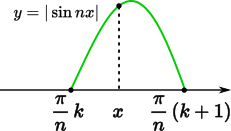
そこから
$\displaystyle f\left(\frac{\pi}{n}k\right)\leqq f(x)\leqq f\left(\frac{\pi}{n}(k+1)\right)$

証明する不等式に近づけていきましょう。今度は $|\sin nx|$ をかけます。
$\displaystyle f\left(\frac{\pi}{n}k\right)|\sin nx|\leqq f(x)|\sin nx|\leqq f\left(\frac{\pi}{n}(k+1)\right)|\sin nx|$
さらに積分してシグマをつけましょう。
$\displaystyle \sum_{k=0}^{n-1}\int_{\frac{\pi}{n}k}^{\frac{\pi}{n}(k+1)} f\left(\frac{\pi}{n}k\right)|\sin nx|dx\leqq \sum_{k=0}^{n-1}\int_{\frac{\pi}{n}k}^{\frac{\pi}{n}(k+1)} f(x)|\sin nx|dx\leqq \sum_{k=0}^{n-1}\int_{\frac{\pi}{n}k}^{\frac{\pi}{n}(k+1)} f\left(\frac{\pi}{n}(k+1)\right)|\sin nx|dx$

ここで $\displaystyle f\left(\frac{\pi}{n}k\right)$ と $\displaystyle f\left(\frac{\pi}{n}(k+1)\right)$ は式の中に $x$ を含まないので定数です。よって、積分の式の外に追い出しましょう。
$\displaystyle \sum_{k=0}^{n-1} f\left(\frac{\pi}{n}k\right) \int_{\frac{\pi}{n}k}^{\frac{\pi}{n}(k+1)} |\sin nx|dx\leqq \sum_{k=0}^{n-1}\int_{\frac{\pi}{n}k}^{\frac{\pi}{n}(k+1)} f(x)|\sin nx|dx\leqq \sum_{k=0}^{n-1} f\left(\frac{\pi}{n}(k+1)\right) \int_{\frac{\pi}{n}k}^{\frac{\pi}{n}(k+1)} |\sin nx|dx$

これで左側と右側はできあがりですが、真ん中の部分を変形する必要があります。
$\displaystyle\sum_{k=0}^{n-1}\int_{\frac{\pi}{n}k}^{\frac{\pi}{n}(k+1)} f(x)|\sin nx|dx$

シグマが $k=0$ から $k=n-1$ までということは
$\displaystyle\int_{0}^{\frac{\pi}{n}} \cdots+\int_{\frac{\pi}{n}}^{\frac{2\pi}{n}} \cdots+\int_{\frac{2\pi}{n}}^{\frac{3\pi}{n}} \cdots+\cdots+\int_{\frac{(n-1)\pi}{n}}^{\pi} \cdots=\int_{0}^{\pi}\cdots$
となるはずです。これで証明完了です。

したがって
$\displaystyle\sum_{k=0}^{n-1} f\left(\frac{\pi}{n}k\right)\int_{\frac{\pi}{n}k}^{\frac{\pi}{n}(k+1)}|\sin nx|dx\leqq\int_0^\pi f(x)|\sin nx|dx\leqq\sum_{k=0}^{n-1} f\left(\frac{\pi}{n}(k+1)\right)\int_{\frac{\pi}{n}k}^{\frac{\pi}{n}(k+1)}|\sin nx|dx$（証明終わり）

(2)

自然数 $n$ と整数 $k$ に対し、定積分
$$\displaystyle \int_{\frac{\pi}{n}k}^{\frac{\pi}{n}(k+1)}|\sin nx|dx$$
を求めなさい。

絶対値の中身によって場合分けする

$\displaystyle \int_{\frac{\pi}{n}k}^{\frac{\pi}{n}(k+1)}|\sin nx|dx$
$x:\frac{\pi}{n}k\rightarrow\frac{\pi}{n}(k+1)$ のとき
$nx:\pi k\rightarrow\pi(k+1)$

よって
(i) $k=2m+1$ のとき $\sin nx\leqq 0$ だから
$\displaystyle \int_{\frac{\pi}{n}(2m+1)}^{\frac{\pi}{n}(2m+2)} -\sin nx dx$
$\displaystyle =\frac{1}{n}[\cos nx]_{\frac{\pi}{n}(2m+1)}^{\frac{\pi}{n}(2m+2)}$
$\displaystyle =\frac{1}{n}\{\cos \pi(2m+2)-\cos \pi(2m+1)\}$

$\displaystyle =\frac{1}{n}(1+1)=\frac{2}{n}$

(ii) $k=2m$ のとき $\sin nx\geqq 0$
$\displaystyle \int_{\frac{2m\pi}{n}}^{\frac{\pi}{n}(2m+1)} \sin nx dx$
$\displaystyle =-\frac{1}{n}[\cos nx]_{\frac{2m\pi}{n}}^{\frac{\pi}{n}(2m+1)}$
$\displaystyle =-\frac{1}{n}\{\cos \pi(2m+1)-\cos 2m\pi\}$

$\displaystyle =-\frac{1}{n}(-1-1)=\frac{2}{n}$
したがって、$\displaystyle \int_{\frac{\pi}{n}k}^{\frac{\pi}{n}(k+1)}|\sin nx|dx=\frac{2}{n}$

(3)

$\displaystyle a_n=\int_0^\pi f(x)|\sin nx|dx$
で定まる数列 $\{a_n\}$ が収束することを示しなさい。

はさみうちの原理を使う

$\displaystyle\sum_{k=0}^{n-1} f\left(\frac{\pi}{n}k\right)\frac{2}{n}\leqq\int_0^\pi f(x)|\sin nx|dx\leqq\sum_{k=0}^{n-1} f\left(\frac{\pi}{n}(k+1)\right)\frac{2}{n}$

左側の式からいきます。
$\displaystyle\sum_{k=0}^{n-1} f\left(\frac{\pi}{n}k\right)\frac{2}{n}$
$\displaystyle \frac{2}{n}$ は定数なので外に追い出します。
$\displaystyle \frac{2}{n}\sum_{k=0}^{n-1} f\left(\frac{\pi}{n}k\right)$

区分求積に持ち込む

ここから極限を考えるのですが、$\displaystyle f\left(\frac{\pi}{n}k\right)$ の中身が分からないのでそのままでは極限の計算はできません。

$\displaystyle \lim_{n\rightarrow\infty} \frac{2}{n}\sum_{k=0}^{n-1} f\left(\frac{\pi}{n}k\right)$

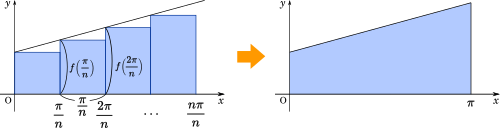
区分求積の考え方は上の図のようになります。関数を長方形の面積の集まりとして表し、長方形の横幅を限りなく細かくしていくと、最終的に関数の積分（面積）になります。

この形に合わせるために、式を細工します。
$\displaystyle \lim_{n\rightarrow\infty} \frac{2}{n}\cdot\frac{n}{\pi}\sum_{k=0}^{n-1} \frac{\pi}{n}f\left(\frac{\pi}{n}k\right)$
$\displaystyle= \frac{2}{\pi}\int_0^\pi f(x)dx$
右辺も同様に
$\displaystyle \frac{2}{\pi}\int_0^\pi f(x)dx$
よって、はさみうちの原理より
$\displaystyle\lim_{n\rightarrow\infty} a_n=\frac{2}{\pi}\int_0^\pi f(x)dx$
したがって、数列$\{a_n\}$ は収束する。