反比例を平行移動したグラフと2次関数の交点，面積(神戸大学2015理系第1問)

座標平面上の 2 つの曲線 $y=\cfrac{x-3}{x-4}$，$y=\cfrac{1}{4}(x-1)(x-3)$ をそれぞ $C_1$，$C_2$ とする。以下の問に答えよ。

(1) 2 曲線 $C_1$，$C_2$ の交点をすべて求めよ。

(2) 2 曲線 $C_1$，$C_2$ の概形をかき，$C_1$ と $C_2$ で囲まれた図形の面積を求めよ。

連立して交点を求める

(1)から始めます。

交点を求めるために，式を連立しましょう。

$\cfrac{x-3}{x-4}=\cfrac{1}{4}(x-1)(x-3)$
$\cfrac{x-3}{x-4}-\cfrac{1}{4}(x-1)(x-3)=0$
$(x-3)\Big\{\cfrac{1}{x-4}-\cfrac{x-1}{4}\Big\}=0$
$(x-3)\cdot\cfrac{4-(x-1)(x-4)}{4(x-4)}=0$
$(x-3)\cdot\cfrac{4-x^2+5x-4}{4(x-4)}=0$
$(x-3)\cdot\cfrac{-x^2+5x}{4(x-4)}=0$
$\cfrac{x(x-3)(x-5)}{x-4}=0$ $(x\not=4)$

$x=0,3,5$

$f(x)=\cfrac{x-3}{x-4}$ とすると

$f(0)=\cfrac{3}{4}$
$f(3)=0$
$f(5)=2$

したがって，交点は $\Big(0,\space\cfrac{3}{4}\Big)$，$(3,0)$，$(5,2)$　（答え）

面積を求める

(2)に進みます。

まずはグラフの概形を描いていきます。

$y=\cfrac{x-3}{x-4}=\cfrac{x-4+1}{x-4}$
$=1+\cfrac{1}{x-4}$

これは，反比例のグラフ $y=\cfrac{1}{x}$ を，$x$ 軸方向に $+4$，$y$ 軸方向に $+1$ 並行移動したグラフです。グラフには漸近線も書き入れましょう。

また，$y=\cfrac{1}{4}(x-1)(x-3)$ は $\cfrac{1}{4}(x-1)(x-3)=0$ とすると，$x=1,3$ が解となるので，下に凸で，$x=1,3$ で $x$ 軸と交わるグラフです。

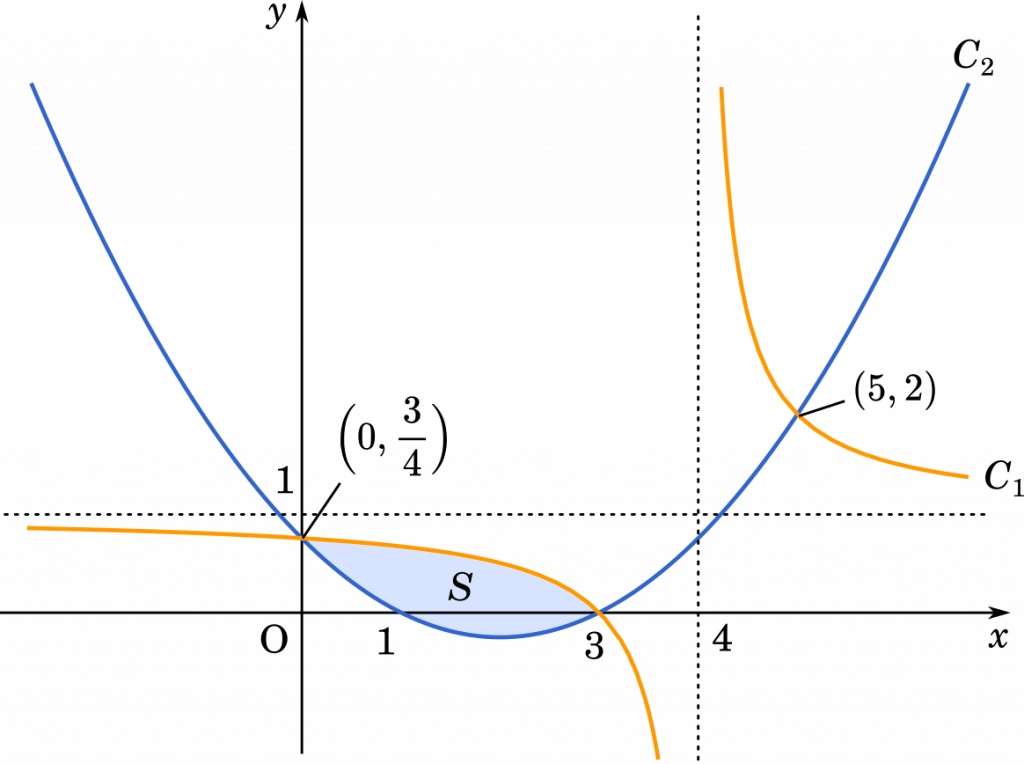
積分区間は $[0,3]$ です。積分していきましょう。

$\displaystyle S=\int_0^3\cfrac{x-3}{x-4}-\cfrac{1}{4}(x-1)(x-3)\space dx$
$\displaystyle S=\int_0^31+\cfrac{1}{x-4}-\cfrac{1}{4}x^2+x-\cfrac{3}{4}\space dx$

公式 $\displaystyle\int\cfrac{1}{x}\space dx=\log |x|+C$ ($C$は積分定数)

$=\Big[\log|x-4|-\cfrac{x^3}{12}+\cfrac{x^2}{2}+\cfrac{1}{4}x\Big]_0^3$
$=\log1-\log4-\cfrac{27}{12}+\cfrac{9}{2}+\cfrac{3}{4}$
$=3-\log 4$　（答え）