外分点のつくりかたで頭ごちゃごちゃになる，をすっきりさせる(東京都立大2016文系第2問)

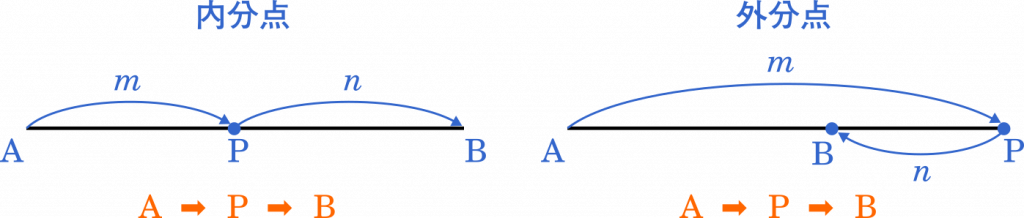
内分点と外分点のとり方は上のようになります。外分点が混乱しがちですが，どちらも A → P → B という道順で進む，と理解しておくと頭の中が整理できると思います。

点の座標は，それぞれ次のようになります。

演習問題

数直線上に 2 点 Q$(-1)$ と $\text{P}_1\Big(\cfrac{1}{2}\Big)$ をとり，線分 $\text{QP}_1$ を $3:1$ に外分する点を $\text{P}_2$，線分 $\text{QP}_2$ を $3:1$ に外分する点を $\text{P}_3$ とする。以下同様に $n=1,2,\cdots$ に対し線分 $\text{QP}_n$ を $3:1$ に外分する点を $\text{P}_{n+1}$ とする。また $\text{P}_n$ の座標を $a_n$ とする。このとき，以下の問いに答えなさい。（東京都立大2016）

(1) A を数直線上の Q と異なる点とする。線分 QA を $3:1$ に外分する点が $\text{P}_1$ であるとき，A の座標 $a$ を求めなさい。

(2) すべての自然数 $n$ に対して
$a_n=\Big(\cfrac{3}{2}\Big)^n-1$
が成り立つことを $n$ に関する数学的帰納法で証明しなさい。

(3) $999<a_n<9999$ をみたす自然数 $n$ をすべて求めなさい。ただし，本問では $\log_{10}2=0.3010$，$\log_{10}3=0.4771$ とする。

外分点の考え方

外分点を理解したところで，(1)から始めましょう。

問題文から，$\text{P}_1$ が外分点になるので，Q → $\text{P}_1$ → A というルートを作りましょう。

これを方程式にすると

$\cfrac{-1(-1)+3a}{3-1}=\cfrac{1}{2}$
$\cfrac{1+3a}{2}=\cfrac{1}{2}$
$1+3a=1$
$3a=0$
$a=0$　（答え）

数学的帰納法

(2)に進みます。

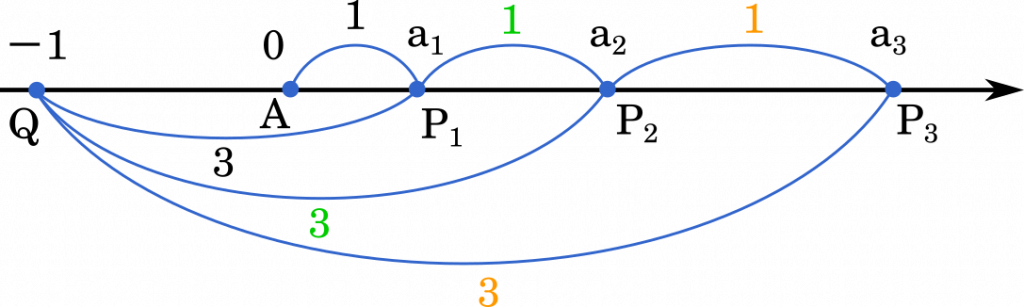
たとえば，外分点 $\text{P}_2$ の座標 $a_2$ を求めるなら
$a_2=\cfrac{-1(-1)+3a_1}{3-1}=\cfrac{1+3a_1}{2}$
となります。同じように $a_3=\cfrac{1+3a_2}{2}$ となるので，結果的に

$a_{n+1}=\cfrac{1+3a_n}{2}$

という式ができます。

これを使って帰納法で式を証明します。

$a_n=\Big(\cfrac{3}{2}\Big)^n-1$ ・・・(*)

とする。

[I] $n=1$ のとき

$a_1=\cfrac{3}{2}-1=\cfrac{1}{2}$

よって，$n=1$ のとき(*)は成り立つ。

[II] $n=k$ として(*)が成り立つと仮定すると，$n=k+1$ のとき

$a_{k+1}=\cfrac{1+3a_k}{2}$
$=\cfrac{3}{2}a_k+\cfrac{1}{2}$
$=\cfrac{3}{2}\Big\{\Big(\cfrac{3}{2}\Big)^k-1\Big\}+\cfrac{1}{2}$
$=\cfrac{3}{2}\Big(\cfrac{3}{2}\Big)^k-\cfrac{3}{2}+\cfrac{1}{2}$
$=\Big(\cfrac{3}{2}\Big)^{k+1}-1$

よって，$n=k+1$ のときも(*)は成り立つ。

[I]，[II]より，すべての自然数 $n$ に対して

$a_n=\Big(\cfrac{3}{2}\Big)^n-1$

が成り立つ。（証明終わり）

対数を用いてけた数を考える

(3)に進みます。ここは問題文から，底を 10 とする対数を作ると良いことが分かります。

たとえば，$\log_{10}100=2$，$\log_{10}1000=3$ となり，3けたの数なら 2，4けたの数なら 3 というように，けた数より 1 小さい数が求められます。これを利用していきます。

$\log_{10}\Big(\cfrac{3}{2}\Big)^n$ とすると

$=n\log_{10}\cfrac{3}{2}$
$=n(\log_{10}3-\log_{10}2)$
$=n(0.4771-0.3010)$
$=0.1761n$

よって

$999<a_n<9999$
$999<\Big(\cfrac{3}{2}\Big)^n-1<9999$
$1000<\Big(\cfrac{3}{2}\Big)^n<10000$
$\log_{10}1000<\log_{10}\Big(\cfrac{3}{2}\Big)^n<\log_{10}10000$
$3<0.1761n<4$

ここで，$3<0.1761n$ は

$17.\cdots<n$

$n$ は自然数より

$17<n$

また，$0.1761n<4$ は

$n<22.\cdots$
$n\leqq22$

まとめると

$17<n\leqq22$

したがって

$n=18,19,20,21,22$　（答え）