【数Ⅲ極限】図形と数列の極限　三角形が無限増殖するフラクタル(北海道大2010後期)

1辺の長さが $1$ の正三角形 $D_0$ から出発して、多角形 $D_1$、$D_2$、…、$D_n$、…を次のように定める。
(i) $AB$ を $ D_{n-1}$ の1辺とする。辺 $AB$を3等分し、その分点を$A$に近い方から$P$，$Q$とする。
(ii) $PQ$を1辺とする正三角形 $PQR$ を $D_{n-1}$ の外側に作る。
(iii) 辺 $AB$を折れ線 $APRQB$ で置き換える。$D_{n-1}$ のすべての辺に対して(i)～(iii)の操作を行って得られる多角形を$D_n$とする。
以下の問いに答えよ。
(1) $D_n$ の周の長さ $L_n$ を $n$ で表せ。
(2) $D_n$ の面積を$n$で表せ。
(3) $\displaystyle\lim_{n\rightarrow\text{∞}} S_n$ を求めよ。（北海道大2010後期・改)

---

周の長さを求める

まずは、周の長さ $L_n$ を求めます。

(i) ～ (iii) の操作を図にするとこのような感じです。

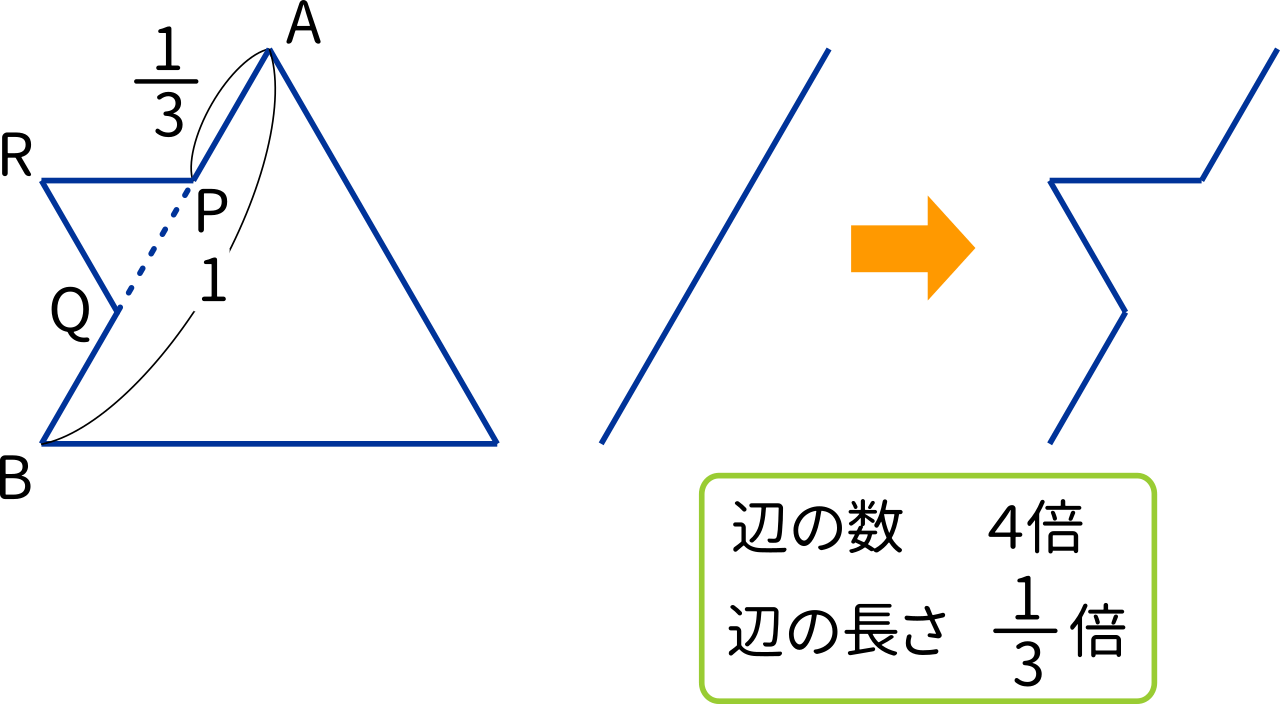
正三角形の一片に新たな正三角形をくっつけていくわけです。このとき、いったん辺の数を考えてみます。そうすると、もともと $1$ つの辺が $4$ つに増えているのが分かります。これが全ての辺で起こるので、もとの辺の数を $4$ 倍すれば次の図形の辺の数になります。辺の数は $D_0$ のとき $3$ で、そこから $3\times 4$、$3\times 4\times 4$、…となり、$3\cdot 4^n$ で表せます。

辺の数が分かったので、ここから周の長さを考えます。これは、周の長さ＝辺の長さ×辺の数、という計算になります。

辺の長さは $D_0$ のとき $1$ で、そこから $\displaystyle\frac{1}{3}$、$\displaystyle\frac{1}{3}\times\frac{1}{3}$、…となり、$\displaystyle\left(\frac{1}{3}\right)^n$ でいけそうです。

つまり

$\displaystyle L_n=\left(\frac{1}{3}\right)^n\cdot3\cdot4^n\\\displaystyle=3\left(\frac{4}{3}\right)^n$

(答え)

面積を求める

次に面積を求めます。

もとの三角形に新しい三角形がくっついていくので、ひたすら面積が増えていくことになります。そこで、新たにくっつく三角形の面積を考えていきます。

正三角形の角の大きさは $60$°より

$\displaystyle\frac{1}{2}\cdot1\cdot1\cdot\sin 60\text{°}=\frac{1}{2}\cdot\frac{\sqrt{3}}{2}=\frac{\sqrt{3}}{4}$

そして次の図形では、もとの辺の長さを $\displaystyle\frac{1}{3}$ にした三角形を辺の数だけくっつけていきます。

ここから、新しい三角形の面積は、もとの三角形の面積に面積 $\displaystyle\frac{1}{9}$ 倍の三角形を辺の数だけ加えたもの、となります。

よって、新しくくっつける三角形の面積は $\displaystyle\frac{\sqrt{3}}{4}\left(\frac{1}{9}\right)^n$ となります。

また、辺の数は先ほど求めた $3\cdot4^n$ ですが、たとえば $n=1$ のときは、一つ前の $n=0$ の図形の辺に新しい三角形を加えていくので、$3\cdot4^{n-1}$ で考えないといけない点に注意しましょう。

よって

$\displaystyle S_n=S_{n-1}+\frac{\sqrt{3}}{4}\left(\frac{1}{9}\right)^n\cdot3\cdot4^{n-1}$

いったん、$\displaystyle b_n=\frac{\sqrt{3}}{4}\left(\frac{1}{9}\right)^n\cdot3\cdot4^{n-1}$ として考えると、

$S_n=S_{n-1}+b_n$

つまり

$S_1=S_0+b_1\\S_2=\color{blue}{S_1}+b_2=\color{blue}{S_0+b_1}+b_2\\S_3=\color{blue}{S_2}+b_3\\=\color{blue}{S_0+b_1+b_2}+b_3$

となります。

そこで、$\displaystyle\frac{\sqrt{3}}{4}\left(\frac{1}{9}\right)^n\cdot3\cdot4^{n-1}$ の和を考えます。

$\displaystyle\frac{\sqrt{3}}{4}\left(\frac{1}{9}\right)^n\cdot3\cdot4^{n-1}\\\displaystyle=\frac{\sqrt{3}}{4}\left(\frac{1}{9}\right)^{n-1}\cdot\frac{1}{9}\cdot3\cdot4^{n-1}\\\displaystyle=\frac{\sqrt{3}}{12}\left(\frac{4}{9}\right)^{n-1}$

よって、等比数列の和の公式を使って数列の和を求めると

$\displaystyle\frac{\frac{\sqrt{3}}{12}\left\{1-\left(\frac{4}{9}\right)^n\right\}}{1-\frac{4}{9}}\\\displaystyle=\frac{\sqrt{3}}{12}\cdot\frac{1-\left(\frac{4}{9}\right)^n}{\frac{5}{9}}\\\displaystyle=\frac{\sqrt{3}}{12}\cdot\frac{9}{5}\left\{1-\left(\frac{4}{9}\right)^n\right\}\\\displaystyle=\frac{3\sqrt{3}}{20}\left\{1-\left(\frac{4}{9}\right)^n\right\}$

ここで、 $S_n=S_0+$数列の和　だったので

$\displaystyle S_n=\frac{\sqrt{3}}{4}+\frac{3\sqrt{3}}{20}\left\{1-\left(\frac{4}{9}\right)^n\right\}\\\displaystyle=\frac{\sqrt{3}}{4}+\frac{3\sqrt{3}}{20}-\frac{3\sqrt{3}}{20}\left(\frac{4}{9}\right)^n\\\displaystyle=\frac{5\sqrt{3}}{20}+\frac{3\sqrt{3}}{20}-\frac{3\sqrt{3}}{20}\left(\frac{4}{9}\right)^n\\\displaystyle=\frac{8\sqrt{3}}{20}-\frac{3\sqrt{3}}{20}\left(\frac{4}{9}\right)^n\\\displaystyle=\frac{2\sqrt{3}}{5}-\frac{3\sqrt{3}}{20}\left(\frac{4}{9}\right)^n$

(答え)

極限を求める

$\displaystyle\lim_{n\rightarrow\text{∞}} S_n\\\displaystyle=\lim_{n\rightarrow\text{∞}}\frac{2\sqrt{3}}{5}-\frac{3\sqrt{3}}{20}\left(\frac{4}{9}\right)^n$

ここで、$\displaystyle\left(\frac{4}{9}\right)^n$ は $n\rightarrow\text{∞}$ とすると $0$ に収束するので

$\displaystyle\lim_{n\rightarrow\text{∞}}\frac{2\sqrt{3}}{5}-\frac{3\sqrt{3}}{20}\left(\frac{4}{9}\right)^n\\=\displaystyle\frac{2\sqrt{3}}{5}-0\\\displaystyle=\frac{2\sqrt{3}}{5}$

(答え)