【数Ⅲ複素数平面】Zの表す図形が垂直二等分線、円になる（国公立基本レベル）

2つの複素数 $w,z$ が $\displaystyle w=\frac{iz}{z-2}$ を満たしているとする。ただし、$i$ は虚数単位とする。次の問いに答えよ。（弘前大）
(1) 複素数平面上で、点 $z$ が原点を中心とする半径2の円周上を動くとき、点 $w$ はどのような図形を描くか。ただし、$z\not =2$ とする。
(2) 複素数平面上で点 $z$ が虚軸上を動くとき、点 $w$ はどのような図形を描くか。
(3) 複素数平面上で点 $w$ が実軸上を動くとき、点 $z$ はどのような図形を描くか。

---

垂直二等分線

(1)を考えます。まず複素数zが円になることから、原点を中心とする半径2の円は$|z|=2$ と表すことができます。

これを使って式をz=の式に変形していきます。

$\displaystyle w=\frac{iz}{z-2}\\\displaystyle(z-2)w=iz\\wz-2w-iz=0\\wz-iz=2w\\z(w-i)=2w\\\displaystyle z=\frac{2w}{w-i}$

$\displaystyle |z|=\left|\frac{2w}{w-i}\right|$

よって
$\displaystyle 2=\frac{|2w|}{|w-i|}\\2|w-i|=|2w|\\2|w-i|=2|w|\\|w-i|=|w|$

こうして出来上がった $|w-i|=|w|$ は $|w-i|=|w-0|$ ということだから、垂直二等分線の形になっています。
よって、$w$ は $ 0,i$ の垂直二等分線（答え）

zが純虚数

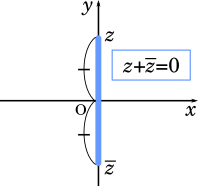
(2)に進みます。zが純虚数であるということは $z+\bar z=0$ の関係が成り立つということです。純虚数とは $2i$ のような数で、実部がなくて虚部だけの数のことです。$2i$ の共役な複素数は $-2i$ だから、$2i-2i=0$ が成り立ちます。

$\displaystyle z=\frac{2w}{w-i}(w\not =i)\cdots\text{①}$ より
$\displaystyle \bar z=\left(\overline{\frac{2w}{w-i}}\right)=\frac{2\bar w}{\bar w+i}\cdots\text{②}$

①＋②より
$\displaystyle z+\bar z=\frac{2w}{w-i}+\frac{2\bar w}{\bar w+i}=0\\\displaystyle \frac{2w}{w-i}=-\frac{2\bar w}{\bar w+i}\\\displaystyle\frac{w}{w-i}=-\frac{\bar w}{\bar w+i}\\w(\bar w+i)=-\bar w(w-i)\\w\bar w+iw=-w\bar w+i\bar w\\2w\bar w+iw-i\bar w=0$

ここで、$(w+a)(\bar w+b)=w\bar w+bw+a\bar w+ab$ より
$(w+a)(\bar w+b)=w\bar w+bw+a\bar w+ab\\w\bar w+bw+a\bar w=(w+a)(\bar w+b)-ab$ が成り立ちます。式を変形すると
$2w\bar w+iw-i\bar w=0\\\displaystyle w\bar w+\frac{1}{2}iw-\frac{1}{2}i\bar w=0\\\displaystyle \left(w-\frac{1}{2}i\right)\left(\bar w+\frac{1}{2}i\right)-\frac{1}{4}=0\\\displaystyle\left(w-\frac{1}{2}i\right)\left(\overline{w-\frac{1}{2}i}\right)=\frac{1}{4}$
ここで公式 $z\bar z=|z|^2$ より
$\displaystyle\left|w-\frac{1}{2}i\right|^2=\frac{1}{4}\\\displaystyle\left|w-\frac{1}{2}i\right|=\frac{1}{2}$
これは円の形です。よって
$\displaystyle\frac{i}{2}$ を中心とする半径$\displaystyle\frac{1}{2}$ の円（ただし、$i$を除く）。（答え）

wが実数

(3)に進みます。wが実数であるということは $w=\bar w$ の関係が成り立つということです。実数というのは虚部が0ということだから、たとえば $2+0i=2-0i$ とすると、左右でイコール関係が成り立ちます。これを使って式を作っていきましょう。

$\displaystyle w=\frac{iz}{z-2}$ より
$\displaystyle \frac{iz}{z-2}=\left(\overline{\frac{iz}{z-2}}\right)\\\displaystyle \frac{iz}{z-2}=\frac{-i\bar z}{\bar z-2}\\\displaystyle \frac{z}{z-2}=-\frac{\bar z}{\bar z-2}\\z(\bar z-2)=-\bar z(z-2)\\z\bar z-2z=-z\bar z+2\bar z\\2z\bar z-2z-2\bar z=0\\z\bar z-z-\bar z=0$

$(z-1)(\bar z-1)-1=0$
$(z-1)(\bar z-1)=1$
ここで、公式$z\bar z=|z|^2$ より
$|z-1|^2=1\\|z-1|=1$
これは円の形になります。よって
1を中心とする半径1の円（ただし2を除く）（答え）

基本的な問題ですが、実数や純虚数の定義など忘れやすい部分なのでしっかり覚えましょう。