【数Ⅲ複素数平面】入試で問われやすい z+1/z を対処する

複素数平面の実際の入試問題はパターンで対処できないことが多いのですが、比較的出されやすい $\displaystyle z+\frac{1}{z}$ の対処法をここで紹介します。

---

(1) $\displaystyle z+\frac{1}{z}=\sqrt{3}$ を満たす複素数 $z$ の値を求めよ。また、このとき $\displaystyle \alpha=z^{100}+\frac{1}{z^{100}}$ の値を求めよ。
(2) $\displaystyle z+\frac{1}{z}$ が実数となるような複素数 $z$ が表す複素数平面上の点全体は、どのような図形を表すか。
(3) $\displaystyle z+\frac{1}{z}$ が実数となる複素数 $z$ と、$\displaystyle \left|w-\left(\frac{8}{3}+2i\right)\right|=\frac{2}{3}$ を満たす複素数 $w$ について、$|z-w|$ の最小値を求めよ。（名古屋工業大）

ド・モアブルを使う

(1) から考えます。$\displaystyle z+\frac{1}{z}=\sqrt{3}$ は普通に方程式と考えて解いてしまいます。
$\displaystyle z+\frac{1}{z}=\sqrt{3}$
全体に$\times z$ をして
$\displaystyle z^2+1=\sqrt{3}z$
$z^2-\sqrt{3}z+1=0$
$\displaystyle z=\frac{\sqrt{3}\pm\sqrt{3-4}}{2}$
$\displaystyle =\frac{\sqrt{3}\pm i}{2}$
$\displaystyle =\frac{\sqrt{3}}{2}\pm \frac{1}{2}i$　（答え）

次に $\displaystyle \alpha=z^{100}+\frac{1}{z^{100}}$ を求めます。
まずは、$z^{100}$ を求めるのですが、こうやって指数に大きな数がきたらド・モアブルの定理です。

ド・モアブルの定理を使うために、複素数を極形式に直しましょう。
$\displaystyle z=\frac{\sqrt{3}}{2}\pm \frac{1}{2}i$
$\displaystyle =\cos\frac{\pi}{6}\pm i\sin\frac{\pi}{6}$
よって
$\displaystyle z^{100}=\left(\cos\frac{\pi}{6}\pm i\sin\frac{\pi}{6}\right)^{100}$
$\displaystyle =\cos\frac{100}{6}\pi\pm i\sin\frac{100}{6}\pi$

$\displaystyle \frac{100}{6}=\frac{50}{3}$ としてその中から $2\pi$ のかたまりを取り除きます。

$50=6\times 8+2$ だから、$\displaystyle\cos\frac{50}{3}\pi=\cos\frac{2}{3}\pi$
よって
$\displaystyle z^{100}=\cos\frac{2}{3}\pi\pm i\sin\frac{2}{3}\pi$
$\displaystyle =-\frac{1}{2}\pm \frac{3}{2}i$
となる。これを $\displaystyle \alpha=z^{100}+\frac{1}{z^{100}}$ に代入します。

ただ $\pm$ をそのまま代入すると計算ミスが怖いので、今回は分けて計算します。
$[1] +$ の場合
$\displaystyle =-\frac{1}{2}+\frac{\sqrt{3}}{2}+\frac{1}{-\frac{1}{2}+\frac{\sqrt{3}}{2}i}$
$\displaystyle =\frac{\left(-\frac{1}{2}+\frac{\sqrt{3}}{2}i\right)^2+1}{-\frac{1}{2}+\frac{\sqrt{3}}{2}i}$
$\displaystyle =\frac{\frac{1}{2}-\frac{\sqrt{3}}{2}i}{-\frac{1}{2}+\frac{\sqrt{3}}{2}i}=\frac{1-\sqrt{3}i}{-1+\sqrt{3}i}$
分母に $i$ があるので分母の有理化をしていきます。
$\displaystyle =\frac{(1-\sqrt{3}i)(-1-\sqrt{3}i)}{(-1+\sqrt{3}i)(-1-\sqrt{3}i)}$
$\displaystyle =\frac{-1-\sqrt{3}i+\sqrt{3}i-3}{1+3}=-1$

$[2] -$ の場合
$\displaystyle =-\frac{1}{2}-\frac{\sqrt{3}}{2}+\frac{1}{-\frac{1}{2}-\frac{\sqrt{3}}{2}i}$

$=-1$
どちらも $-1$ となるので、 $\displaystyle \alpha=z^{100}+\frac{1}{z^{100}}=-1$（答え）

実数の条件から図形を描く

(2) に進みます。

問題文に実数とあることから、複素数が実数になる条件を思い出しましょう。

この条件を問題文の式に当てはめると
$\displaystyle z+\frac{1}{z}=\bar{z}+\frac{1}{\bar z}\enspace(z\not =0)$
$\displaystyle z-\bar z-+\frac{1}{z}-\frac{1}{\bar z}=0$
$\displaystyle z-\bar z+\frac{\bar z-z}{z\bar z}=0$
$\displaystyle z-\bar z-\frac{z-\bar z}{z\bar z}=0$
全体に $z\bar z$ をかけて
$(z-\bar z)z\bar z-(z-\bar z)=0$
$(z-\bar z)(z\bar z-1)=0$

ここで $=0$ が成り立つのは
$z-\bar z=0$ または $z\bar z-1=0$ のときです。
よって
$z=\bar z$ または $|z|^2=1$
$z=\bar z$ は $z$ が実数であるということで、どんな実数でも成り立ちます。つまり、実数全体です。従って
すべての実数と原点を中心とする半径 $1$ の円。(ただし原点を除く）（答え）

図を描いて解決する

(3) は図を描けば案外あっさり終わります。

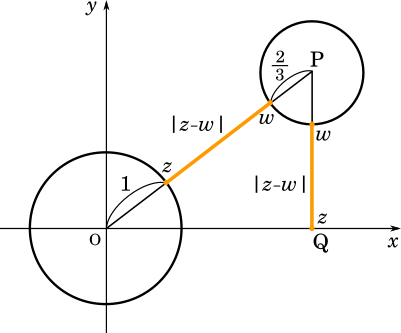
先ほどの (2) から $z$ は原点中心の半径 $1$ の円か実軸上でした。まず、$z$ が円上の点である場合から考えます。

問題文より、$w$ は $\displaystyle \left(\frac{8}{3},2\right)$ を中心とする半径 $\displaystyle \frac{2}{3}$ の円の上にあります。そして $|z-w|$ は $z$ と $w$ の間の距離で、要するにその最短距離を求めようということです。

そして、最短距離は上の図で示した通り、原点から $w$ の描く円の中心$P$に引っぱった直線上になります。まずは、三平方の定理を使って直線$OP$の長さを求めましょう。

$\displaystyle OP=\sqrt{\left(\frac{8}{3}\right)^2+2^2}$
$\displaystyle OP=\sqrt{\left(\frac{8}{3}\right)^2+2^2}=\sqrt{\frac{100}{9}}$
$\displaystyle =\frac{10}{3}$
ここから円の半径を引きます
$\displaystyle \frac{10}{3}-1-\frac{2}{3}=\frac{5}{3}\cdots\text{①}$

次に $z$ が実軸上である場合を考えると今度は $PQ$ から円の半径を引けば良さそうです。
$\displaystyle 2-\frac{2}{3}=\frac{4}{3}\cdots\text{②}$
①、②を比べて最小値は $\displaystyle\frac{4}{3}$ （答え）