e^xsin^2x の積分：セオリーを身につける(横浜国立大2019理系第5問)

2 つの関数 $f(x)=e^{-x}\sin x\space(0\leqq x\leqq2\pi)$ と $g(x)=-e^{^x}\space(0\leqq x\leqq2\pi)$ について，次の問いに答えよ。

(1) $f(x)$ が最小値をとるときの $x$ の値を求めよ。

(2) $f(x)=g(x)$ をみたす $x$ の値を求めよ。

(3) 2 曲線 $C_1:y=f(x)$，$C_2:y=g(x)$ と $y$ 軸で囲まれる部分を，$x$ 軸のまわりに 1 回転してできる立体の体積 $V$ を求めよ。

微分と合成関数

(1)から始めます。

$e^x\sin x$ の形は定番ともいえるパターンなので，練習しておいた方が良いでしょう。今回は少しひねりが入っていますが，基本的な考え方は同じです。

まずは，微分して極値を求めていきましょう。

$f'(x)=-e^{-x}\sin x+e^{-x}\cos x$

$-e^{-x}\sin x+e^{-x}\cos x=0$ として

$-e^{-x}(\sin x-\cos x)=0$

$e^{-x}\not=0$ だから，$\sin x-\cos x=0$

合成関数を用いて

$\sqrt{2}\sin\Big(x-\cfrac{\pi}{4}\Big)=0$
$x-\cfrac{\pi}{4}=0,\pi$
$x=\cfrac{\pi}{4},\space\cfrac{5}{4}\pi$

$\def\arraystretch{1.5}\begin{array}{|c|c|c|c|c|c|c|c|}\hline x&0&\cdots&\frac{\pi}{4}&\cdots&\frac{5\pi}{4}&\cdots&2\pi\\\hline f'(x)&+&+&0&-&0&+&+\\\hline f(x)&0&\nearrow&&\searrow&&\nearrow&0\\\hline\end{array}$

$f\Big(\cfrac{\pi}{4}\Big)=e^{\small{-\frac{\pi}{4}}}\sin\cfrac{\pi}{4}=\cfrac{e^{\small{-\frac{\pi}{4}}}}{\sqrt{2}}$

$f\Big(\cfrac{5\pi}{4}\Big)=e^{\small{-\frac{5\pi}{4}}}\sin\cfrac{5}{4}\pi=-\cfrac{e^{\small{-\frac{5\pi}{4}}}}{\sqrt{2}}$

したがって

$x=\cfrac{5\pi}{4}$ のとき，最小値 $-\cfrac{e^{\small{-\frac{5\pi}{4}}}}{\sqrt{2}}$　（答え）

f(x)=g(x)を求める

(2)に進みます。

$e^{-x}\sin x=-e^{-x}$
$e^{-x}\sin x+e^{-x}=0$
$e^{-x}(\sin x+1)=0$

$e^{-x}\not=0$ だから $\sin x+1=0$

$\sin x=-1$
$x=\cfrac{3}{2}\pi$　（答え）

回転体の体積

(3)に進みます。

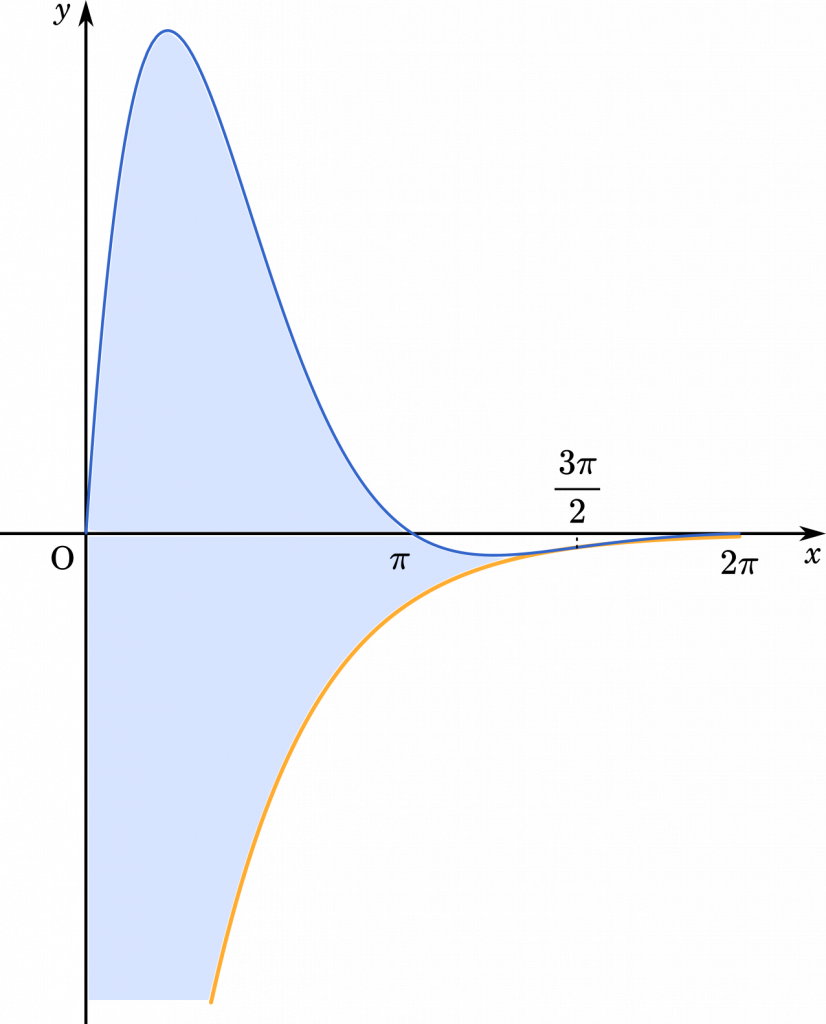
回転体の体積を考えていきますが，ここはグラフの概形があった方が良いでしょう。

まず $f(x)=g(x)$ となるのは，(2)より $x=\cfrac{3}{2}\pi$ のときだから，積分区間は $\Big[0,\cfrac{3\pi}{2}\Big]$ です。

また，$e^{-x}$ は $x$ が正の値でも負の値でも必ず正の値になることに注意しましょう。

$e^{-x}>0$

よって，$f(x)$ と $g(x)$ の関係は

(i) $0\leqq x\leqq\pi$ のとき

$0\leqq\sin x\leqq1$ だから

$|e^{-x}\sin x|\leqq |-e^{-x}|$

(ii) $\pi<x\leqq\cfrac{3\pi}{2}$ のとき

$-1\leqq\sin x\leqq0$ だから

$|e^{-x}\sin x|\leqq |-e^{-x}|$

回転体の体積は円の面積を積分で積み重ねることで求めます。つまり，$\pi r^2$ の積分ということです。

$\displaystyle V=\pi\int_0^\pi (e^{-x})^2\space dx+\pi\int_\pi^{\small{\frac{3\pi}{2}}}(e^{-x})^2-(e^{-x}\sin x)^2\space dx$
$\displaystyle=\pi\int_0^{\small{\frac{3\pi}{2}}}(e^{-x})^2\space dx-\pi\int_\pi^{\small{\frac{3\pi}{2}}}(e^{-x}\sin x)^2\space dx$
$\displaystyle=\pi\int_0^{\small{\frac{3\pi}{2}}}e^{-2x}\space dx-\pi\int_\pi^{\small{\frac{3\pi}{2}}}e^{-2x}\sin^2 x\space dx$

$\sin^2x$ や $\cos^2x$ がきたら，半角の公式を使うのがセオリーです。

$\displaystyle=\pi\int_0^{\small{\frac{3\pi}{2}}}e^{-2x}\space dx-\pi\int_\pi^{\small{\frac{3\pi}{2}}}e^{-2x}\cdot\cfrac{1-\cos2x}{2}\space dx$
$\displaystyle=\pi\int_0^{\small{\frac{3\pi}{2}}}e^{-2x}\space dx-\cfrac{\pi}{2}\int_\pi^{\small{\frac{3\pi}{2}}}e^{-2x}\space dx+\cfrac{\pi}{2}\int_\pi^{\small{\frac{3\pi}{2}}}e^{-2x}\cos2x\space dx$

それぞれの積分について計算してみます。

$\displaystyle\pi\int_0^{\small{\frac{3\pi}{2}}}e^{-2x}\space dx$
$=-\cfrac{\pi}{2}\Big[e^{-2x}\Big]_0^{\small{\frac{3\pi}{2}}}$
$=-\cfrac{\pi}{2}(e^{-3\pi}-1)$
$=\cfrac{\pi}{2}(1-e^{-3\pi})$　・・・①

$\displaystyle\cfrac{\pi}{2}\int_\pi^{\small{\frac{3\pi}{2}}}e^{-2x}\space dx$
$=-\cfrac{\pi}{4}\Big[e^{-2x}\Big]_\pi^{\small{\frac{3\pi}{2}}}$
$=-\cfrac{\pi}{4}(e^{-3\pi}-e^{-2\pi})$
$=\cfrac{\pi}{4}(e^{-2\pi}-e^{-3\pi})$　・・・②

$\displaystyle\cfrac{\pi}{2}\int_\pi^{\small{\frac{3\pi}{2}}}e^{-2x}\cos2x\space dx$

$e^x\sin x$ のような形が来たら，とりあえず $\sin x$ と $\cos x$ のセットで微分してみるとうまくいきます。この辺りもセオリーなので暗記しましょう。

$(e^{-2x}\sin 2x)’=-2e^{-2x}\sin2x+2e^{-2x}\cos2x$
$(e^{-2x}\cos 2x)’=-2e^{-2x}\cos2x-2e^{-2x}\sin2x$

上の式から下の式を引いて，$\sin$ を消去します。

$\{e^{-2x}(\sin2x-\cos2x)\}’=4e^{-2x}\cos2x$
$\cfrac{1}{4}\{e^{-2x}(\sin2x-\cos2x)\}’=e^{-2x}\cos2x$

よって

$=\cfrac{\pi}{2}\cdot\cfrac{1}{4}\Big[e^{-2x}(\sin2x-\cos2x)\Big]_\pi^{\small{\frac{3\pi}{2}}}$
$=\cfrac{\pi}{8}\{e^{-3\pi}(\sin3\pi-\cos3\pi)-e^{-2\pi}(\sin2\pi-\cos2\pi)\}$
$=\cfrac{\pi}{8}\{e^{-3\pi}(0+1)-e^{-2\pi}(0-1)\}$
$=\cfrac{\pi}{8}(e^{-3\pi}+e^{-2\pi})$　・・・③

①－②＋③

$V=\cfrac{\pi}{2}(1-e^{-3\pi})-\cfrac{\pi}{4}(e^{-2\pi}-e^{-3\pi})+\cfrac{\pi}{8}(e^{-3\pi}+e^{-2\pi})$
$=\cfrac{\pi}{8}(4-4e^{-3\pi}-2e^{-2\pi}+2e^{-3\pi}+e^{-3\pi}+e^{-2\pi})$
$=\cfrac{\pi}{8}(4-e^{-3\pi}-e^{-2\pi})$　（答え）