【III極限・積分】e^x cos x を積分する方法（覚えたらカンタン）(東京都立大2015理学部第1問)

以下の問いに答えなさい。（東京都立大2015）

(1) 次の不定積分を求めなさい。

$\displaystyle\int e^{-2x}\cos 2x\space dx$

(2) $n$ を正の整数とする。曲線

$y=e^{-x}\sin x$　$((n-1)\pi\leqq x\leqq n\pi)$

と $x$ 軸で囲まれる部分を $x$ 軸の周りに 1 回転させてできる立体の体積 $V_n$ を求めなさい。

(3) (2)で求めた $V_n$ に対して，$\displaystyle\sum_{n=1}^\infty V_{2n-1}=V_1+V_3+V_5+\cdots$ を求めなさい。

$e^x\cos x$ の積分

そこで，逆方向から攻めてみます。つまり，微分して $e^{-2x}\cos 2x$ になる式というものを作れば，それが積分の答えになるはずです。

ここからは解法として暗記していきましょう。まず，$e^{-2x}\sin 2x$ を微分します。

$(e^{-2x}\sin 2x)’=(e^{-2x})’\sin2x+e^{-2x}(\sin2x)’$
$=-2e^{-2x}\sin2x+2e^{-2x}\cos2x$ ・・・①

次に，$e^{-2x}\sin 2x$ を微分します。こうして，$\sin$ と $\cos$ の式を微分したものを用意します。

$(e^{-2x}\cos2x)’=-2e^{-2x}\cos2x-2e^{-2x}\sin2x$ ・・・②

①と②を使ってジャマな右辺の $\sin$ を消去します。

$(e^{-2x}\sin2x-e^{-2x}\cos2x)’=4e^{-2x}\cos2x$
$\cfrac{1}{4}(e^{-2x}\sin2x-e^{-2x}\cos2x)’=e^{-2x}\cos2x$

したがって

$\displaystyle\int e^{-2x}\cos 2x\space dx=\cfrac{1}{4}(e^{-2x}\sin2x-e^{-2x}\cos2x)$
$=\cfrac{e^{-2x}}{4}(\sin2x-\cos2x)+C$　（$C$は積分定数）

（答え）

回転体の体積

(2)に進みます。

まずは，増減表を作ってグラフの概形を求めましょう。

$f(x)=e^{-x}\sin x$ として

$f'(x)=-e^{-x}\sin x+e^{-x}\cos x$
$=-e^{-x}(\sin x-\cos x)$

$-e^{-x}(\sin x-\cos x)=0$ とすると

$e^{-x}\not=0$ だから

$\sin x-\cos x=0$ とすると

三角関数の合成より

$\sqrt{2}\sin\Big(x-\cfrac{\pi}{4}\Big)=0$
$\sin\Big(x-\cfrac{\pi}{4}\Big)=0$
$x-\cfrac{\pi}{4}=0,\pi$

$(n-1)\pi\leqq x\leqq n\pi$ を考慮すると

$x=\cfrac{\pi}{4}+(n-1)\pi$　$(n=1,2,3,\cdots)$

増減表は

$\def\arraystretch{1.5}\begin{array}{|c|c|c|c|c|c|c|}\hline x&0&\cdots&\frac{\pi}{4}&\cdots&\pi&\cdots\\\hline f'(x)&+&+&0&-&-\\\hline f(x)&0&\nearrow&&\searrow&0\\\hline\end{array}$

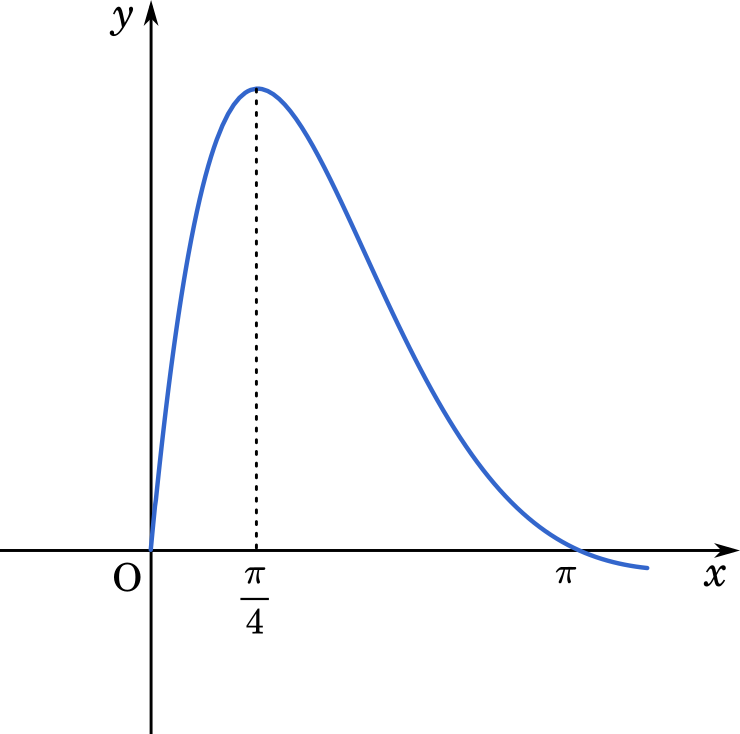
グラフはこのようになります。

$(n-1)\pi\leqq x\leqq n\pi$ より

$n=1$ のとき，$0\leqq x\leqq\pi$
$n=2$ のとき，$\pi\leqq x\leqq2\pi$

のようになるので，積分区間はグラフの山 1 つ分で考えれば良さそうです。

回転体の体積は，円の面積を積み重ねることで求められます。

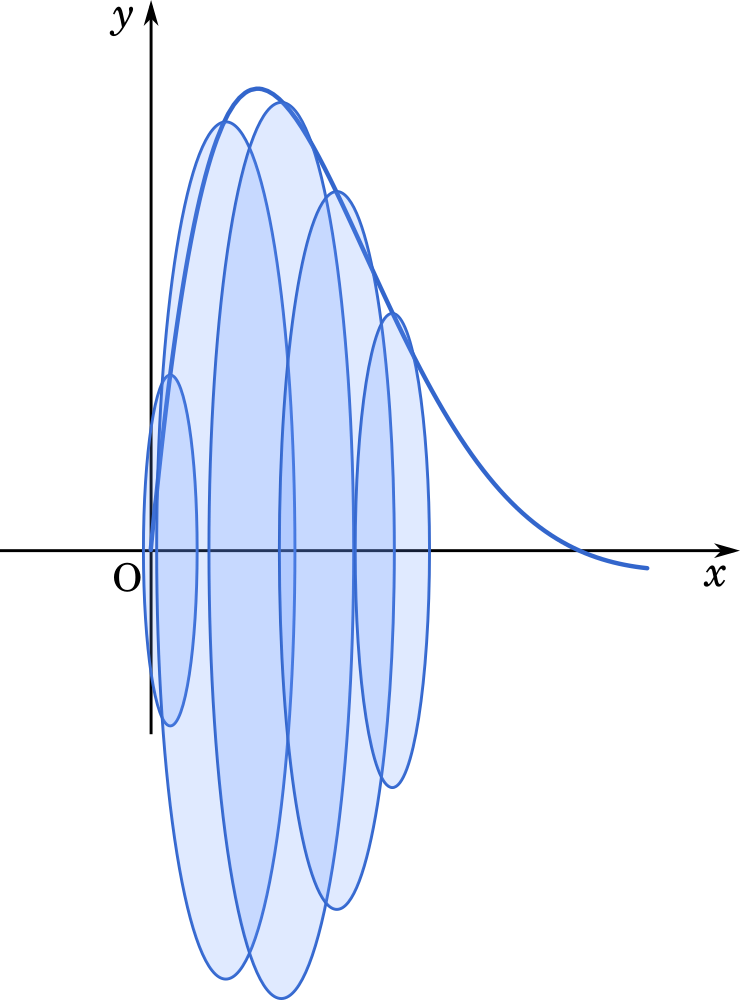
$\displaystyle V_n=\int_{\small{(n-1)\pi}}^{\small{n\pi}}\pi r^2\space dx$
$\displaystyle=\pi\int_{\small{(n-1)\pi}}^{\small{n\pi}}(e^{-x}\sin x)^2\space dx$
$\displaystyle=\pi\int_{\small{(n-1)\pi}}^{\small{n\pi}}e^{-2x}\sin^2 x\space dx$

積分式の中に $\sin^2$ の形ができたら，半角の公式を使って 2 乗を解消するのがセオリーです。

$\displaystyle=\pi\int_{\small{(n-1)\pi}}^{\small{n\pi}}e^{-2x}\cdot\cfrac{1-\cos2x}{2}\space dx$
$\displaystyle=\cfrac{\pi}{2}\Big\{\int_{\small{(n-1)\pi}}^{\small{n\pi}}e^{-2x}\space dx-\int_{\small{(n-1)\pi}}^{\small{n\pi}}e^{-2x}\cos2x\space dx\Big\}$

式を 2 つに分けてそれぞれ計算していきましょう。

$\displaystyle\int_{\small{(n-1)\pi}}^{\small{n\pi}}e^{-2x}\space dx$
$=\Big[-\cfrac{1}{2}e^{-2x}\Big]_{\small{(n-1)\pi}}^{\small{n\pi}}$
$=-\cfrac{1}{2}\{e^{-2n\pi}-e^{-2(n-1)\pi}\}$
$=-\cfrac{e^{-2n\pi}}{2}(1-e^{2\pi})$

また

$\displaystyle=\int_{\small{(n-1)\pi}}^{\small{n\pi}}e^{-2x}\cos2x\space dx$

(1)より

$\displaystyle=\cfrac{1}{4}\Big[e^{-2x}(\sin2x-\cos2x)\Big]_{\small{(n-1)\pi}}^{\small{n\pi}}$
$=\cfrac{1}{4}\{e^{-2n\pi}\cdot(-1)-e^{-2(n-1)\pi}\cdot(-1)\}$
$=\cfrac{1}{4}(-e^{-2n\pi}+e^{-2n\pi+2\pi})$
$=\cfrac{e^{-2n\pi}}{4}(e^{2\pi}-1)$

したがって

$V_n=\cfrac{\pi}{2}\Big\{-\cfrac{e^{-2n\pi}}{2}(1-e^{2\pi})-\cfrac{e^{-2n\pi}}{4}(e^{2\pi}-1)$
$=\cfrac{\pi}{8}e^{-2n\pi}\{-2(1-e^{2\pi})-(e^{2\pi}-1)\}$
$=\cfrac{\pi}{8}e^{-2n\pi}(e^{2\pi}-1)$　（答え）

等比数列を見つける

(3)に進みます。

$\displaystyle\sum_{n=1}^\infty V_{2n-1}=V_1+V_3+V_5+\cdots$

たとえば

$\cfrac{V_3}{V_1}=\cfrac{\cfrac{\pi}{8}e^{-6\pi}(e^{2\pi}-1)}{\cfrac{\pi}{8}e^{-2\pi}(e^{2\pi}-1)}$
$=\cfrac{}{}e^{-4\pi}$

$n$ の値を増やしても同じ結果になるはずです。つまり，この数列は公比 $e^{-4\pi}$ です。

ここで，等比数列の和を求めてみましょう。

$\cfrac{\cfrac{\pi}{8}e^{-2\pi}(e^{2\pi}-1)\{1-(e^{-4\pi})^n\}}{1-e^{-4\pi}}$

ここで，$n\rightarrow\infty$ とすると

$(e^{-4\pi})^n=\cfrac{1}{(e^{4\pi})^n}\rightarrow\cfrac{1}{\infty}=0$

となるので

$\displaystyle\sum_{n=1}^\infty V_{2n-1}=\cfrac{\cfrac{\pi}{8}e^{-2\pi}(e^{2\pi}-1)}{1-e^{-4\pi}}$

式をもう少し整理しましょう。

$=\cfrac{\pi}{8}\cdot\cfrac{1-e^{-2\pi}}{1-e^{-4\pi}}$
$=\cfrac{\pi(1-e^{-2\pi})(1+e^{-2\pi})}{8(1-e^{-4\pi})(1+e^{-2\pi})}$
$=\cfrac{\pi(1-e^{-4\pi})}{8(1-e^{-4\pi})(1+e^{-2\pi})}$
$=\cfrac{\pi}{8(1+e^{-2\pi})}$　（答え）