【空間ベクトル・積分】円錐を斜めに切った断面の面積(神戸大2018理系第5問)

座標空間において，O を原点とし，A $(2,0,0)$，B $(0,2,0)$，C $(1,1,0)$ とする。△OAB を直線 OC の周りに 1 回転してできる回転体を $L$ とする。以下の問に答えよ。

(1) 直線 OC 上にない点 P $(x,y,z)$ から直線 OC におろした垂線を PH とする。 $\overrightarrow{\text{OH}}$ と $\overrightarrow{\text{HP}}$ を $x,y,z$ の式で表わせ。

(2) 点 P $(x,y,z)$ が $L$ の点であるための条件は

$z^2\leqq2xy$ かつ $0\leqq x+y\leqq2$

であることを示せ。

(3) $1\leqq a\leqq2$ とする。$L$ を平面 $x=a$ で切った切り口の面積 $S(a)$ を求めよ。

(4) 立体 $\{(x,y,z)|(x,y,z)\in L,1\leqq x\leqq2\}$ の体積を求めよ。

内積 0 を利用する

(1)から始めます。

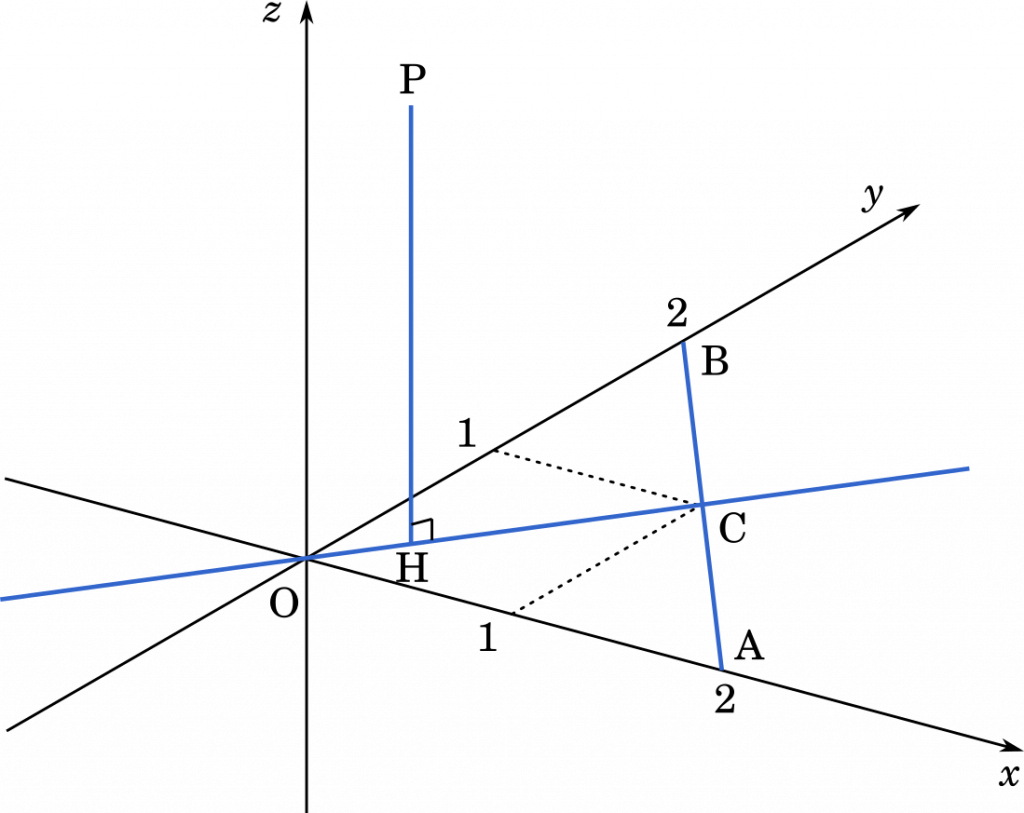
点 H は直線 OC 上の点なので，$k$ を用いて

$\overrightarrow{\text{OH}}=k(1,1,0)$
$=(k,k,0)$

と表すことができます。よって

$\overrightarrow{\text{HP}}=\overrightarrow{\text{OP}}-\overrightarrow{\text{OH}}$
$=(x,y,z)-(k,k,0)$
$=(x-k,y-k,z)$

また，OH と OC は垂直の関係にあるので，その内積は 0 になります。

$\overrightarrow{\text{HP}}\cdot\overrightarrow{\text{OC}}=x-k+y-k+z\cdot0=0$
$x-k+y-k=0$

$x-y-2k=0$

$k=\cfrac{x+y}{2}$

したがって

$\overrightarrow{\text{OH}}=\Big(\cfrac{x+y}{2},\cfrac{x+y}{2},0\Big)$
$\overrightarrow{\text{HP}}=\Big(\cfrac{x-y}{2},\cfrac{y-x}{2},z\Big)$　（答え）

回転体上の点

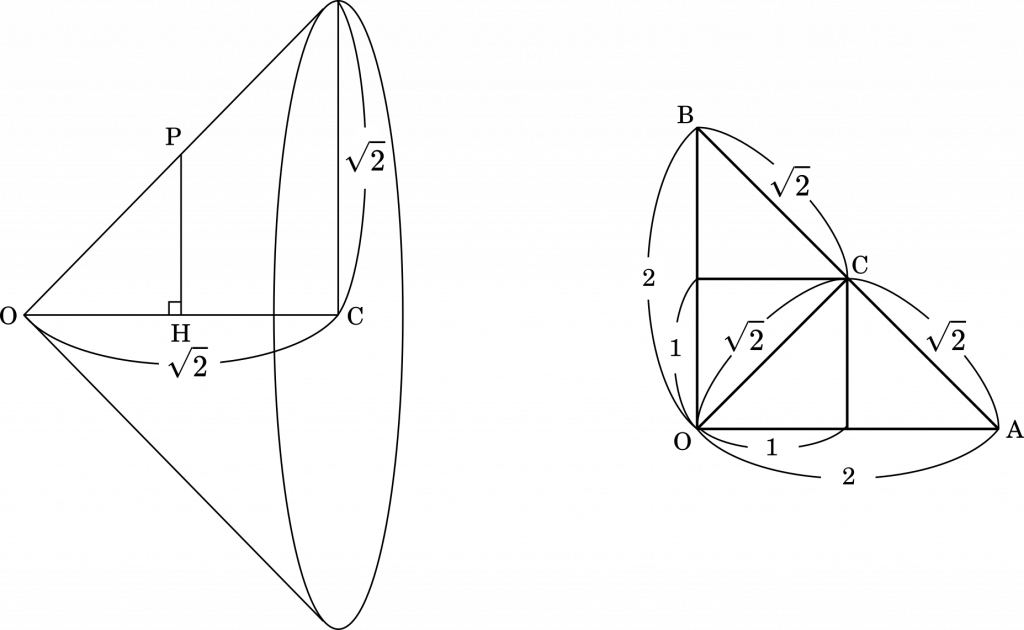
図を描いてみると，点 P が回転体の周または内部の点であるための条件がみえてきます。

$\begin{cases}x\geqq0\\y\geqq0\\0\leqq k\leqq1\\0\leqq|\overrightarrow{\text{OH}}|\leqq\sqrt{2}\\0\leqq|\overrightarrow{\text{PH}}|\leqq\sqrt{2}\\|\overrightarrow{\text{PH}}|\leqq|\overrightarrow{\text{OH}}|\end{cases}$

$|\overrightarrow{\text{OH}}|^2=\Big(\cfrac{x+y}{2}\Big)^2+\Big(\cfrac{x+y}{2}\Big)^2$
$=\cfrac{(x+y)^2}{2}\leqq2$
$(x+y)^2\leqq4$

よって

$0\leqq x+y\leqq2$

さらに

$|\overrightarrow{\text{PH}}|^2=\Big(\cfrac{x-y}{2}\Big)^2+\Big(\cfrac{y-x}{2}\Big)^2+z^2$
$=\cfrac{x^2-2xy+y^2+y^2-2xy+x^2}{4}+z^2$
$=\cfrac{2(x^2-2xy+y^2)}{4}+z^2$
$=\cfrac{(x-y)^2}{2}+z^2\leqq2$

よって

$|\overrightarrow{\text{PH}}|\leqq|\overrightarrow{\text{OH}}|$ より

$|\overrightarrow{\text{PH}}|^2\leqq|\overrightarrow{\text{OH}}|^2$

$\cfrac{(x-y)^2}{2}+z^2\leqq\cfrac{(x+y)^2}{2}$
$z^2\leqq\cfrac{(x+y)^2-(x-y)^2}{2}$
$z^2\leqq\cfrac{x^2+2xy+y^2-x^2+2xy-y^2}{2}$
$z^2\leqq\cfrac{4xy}{2}$
$z^2\leqq2xy$　（証明終わり）

切断面の面積

(3)に進みます。

平面で切った切り口は回転体の周または内部の点です。そこで(2)で証明した不等式を利用します。

$x=a$ とすると

$z^2\leqq2ay$
$\cfrac{z^2}{2a}\leqq y$ ・・・①

$a$ は定数だから，$y$ と $z$ の関係を表すことができました。

また

$0\leqq a+y\leqq2$
$0\leqq y\leqq2-a$ ・・・②

①，②より

$\cfrac{z^2}{2a}\leqq y\leqq2-a$

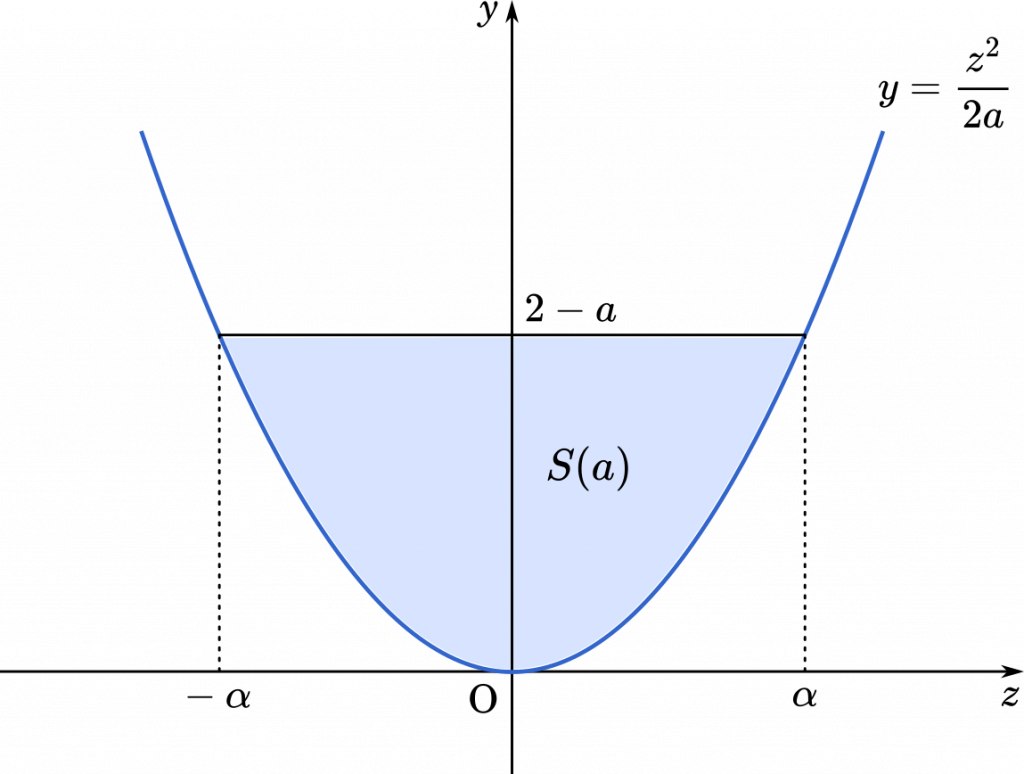
$y=2-a$ と $y=\cfrac{z^2}{2a}$ の交点の $z$ 座標を $\alpha,-\alpha$ としておきます。

面積は 6 分の 1 公式を使って求めましょう。

$S(a)=\cfrac{\Big|\cfrac{1}{2a}\Big|\{\alpha-(-\alpha)\}^3}{6}$
$=\cfrac{8\alpha^3}{12a}$
$=\cfrac{2}{3a}\alpha^3$

ここで，$\alpha$ を求めると

$2-a=\cfrac{z^2}{2a}$
$z^2=2a(2-a)$
$z=\pm\sqrt{2a(2-a)}$

よって，$\alpha=\sqrt{2a(2-a)}$ です。

$S(a)=\cfrac{2}{3a}\cdot2a(2-a)\sqrt{2a(2-a)}$
$=\cfrac{4(2-a)}{3}\sqrt{2a(2-a)}$　（答え）

体積を求める

(4)に進みます。

$\displaystyle V=\int_1^2\cfrac{4(2-a)}{3}\sqrt{2a(2-a)}\space da$

定数を前に出しておきます。

$\displaystyle=\cfrac{4\sqrt{2}}{3}\int_1^2(2-a)\sqrt{a(2-a)}\space da$

ルートの中を展開すると $2a-a^2$ となります。方針としては，ルートの中に 2 次関数が出てきたらいったん平方完成してみると良いでしょう。

平方完成して

$\displaystyle=\cfrac{4\sqrt{2}}{3}\int_1^2(2-a)\sqrt{1-(a-1)^2}\space da$

ここで，$a-1=\sin\theta$ とすると

$da=\cos\theta\space d\theta$

$\def\arraystretch{1.5}\begin{array}{c|c}a&1\rightarrow2\\\hline\theta&0\rightarrow\frac{\pi}{2}\end{array}$

また，$a=1+\sin\theta$ だから

$\displaystyle=\cfrac{4\sqrt{2}}{3}\int_0^\frac{\pi}{2}(2-1-\sin\theta)\sqrt{1-\sin^2\theta}\cdot\cos\theta\space d\theta$

$\displaystyle=\cfrac{4\sqrt{2}}{3}\int_0^\frac{\pi}{2}(1-\sin\theta)\cos^2\theta\space d\theta$

$\displaystyle=\cfrac{4\sqrt{2}}{3}\int_0^\frac{\pi}{2}\cos^2\theta-\sin\theta\cos^2\theta\space d\theta$

$\displaystyle=\cfrac{4\sqrt{2}}{3}\int_0^\frac{\pi}{2}\cfrac{1+\cos2\theta}{2}-\sin\theta\cos^2\theta\space d\theta$

$=\cfrac{2\sqrt{2}}{3}\Big[\theta-\cfrac{1}{2}\sin2\theta\Big]_0^\frac{\pi}{2}+\cfrac{4\sqrt{2}}{3}\Big[\cfrac{1}{3}\cos^3\theta\Big]_0^\frac{\pi}{2}$
$=\cfrac{2\sqrt{2}}{3}\cdot\cfrac{\pi}{2}-\cfrac{4\sqrt{2}}{9}$
$=\cfrac{\sqrt{2}\pi}{3}-\cfrac{4\sqrt{2}}{9}$　（答え）