【数III積分】円柱を斜めに切った体積とドーナツ回転体(断面が台形)(九州大)

座標空間において，中心 (0, 2, 0)，半径 1 で $xy$ 平面内にある円を $D$ とする。$D$ を底面とし，$z$ ≧ 0 の部分にある高さ 3 の直円柱(内部を含む)を$E$ とする。点 (0, 2, 2) と $x$ 軸を含む平面で $E$ を 2 つの立体に分け，$D$ を含む方を $T$ とする。以下の問いに答えよ。(九州大2020)

(1) －1 ≦ $t$ ≦ 1 とする。平面 $x=t$ で $T$ を切ったときの断面積 $S(t)$ を求めよ。また，$T$ の体積を求めよ。

(2) $T$ を $x$ 軸のまわりに 1 回転させてできる立体の体積を求めよ。

---

円を原点に移動する

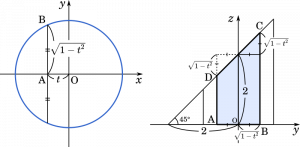
$x^2+y^2=1$

$y^2=1-x^2$

$y=\pm\sqrt{1-x^2}$

$x=t$ のとき

$y=\pm\sqrt{1-t^2}$

AD ＝ $2-\sqrt{1-t^2}$

BC ＝ $2+\sqrt{1-t^2}$

よって

AD＋BC ＝ $2-\sqrt{1-t^2}+2+\sqrt{1-t^2}=4$

また，高さ AB は $2\sqrt{1-t^2}$ となる。

台形 ABCD の面積は

$S(t)=\cfrac{1}{2}\cdot 2\sqrt{1-t^2}\cdot4$

$=4\sqrt{1-t^2}$　(答え)

置換積分と半角の公式を用いて積分する

$\displaystyle V=\int_{-1}^1 4\sqrt{1-t^2}\space dt$

立体は左右対称だから

$\displaystyle=2\int_0^1 4\sqrt{1-t^2}\space dt$

$\displaystyle=8\int_0^1\sqrt{1-t^2}\space dt$

$t=\sin\theta$ とおくと

$dt=\cos\theta\space d\theta$

$\def\arraystretch{1.25}\begin{array}{c:c} t & 0\rightarrow 1\\\hline \theta & 0\rightarrow\cfrac{\pi}{2}\end{array}$

したがって

$\displaystyle V=8\int_{\small{0}}^{\small{\cfrac{\pi}{2}}}\sqrt{1-\sin^2\theta}\cos\theta\space d\theta$

$\displaystyle=8\int_{\small{0}}^{\small{\cfrac{\pi}{2}}}\cos^2\theta\space d\theta$

$\displaystyle=8\int_{\small{0}}^{\small{\cfrac{\pi}{2}}}\cfrac{1+\cos2\theta}{2}\space d\theta$

$\displaystyle=4\int_{\small{0}}^{\small{\cfrac{\pi}{2}}}1+\cos2\theta\space d\theta$

$=4\Big[\theta-\cfrac{1}{2}\sin2\theta\Big]_{\small{0}}^{\small{\cfrac{\pi}{2}}}$

$=4\Big(\cfrac{\pi}{2}-\cfrac{1}{2}\sin\pi\Big)$

$=2\pi$　(答え)

ドーナツ型の回転体の体積

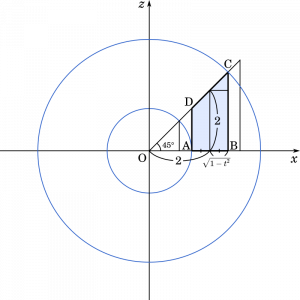
OC ＝ $\sqrt{2}(2+\sqrt{1-t^2})$

OA ＝ $2-\sqrt{1-t^2}$

$S=\pi\{\sqrt{2}(2+\sqrt{1-t^2})\}^2-\pi(2-\sqrt{1-t^2})^2$

$=\pi\{(2\sqrt{2}+\sqrt{2}\cdot\sqrt{1-t^2})^2-(2-\sqrt{1-t^2})^2\}$

$=\pi\{8+8\sqrt{1-t^2}+2(1-t^2)-4+4\sqrt{1-t^2}-(1-t^2)\}$

$=\pi(4+12\sqrt{1-t^2}+1-t^2)$

$=\pi(5-t^2+12\sqrt{1-t^2})$

前の積分の結果を利用する

$\displaystyle V=2\pi\int_0^1 5-t^2+12\sqrt{1-t^2}\space dt$

$\displaystyle 8\int_0^1 \sqrt{1-t^2}\space dt=2\pi$ より

$\displaystyle \int_0^1 \sqrt{1-t^2}\space dt=\cfrac{\pi}{4}$

これを用いて

$\displaystyle V=2\pi\int_0^1 5-t^2+12\sqrt{1-t^2}\space dt$

$\displaystyle =2\pi\int_0^1 5-t^2\space dt+2\pi\cdot12\cdot\cfrac{\pi}{4}$

$=2\pi\Big[5t-\cfrac{t^3}{3}\Big]_0^1+6\pi^2$

$=2\pi\Big(5-\cfrac{1}{3}\Big)+6\pi^2$

$=2\pi\cdot\cfrac{14}{3}+6\pi^2$

$=\cfrac{28}{3}\pi+6\pi^2$ (答え)