「その文字は何番目に来るのか」で考える―C の意味を超基本に戻っておさらい(東京都立大2017文系第2問)

あとの実戦問題に合わせて，例を考えてみましょう。

[問題] A か B の文字を 2 個並べるとする。このとき，AA となるのは何通りか。

[問題] A か B の文字を 3 個並べるとする。このとき，A が 2 個となるのは何通りか。

これは，AAB，ABA，BAA の 3 通りとなります。

このように数が少ないときには単に数えればよいのですが，文字数が増えると大変です。

ここから発想を切り替えましょう。

1 番目に A が来るか B が来るかではなく，2 つの A が何番目と何番目に来るかを考えることにします。これは樹形図で考えることができます。

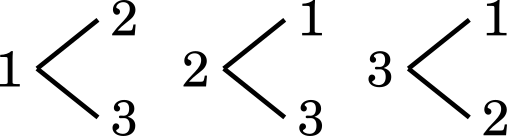
このとき，1 → 2 番目と 2 → 1 番目は同じことなので，1 通りとして数えます。同じように 1 → 3 と 3 → 1 ，2 → 3 と 3 → 2 も 1 通りとして数えるので，結局 3 通りになります。

このように，1 → 2 があるときには必ず 2 → 1 もあるので，2 で割ればよいことになります。
$\cfrac{3\times2}{2}=_3C_2$
これは，$_3C_2$ として表すことができます。

文字を並べる問題では，A が何番目と何番目に来るかを考えます。つまり，1 ～ 3 番目から 2 つを選ぶ問題と考えることで答えを出せるのです。

実戦問題

2 個の文字 A，B を重複を許して左から並べて 7 文字の順列を作る。次の条件をみたす順列はそれぞれいくつあるか答えなさい。（東京都立大2017）
(1) A が 5 個以上現れる。
(2) AABB がこの順に連続して現れる。
(3) A が 3 個以上連続して現れる。

場合分けをする

(1)から始めます。
(i) A が 5 個のとき
上でやったように，A が何番目と何番目に来るかを考えます。つまり「1 ～ 7 番目から 5 つを選ぶ問題」として考えれば良いことになります。
$_7C_5=_7C_2=\cfrac{7\cdot6}{2}=21$
(ii) A が 6 個のとき
$_7C_6=_7C_1=7$
(iii) A が 7 個のとき
$_7C_7=1$
したがって
$21+7+1=29$　（答え）

かたまりを 1 つとして考える

(2)に進みます。

○ (AABB) ○ ○

AABBを一つのかたまりとして考えましょう。AABB を 1 つの文字とすると，全体が 4 文字の並べかえとして見ることができます。
(AABB)のかたまりは 1 ～ 4 番目のいずれかだから 4 通りです。そして，残りの 3 文字は A か B のいずれかだから，$2\times2\times2$ 通りの組み合わせを作ることができます。
$4\times2^3=32$　（答え）

複雑な場合分け

(3)に進みます。これも場合分けをしていきます。
(i) A が 3 個連続
AAAB○○○　8 通り
BAAAB○○　4 通り
○BAAAB○　4 通り
○○BAAAB　4 通り
○○○BAAA　8 通り
AAAが3個連続するとき，その隣はBでなければ3個だけ連続になりません。

○の部分はAのときとBのときがあるので，○が2つなら $2^2=4$ 通り，○が3つなら $2^3=8$ 通りとなります。

ここは注意深さの問題です。AAAB○○○ には AAABAAA が含まれますが，○○○BAAA にも AAABAAA が含まれます。つまり，これだけが重複するのです。よって
$8+4+4+4+8-1=27$ 通り
となります。
(ii) A が 4 個連続
AAAAB○○　4 通り
BAAAAB○　2 通り
○BAAAAB　2 通り
○○BAAAA　4 通り
$4+2+2+4=12$ 通り
(iii) A が 5 個連続
AAAAAB○　2 通り
BAAAAAB　1 通り
○BAAAAA　2 通り
$2+1+2=5$ 通り
(iv) A が 6 個連続
AAAAAAB
BAAAAAA
2 通り
(v) A が 7 個連続
AAAAAAA
1 通り
したがって
$27+12+5+2+1=47$　（答え）
一か所だけトラップがありますが，それ以外はスムーズに組み合わせを作ることができるはずです。○に入る文字を具体的にイメージして，見逃しがないようにしましょう。