【数IIBベクトル/数III放物線】直線に下ろした垂線との交点／放物線の焦点と準線を求める(北海道大2016理系第5問)

空間の 2 点 A$(0,0,2)$，B$(0,1,3)$ を通る直線 $\ell$ とし，2 点 C$(1,0,0)$，D$(1,0,1)$ を通る直線 $m$ とする。$a$ を定数として，$\ell$ 上にも $m$ 上にもない点 P$(s,t,a)$ を考える。(北海道大2016)

(1) P から $\ell$ の下ろした垂線と $\ell$ の交点を Q とし，P から $m$ に下ろした垂線と $m$ の交点を $R$ とする。Q，R の座標をそれぞれ $s,t,a$ を用いて表せ。

(2) P を中心とし，$\ell$ と $m$ がともに接するような球面が存在するための条件を $s,t,a$ の関係式で表せ。

(3) $s,t$ と定数 $a$ が(2)の条件をみたすとき，平面上の点 $(s,t)$ の軌跡が放物線であることを示し，その焦点と純線を $a$ を用いて表せ。

内積を利用して垂線との交点を求める

(1)から考えます。

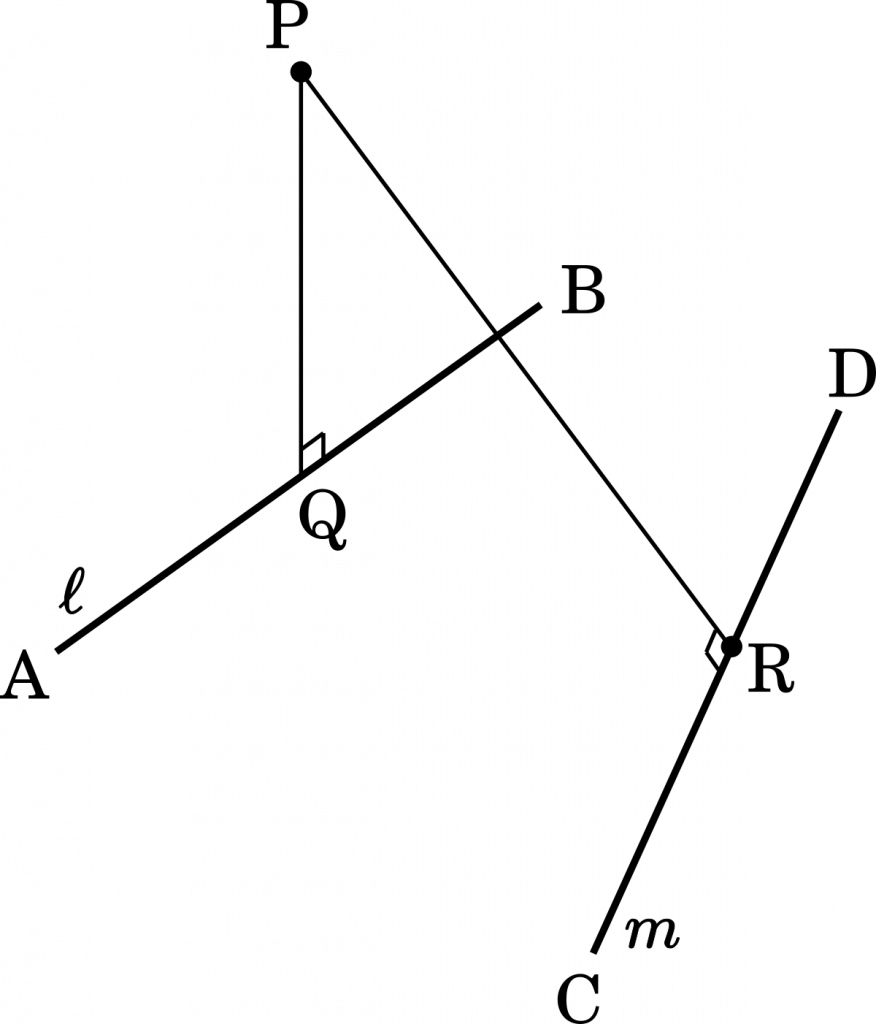
各点の座標はあまり考えずに，とりあえずの図で構いません。

直角があるので，内積を使うことになります。

$\overrightarrow{\text{AB}}=(0,1,3)-(0,0,2)$
$=(0,1,1)$

また

$\overrightarrow{\text{PQ}}=\overrightarrow{\text{AQ}}-\overrightarrow{\text{AP}}$

となります。$\overrightarrow{\text{AQ}}$ と $\overrightarrow{\text{AP}}$ を求めます。

$\overrightarrow{\text{AQ}}=k\overrightarrow{\text{AB}}$ ($k$は実数) として

$=k\{(0,1,3)-(0,0,2)\}$
$=k(0,1,1)$
$=(0,k,k)$ ・・・①

また

$\overrightarrow{\text{AP}}=(s,t,a)-(0,0,2)$
$=(s,t,a-2)$

よって

$\overrightarrow{\text{PQ}}=\overrightarrow{\text{AQ}}-\overrightarrow{\text{AP}}$
$=(0,k,k)-(s,t,a-2)$
$=(-s,k-t,k-a+2)$

$\overrightarrow{\text{AB}}\cdot\overrightarrow{\text{PQ}}=0$ より
$(0,1,1)\cdot(-s,k-t,k-a+2)=0$
$k-t+k-a+2=0$
$2k-a-t+2=0$
$2k=a+t-2$
$k=\cfrac{t+a-2}{2}$

①に代入して

$\overrightarrow{\text{AQ}}=\Big(0,\cfrac{t+a-2}{2},\cfrac{t+a-2}{2}\Big)$

これはまだ答えではありません。点 Q の座標は原点を始点として考えなければならないので，求めるのは $\overrightarrow{\text{AQ}}$ ではなく $\overrightarrow{\text{OQ}}$ です。

$\overrightarrow{\text{AQ}}=\overrightarrow{\text{OQ}}-\overrightarrow{\text{OA}}$ より
$\overrightarrow{\text{OQ}}=\overrightarrow{\text{AQ}}+\overrightarrow{\text{OA}}$
$=\Big(0,\cfrac{t+a-2}{2},\cfrac{t+a-2}{2}\Big)+(0,0,2)$
$=\Big(0,\cfrac{t+a-2}{2},\cfrac{t+a+2}{2}\Big)$ (答え)

点 R の座標も同じようにして求められます。

$\overrightarrow{\text{CD}}=(1,0,1)-(1,0,0)=(0,0,1)$

$\overrightarrow{\text{PR}}=\overrightarrow{\text{CR}}-\overrightarrow{\text{CP}}$ となるので
$\overrightarrow{\text{CR}}=k\overrightarrow{\text{CD}}$ として
$=k(0,0,1)=(0,0,k)$ ・・・②

$\overrightarrow{\text{CP}}=(s,t,a)-(1,0,0)$
$=(s-1,t,a)$

よって

$\overrightarrow{\text{PR}}=\overrightarrow{\text{CR}}-\overrightarrow{\text{CP}}$
$=(0,0,k)-(s-1,t,a)$
$=(-s+1,-t,k-a)$

$\overrightarrow{\text{CD}}\cdot\overrightarrow{\text{PR}}=0$ より
$(0,0,1)\cdot(-s+1,-t,k-a)=0$
$k-a=0$
$k=a$

②に代入して

$\overrightarrow{\text{CR}}=(0,0,a)$

$\overrightarrow{\text{CR}}=\overrightarrow{\text{OR}}-\overrightarrow{\text{OC}}$ より

$\overrightarrow{\text{OR}}=\overrightarrow{\text{CR}}+\overrightarrow{\text{OC}}$
$=(0,0,a)+(1,0,0)$
$=(1,0,a)$ (答え)

２乗して絶対値を外す

(2)に進みます。

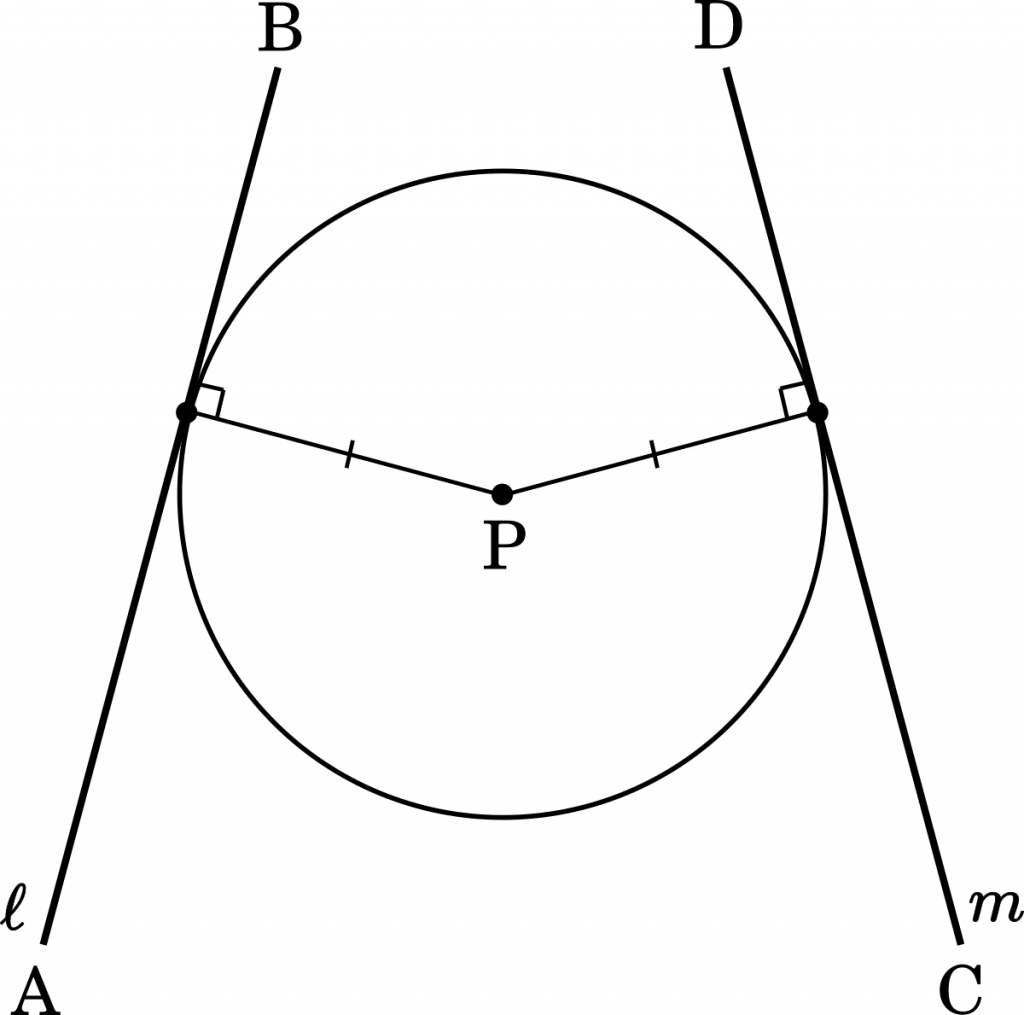
上の図より，$|\overrightarrow{\text{PQ}}|=|\overrightarrow{\text{PR}}|$ の関係が成り立つことが分かります。

ゴール地点がいまいち見えないかもしれませんが，とりあえずこれを使って式を作っていきましょう。

$\overrightarrow{\text{PQ}}=\Big(0,\cfrac{t+a-2}{2},\cfrac{t+a+2}{2}\Big)-(s,t,a)$
$=\Big(-s,\cfrac{-t+a-2}{2},\cfrac{t-a+2}{2}\Big)$

また

$\overrightarrow{\text{PR}}=(1,0,a)-(s,t,a)$
$=(1-s,-t,0)$

このままだと話が進まないので，２乗して絶対値を外します。

$|\overrightarrow{\text{PQ}}|^2=|\overrightarrow{\text{PR}}|^2$ を求める。

$|\overrightarrow{\text{PQ}}|^2=\overrightarrow{\text{PQ}}\cdot\overrightarrow{\text{PQ}}$，$|\overrightarrow{\text{PR}}|^2=\overrightarrow{\text{PR}}\cdot\overrightarrow{\text{PR}}$ だから，内積の公式を用いて

$(-s)^2+\Big(\cfrac{-t+a-2}{2}\Big)^2+\Big(\cfrac{t-a+2}{2}\Big)^2=(1-s)^2+(-t)^2$

あとは，式を整理していけば関係式が作れそうです。

$s^2+\cfrac{(-t+a-2)^2}{4}+\cfrac{(t-a+2)^2}{4}=(1-s)^2+t^2$

両辺を 4 倍して

$4s^2+(-t+a-2)^2+(t-a+2)^2=4(1-s)^2+4t^2$
$4s^2+t^2+a^2+4-2at-4a+4t+t^2+a^2+4-2at-4a+4t=4-8s+4s^2+4t^2$
$-2t^2+2a^2-4at+8s+8t-8a+4=0$
$t^2+2at-4t-4s-a^2+4a-2=0$
$t^2+2(a-2)t-4s-a^2+4a-2=0$ (答え)

放物線を平行移動させた式

(3)に進みます。

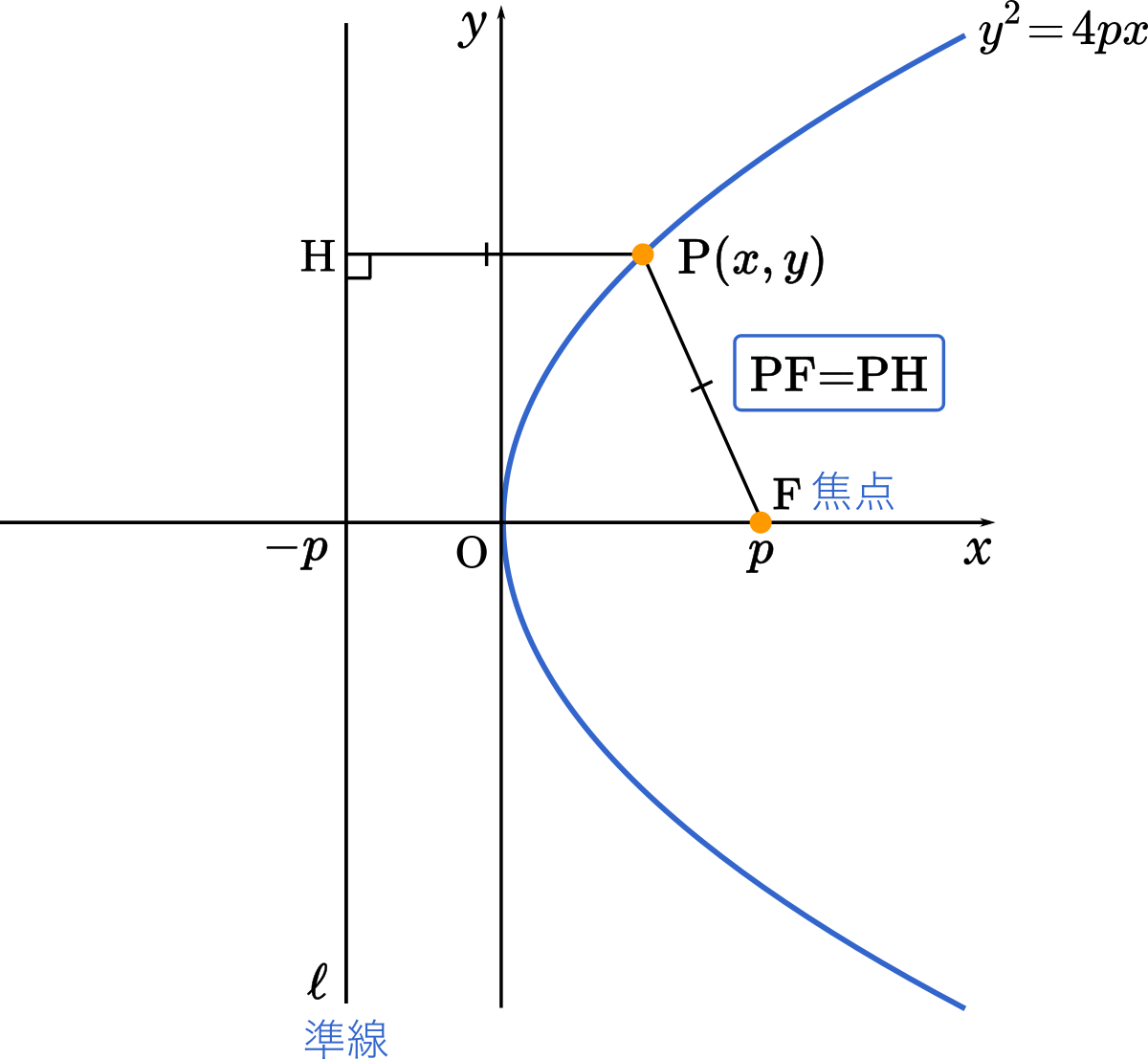
式を $y^2=4px$ の形に変形すれば良いのですが，(2)の答えを変形してもこの形にはなりそうにありません。

ここからは応用ですが，放物線を $x$ 軸方向に $X$，$y$ 軸方向に $Y$ 平行移動した式はこうなります。

$(y-Y)^2=4p(x-X)$

式をこの形に変形してみます。方針としては，(2)の式は $t$ の二次式と言えるので，$t$ を左辺にまとめていくと良いでしょう。つまり，左辺の $y^2$ を $t^2$ に置き換えるということです。

(2)より

$t^2+2(a-2)t-4s-a^2+4a-2=0$
$t^2+2(a-2)t=4s+a^2-4a+2$

左辺を平方完成して

$\{t+(a-2)\}^2-(a-2)^2=4s+a^2-4a+2$
$(t+a-2)^2=4s+a^2-4a+2+(a-2)^2$
$=4s+a^2-4a+2+a^2-4a+4$
$=4s+2a^2-8a+6$
$=4\Big(s+\cfrac{a^2-4a+3}{2}\Big)$

これは，$y^2=4px$ を $p=1$ として $t^2=4s$ に置き換え，$s$ 軸方向に $-\dfrac{a^2-4a+3}{2}$，$t$ 軸方向に $-a+2$ だけ平行移動した放物線であると言えます。

$p=1$ であることに注意すると，焦点は $(1,0)$ を平行移動したものだから

$\Big(1-\dfrac{a^2-4a+3}{2},-a+2\Big)$
$=\Big(-\cfrac{a^2}{2}+2a-\cfrac{1}{2},-a+2\Big)$ (答え)

また，準線は $s=-1$ を平行移動したものだから

$s=-1-\dfrac{a^2-4a+3}{2}$
$=-\cfrac{a^2}{2}+2a-\cfrac{5}{2}$ (答え)